Первое начало термодинамики и изопроцессы

3.5.1.Изохорный процесс (V = const)

Диаграмма изохорного процесса (изохора) в координатах p-V изображается прямой, параллельной оси p (рис.3) (процесс 1®2 отражает изохорное нагревание, а процесс 1®3 отражает изохорное охлаждение). При изохорном процессе газ не совершает работы над внешними телами dA = pdV = 0 и вся теплота, сообщаемая газу (или отбираемая от газа), идет на увеличение (уменьшение) его внутренней энергии, так что первое начало имеет вид dQ = dU = (m/M)C_VdT или для 1 моль dU_m = C_VdT.

3.5.2.Изобарный процесс (p = const)

Диаграмма изобарного процесса (изобара)в координатах p-V изображается прямой, параллельной оси V (рис.4). На рис.4. процесс 1®2 отражает изобарическое нагревание (объем газа увеличивается), а процесс 1®3 отражает изобарическое охлаждение (объем газа уменьшается). Изобарный процесс реализуется в сосуде с подвижным поршнем, на который действует постоянное внешнее давление.

При изобарном процессе расширения 1®2 объем газа увеличивается от V₁ до V₂ и газ совершает работу A₁₂ = 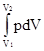= p(V₂ - V₁), величина этой работы определяется площадью светло-закрашенного прямоугольника на рис.4.

Если V₁ и V₂ выразить через уравнение Клапейрона-Менделеева [pV=(m/M)RT], то получим другое выражение для работы изобарного расширения A₁₂ = (m/M)R(T₂ - T₁), которое позволяет определить физический смысл молярной газовой постоянной R: она численно равна работе изобарного расширения 1 моль идеального газа при нагревании его на 1 К.

p p

3 1 2

o1

3 Рис.3. A₁₃ A₁₂ Рис.4.

V V

V₃ V₁ V₂

При изобарном нагревании газа 1®2 поступаемая теплота идет на возрастание внутренней энергии и совершение работы расширения газа (т.к. постоянство давления обеспечивается увеличением объема газа). При изобарном охлаждении 1®3 от газа отбирается теплота и это приводит к уменьшению его внутренней энергии, причем часть отбираемой теплоты идет на совершение работы по сжатию газа (т.к. постоянство давления обеспечивается уменьшением объема газа). Если газу массы m в изобарном процессе сообщить (отобрать) количество теплоты dQ = (m/M)C_pdT, то его внутренняя энергия возрастет (уменьшится) на величину dU = (m/M)C_VdT,и газ совершит работу (над газом будет совершена работа) A₁₂ = (m/M)R(T₂ - T₁), A₁₃ = (m/M)R(T₃ - Т₁), работа A₁₂ показана на рис.4 светло-закрашенным прямоугольником (она положительная, т.к. совершается газом над внешними силами), а работа A₁₃ показана на рис.4 темнозакрашенным прямоугольником (она отрицательная, т.к. совершается внешними силами над газом).

3.5.3.Изотермический процесс (T = const)

Изотермический процесс описывается законом Бойля-Мариотта (pV = const), диаграмма этого процесса (изотерма) в координатах p-V представляет собой гиперболу (рис.5). На рис.5 процесс 1®2 отражает изотермическое расширение газа, а процесс 1®3 отражает изотермическое сжатие газа. Изотермическими являются процессы кипения, плавления, конденсации, происходящие при постоянном внешнем давлении.

При T = const внутренняя энергия системы не изменяется dU = (m/M)C_VdT = 0 и первое начало запишется dQ = dA, т.е. вся теплота, сообщаемая газу, расходуется на совершение им работы против внешних сил.

Работа изотермического расширения

Q = A₁₂ = (m/M)RTln(V₂/V₁) = (m/M)RTln(p₁/p₂),

где использован закон Клапейрона-Менделеева[pV = (m/M)RT].

Если газ изотермически расширяется в процессе 1®2 (V₂ > V₁), то к нему подводится тепло (Q>0) и газ совершает работу над внешними силами (A₁₂>0). Графически эта работа измеряется площадью светло-закрашенной фигуры на рис.5 При изотермическом сжатии в процессе 1®3 (V₁ > V₂) от газа отводится тепло (Q < 0) и над газом внешние силы совершают работу (А₁₃< 0). Графически эта работа измеряется темнозакрашенной фигуры на рис.5.

p p p

dQ=0

3

Рис.5. Рис.6. Рис.7.

3 1 2

T=const

13 1 2

A₁₃ A₁₂2

A₁₃ A₁₂

V V V

V₃ V₁ V₂ V₃V₁V₂

3.5.4. Адиабатический процесс (dQ = 0)

Адиабатический процесс - это процесс, при котором отсутствует теплообмен (dQ=0) между системой и окружающей средой. Адиабатическими являются все быстропротекающие процессы (процесс распространения звука в среде - скорость звука столь велика, что обмен энергией между волной и средой не успевает происходить; процесс расширения и сжатия горючей смеси в цилиндрах двигателя внутреннего сгорания - скорость сжатия (расширения) столь велика, что обмен энергией между смесью и средой не успевает происходить).

Первое начало для адиабатического процесса dA =-dU, т.е. при адиабатическом процессе работа совершается за счет изменения внутренней энергии системы: если газ совершает работу над внешними силами, то его внутренняя энергия уменьшается, если над газом внешние силы совершают работу, то его внутренняя энергия увеличивается.

Для произвольной массы газа pdV = -(m/M)C_VdT. (*)

Продифференцировав уравнение Клапейрона-Менделеева pV=(m/M)RT, получим pdV + Vdp = (m/M)RdT, и использовав соотношение C_p - C_V = R, получим из двух последних уравнений dp/p =-gdV/V, где g = C_p/C_V. Интегрируя это уравнение , получим p₂/p₁ = (V₁/V₂)^g или p₁V₁^g = p₂V₂^g . Таким образом, получим уравнение адиабатического процесса (уравнение Пуассона)pV^g = const, где величина g = (i+2)/i называется показателем адиабаты (коэффициент Пуассона).

Для одноатомных газов (i=3) g = 1.67, для двухатомных газов (i=5) g = 1.4. Теоретические значения g хорошо подтверждаются в эксперименте. Диаграмма адиабатического процесса в координатах p-V (адиабата) представляет собой гиперболу (рис.6,7): процесс 1®2 на рис.7 демонстрирует адиабатическое расширение, а процесс 1®3 - адиабатическое сжатие.

Используя уравнение Клапейрона-Менделеева, уравнение Пуассона для адиабатического процесса можно записать TV^g-1 = const, T^g p^1-g = const.

На рис.6 показаны адиабата и изотерма процессов, отвечающих общему начальному состоянию газа 1: видно, что при адиабатическом процессе давление изменяется с изменением объема резче, чем при изотермическом процессе. При адиабатическом расширении (сжатии) газа уменьшается (увеличивается) его температура и это объясняет более резкое падение (возрастание) давления по сравнению с изотермическим расширением.

Выражение для работы при адиабатическом процессе может быть получено путем интегрирования уравнения (*) с учетом того, что когда газ адиабатически расширяется (процесс 1®2 на рис.7) от V₁ до V₂, его температура понижается от Т₁ до Т₂: A₁₂ = [p₁V₁/(g-1)][1-(V₁/V₂)^g-1] = [(m/M)RT₁/(g-1)][1-(V₁/V₂)^g-1].

Работа, совершаемая газом при адиабатическом расширении 1®2 определяется площадью светло-закрашенной фигуры на рис.7. Эта работа меньше работы при изотермическом процессе: при адиабатическом расширении происходит охлаждение газа, тогда как при изотермическом процессе температура поддерживается постоянной за счет притока извне эквивалентного количества теплоты. Работа при адиабатическом расширении происходит за счет уменьшения внутренней энергии системы, что и приводит к уменьшению температуры.

Работа, совершаемая при адиабатическом сжатии 1®3, определяется площадью темно-закрашенной фигуры на рис.7 - она совершается внешними силами над газом и приводит к возрастанию его внутренней энергии (к увеличению температуры).

Если газ адиабатически расширяется в вакуум, то он не совершает работу и для такого процесса из первого начала термодинамики Q = DU + A получим U₁ = U₂. Иными словами, при адиабатическом расширении без совершения работы внутренняя энергия газа не изменяется, т.е. не изменяется его температура.

3.5.5. Политропные процессы- это процессы, проходящие при условии постоянства теплоемкости С . Исходя из первого начала термодинамики при условии С = const, можно вывести уравнение политропы pVⁿ = const,

где n = (C-C_p)/(C-C_V) - показатель политропы: С=0, n=g - уравнение адиабаты; С=¥, n=1 - уравнение изотермы; C=C_p, n=0 - уравнение изобары,; С=С_V, n=±¥ - уравнение изохоры. Таким образом, изотермические, изобарические, изохорические и адиабатические процессы являются политропными процессами.