Правила сложения моментов импульса

Лекции 7,8

Принцип Паули

Состояние электрона при его движении в центрально-симметричном поле определяется четырьмя квантовыми числами, как показано в таблице.

Квантовое число	Обо­значе­ние	Квантуемая величина	Принимаемые значения
Главное		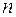Энергия	1,2,3,…
Орбитальное		Механический орбитальный момент	0,1,…,
Магнитное		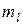Ориентация орбитального момента
Спиновое		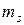Ориентация спинового мо­мента

В нормальном состоянии атома электроны должны располагаться на самых низких доступных для них энергетических уровнях. Казалось бы, в нормальном состоянии все электроны должны находится в состоянии 1s ( ). Однако это не так, поскольку существует принцип Паули: в одном и том же атоме (квантовой системе) не может быть двухэлектронов, обладающих одной и той же совокупностью квантовых чисел.

Исследуем математическую сущность принципа Паули. Возьмем систему, состоящую из двух электронов, находящихся в некотором силовом поле. Координаты первого электрона отметим индексом 1, а координаты второго – индексом 2. Пусть первый электрон находится в квантовом состоянии I, которое описывается волновой функцией , а второй электрон – в квантовом состоянии II с волновой функцией . Поскольку по предположению в состоянии I находится первый электрон, есть амплитуда вероятности найти этот электрон в окрестности точки ; в этом случае является функцией координат первого электрона. Аналогичным образом, функция - амплитуда вероятности найти второй электрон в окрестности точки - является функцией координат второго электрона.

Рассмотрим теперь распределение обоих электронов. Оно описывается функцией, зависящей от координат как первого, так и второго электронов, т.е. от шести координат . «Выключим» для простоты силы, действующие между электронами. Если бы электроны не подчинялись принципу Паули, их движение в отсутствие взаимодействия было бы независимым. В теории вероятностей показывается, что вероятность события, представляющего собой совпадение двух независимых событий, равна произведению вероятностей обоих событий. В нашем случае в качестве таких событий следует рассматривать нахождение первого электрона в окрестности точки 1 и второго в окрестности точки 2. Поэтому следовало бы ожидать, что амплитуда вероятности, описывающая поведение электронов имеет вид:

(2.26)

Легко видеть, что такая запись находится в противоречии с представлениями квантовой механики. В самом деле, написанная формула утверждает, что функция описывает распределение именно первого электрона, в то время как поведение второго электрона описывается функцией . Иначе говоря, наша запись содержит в неявном виде предположение о том, что можно установить, какой из электронов является первым, а какой – вторым.

Предположение о том, что электроны и любые другие физические объекты при желании можно отличить друг от друга, всегда делается в классической физике, и на первый взгляд, очевидно. В микромире, однако, многие привычные понятия приходится пересматривать. Мы уже хорошо знаем, что все электроны вполне тождественны, так что отличить их друг от друга невозможно. Представляется, что отличить электроны можно по их начальному состоянию, скажем, назвать первым электрон, который в некоторый момент времени находился в окрестности точки 1, а вторым – тот, который в это время был около точки 2. Сможем ли мы в дальнейшем установить, который из электронов является первым, а какой вторым? Легко видеть, что нет. В самом деле, положение каждого из электронов описывается - функциями, "размазанными", вообще говоря, по всему пространству. А так как электроны не имеют траекторий, то невозможно установить, какой из электронов пришел в ту точку, где он через какое-то время был обнаружен. Таким образом, выражение (2.26) позволяет знать об электронах больше, чем может быть обнаружено на опыте, и уже поэтому не может быть правильным.

Существует два способа записи амплитуды вероятности, которые не обладают отмеченным недостатком:

(2.27)

(2.28)

В выражениях (2.27) и (2.28) и обозначают совокупность трех координат и , соответственно. Каждое из этих выражений состоит из двух членов. Первый член описывает состояние, когда в состоянии I находится первый электрон, а в состоянии II – второй электрон. Второй член – состояние, когда в состоянии I находится второй электрон, а в состоянии II – первый. Поскольку эти состояния теперь смешаны, узнать, где находится какой электрон, невозможно.

Выражения (2.27), (2.28) не являются точными, так как не удовлетворяют условию нормировки. Точные выражения отличаются от них, как показывает квантовая механика, множителем .

Обратим внимание на важную особенность функций и определенными формулами (2.27) и (2.28). Назовем первый электрон вторым, а второй первым. От такого переименования электронов, конечно, ничего измениться не должно. Легко видеть, однако, что при переименовании электронов функция совсем не изменяется, а функция меняет знак. Поскольку распределение частиц зависит от квадрата модуля пси-функции, изменение знака функции ни на каких наблюдаемых на опыте явлениях обнаружено быть не может. Характер симметричной функции и антисимметричной функции , однако, существенно различен. Рассмотрим, например, случай когда оба состояния и идентичны. Функция при этом тождественно обратится в нуль, в то время как с функции ничего существенного не произойдет. Частицы, которые описываются антисимметричными функциями, не могут поэтому быть в одинаковом состоянии, в то время как частицы, которые описываются симметричными функциями, в одинаковых состояниях быть могут.

Опыт показывает: электроны и все другие частицы, обладающие полуцелым спином (протоны, нейтроны и т.д.), описываются антисимметричными функциями. Мы показали, что частицы, описываемые антисимметричными волновыми функциями, не могут находится в одном и том же состоянии. Существование принципа Паули для электронов является, таким образом, необходимым (но не единственным!) следствием более общего утверждения о том, что электроны должны описываться антисимметричными волновыми функциями.

Опыт показывает также, что все частицы, обладающие целым спином (световые кванты, пи-мезоны и т.д.), описываются симметричными волновыми функциями. Такие частицы принципу Паули не подчиняются.

Частицы с полуцелым спином, на которые распространяется принцип Паули, называются частицами Ферми-Дирака, или фермионами. Частицы с целым спином называются частицами Бозе-Эйнштейна, или бозонами. Распределение микрообъектов на ферми-частицы и бозе-частицы справедливо не только для элементарных частиц, но также и для сложных образований, например, для атомных ядер или самих атомов. Правило остается тем же: симметричными волновыми функциями описываются сложные частицы с целым спином, т.е. системы, состоящие из бозонов или четного числа фермионов. Если же число фермионов нечетное, то система описывается антисимметричной волновой функцией и подчиняется принципу Паули. Альфа-частицы (ядра атома гелия ), например, состоящие из четырех фермионов (двух протонов и двух нейтронов) являются бозонами, и принцип Паули на них не распространяется.

На первый взгляд кажется, что необходимость симметризации (или антисимметризации) волновых функций должна приводить к невероятным трудностям. В самом деле, при решении любой задачи об электронах мы должны, строго говоря, найти волновые функции всех электронов во Вселенной, и из них составить полностью антисимметричную функцию, т.е. функцию, меняющую знак при перестановке любой пары электронов. Задача действительно фантастическая. К счастью, учет всех электронов вовсе не является необходимым. Простое математическое исследование показывает, что нет необходимости принимать во внимание электроны, волновые функции которых не перекрываются (или почти не перекрываются) с волновой функцией рассматриваемого электрона. Практическое правило заключается в том, что волновая функция должна быть антисимметричной для всех электронов с заметно перекрывающимися -функциями. Поэтому вычисления, произведенные нами для атома водорода применимы для изолированных атомов водорода и не годятся для молекул. В конденсированных веществах только «внутренние электроны» могут рассматриваться как принадлежащие одному атому.

Правила сложения моментов импульса

Рассмотрим систему, состоящую из двух частиц, имеющих орбитальные моменты и , и найдем возможные значения суммарного момента этой системы. Поскольку и векторные величины, то и складываться они должны по правилам сложения векторов. Абсолютное значение суммарного момента зависит от взаимной ориентации составляющих моментов и . В квантовой механике векторный характер моментов сохраняется, однако следует помнить, что как сам момент , так и его проекция квантуются по известным правилам:

, (2.29)

где орбитальное квантовое число системы, а магнитное квантовое число, определяющее проекцию момента на ось . Квантовый характер моментов лишает момент импульса простой классической наглядности и заставляет внимательно исследовать правила их сложения.

Найдем связь между квантовыми числами и квантовыми числами . Рассмотрим для этого проекции моментов импульса на ось , рис.47. Обычные правила сложения векторов показывают, что:

(2.30)

Обратимся теперь к возможным значениям . Нам известно, что должно быть целым числом, величина которого зависит от взаимной ориентации и . Задача будет полностью решена, если будут найдены максимальное и минимальное значения квантового числа . Наибольшее возможное значение равно наибольшему возможному числу . Следовательно:

(2.31)

Рассмотрим геометрический смысл найденного решения. Выберем наибольший из векторов и . Направим ось так, чтобы проекция на эту ось была максимальной, то есть , рис.48. (Направление оси и вектора , как легко видеть, при этом не совпадают, а образуют наименьший возможный угол). Направим, далее, вектор так, чтобы его проекция на ту же ось была максимальной и, следовательно, равнялась . В классической физике этот случай соответствует сложению параллельных векторов.

Минимальное значение суммарного вектора в классической физике получается при антипараллельной ориентации векторов. На векторной диаграмме моментов минимальное значение получается при такой ориентации векторов и , когда проекции этих векторов на ось максимальны, но имеют различные знаки. Оставим направление прежним, а направление заменим на противоположное, рис.49; проекция это вектора на ось теперь равна . Поэтому имеем:

Это выражение правильно лишь при . При оно становится отрицательным, что не имеет смысла. Правильная запись имеет вид:

(2.32)

Согласно (2.31) и (2.32) имеем:

(2.33)

Из (2.33) следует, что может принимать значение, если , и значение если .

Случай (2.31) в классической физике соответствует сложению параллельных векторов, а (2.32) - сложению антипараллельных векторов. В квантовой механике, как мы видим, дело обстоит сложнее. В самом деле, ни один момент не может быть направлен по одной какой-либо оси, так как направления моментов несколько "размазаны" из-за неопределенности проекций на оси и при определенной проекции на ось . Из-за этой "размазанности" квадрат момента равен , а не , так что . По той же причине:

Покажем, что выражение (2.33) определяет все возможные значения . Число возможных состояний для частицы с моментом определяется числом , и равно . Аналогично, число возможных состояний для второй частицы равно , а число возможных состояний для системы двух независимых части равно, очевидно, .

Рассмотрим теперь ту же задачу, исходя из результирующего механического момента системы .

Число возможных состояний с различными для каждого равно, как всегда, , а число различных значений определяется неравенством (2.33). Пусть для определенности ; полное число состояний с различными возможными значениями и равно сумме:

(2.34)

Члены суммы образуют арифметическую прогрессию с разностью, равной 2. Сумма (2.34) может быть найдена как сумма арифметической прогрессии, состоящей из членов:

При результат расчета, безусловно, оказывается тем же самым.

Итак, правило (2.33) действительно позволяет находить все возможные значения суммарного механического момента двух частиц. (По этому же правилу находится суммарный механический момент частицы, если она участвует одновременно в двух вращениях.)

Если система состоит не из двух, а из многих частиц, то квантовое число , определяющее результирующий момент находится путем последовательного применения правила (2.33).

Например: . Возможны значения суммарного момента первой и второй частиц: т.е. L = 0,1,2 Сложение первого из этих результатов с дает и далее , т.е., L = 3, 2, 1. Следовательно, квантовое число, определяющее результирующий момент в рассматриваемом случае может иметь значения:

L = 0,1,2,3; L _min = 0; L _max = 3