Молекулярно-кинетическая теория
Краткая теория
 Относительная молекулярная (атомная) масса – отношение массы молекулы (атома)
Относительная молекулярная (атомная) масса – отношение массы молекулы (атома)  данного вещества к
данного вещества к  массы атома углерода
массы атома углерода  (изотопа 12С):
(изотопа 12С):
 .
.
 Моль– количество вещества, в котором содержится столько же молекул или атомов, сколько атомов содержится в 0.012 кг углерода 12С.
Моль– количество вещества, в котором содержится столько же молекул или атомов, сколько атомов содержится в 0.012 кг углерода 12С.
 В одном моле любого вещества содержится одно и то же число молекул или атомов,которое называется числом (постоянной) Авогадро. Число Авогадро равно
В одном моле любого вещества содержится одно и то же число молекул или атомов,которое называется числом (постоянной) Авогадро. Число Авогадро равно

 Количество веществаν – число молей, равное отношению числа молекул N к числу Авогадро:
Количество веществаν – число молей, равное отношению числа молекул N к числу Авогадро:
 .
.
 Молярная массаµ – масса одного моля вещества:
Молярная массаµ – масса одного моля вещества:
 ,
,
где  – масса одной молекулы;
– масса одной молекулы;  – число Авогадро. Поскольку масса вещества – это произведение массы одной молекулы на их количество:
– число Авогадро. Поскольку масса вещества – это произведение массы одной молекулы на их количество:  , то количество вещества равно:
, то количество вещества равно:
 .
.
 Относительная молекулярная масса вещества:
Относительная молекулярная масса вещества:
 ,
,
где ni – число атомов i-го химического элемента, входящего в состав молекулы данного вещества;  – относительная атомная масса этого элемента. Относительные атомные массы приводятся в таблице Д. И. Менделеева.
– относительная атомная масса этого элемента. Относительные атомные массы приводятся в таблице Д. И. Менделеева.
 Связь молярной массы с относительной молекулярной массой:
Связь молярной массы с относительной молекулярной массой:
 .
.
 Давление, производимое газом на стенки сосуда:
Давление, производимое газом на стенки сосуда:
 ,
,
где n – концентрация молекул;  – масса одной молекулы;
– масса одной молекулы;  – средняя квадратичная скорость молекул.
– средняя квадратичная скорость молекул.
 Концентрация молекул – число молекул в единице объёма:
Концентрация молекул – число молекул в единице объёма:
 .
.
 Средняя квадратичная скорость (по определению):
Средняя квадратичная скорость (по определению):
 ,
,
где N – число молекул; суммирование происходит по всем молекулам. Или:
 ,
,
где  – масса молекулы;
– масса молекулы;  – постоянная Больцмана; Т – термодинамическая температура µ – молярная масса газа;
– постоянная Больцмана; Т – термодинамическая температура µ – молярная масса газа;  – универсальная газовая постоянная.
– универсальная газовая постоянная.
 Универсальная газовая постоянная равна
Универсальная газовая постоянная равна
 ,
,
где k – постоянная Больцмана;  – число Авогадро.
– число Авогадро.
 Уравнение состояния идеального газа (уравнениеМенделеева-Клапейрона:
Уравнение состояния идеального газа (уравнениеМенделеева-Клапейрона:
 , или
, или  ,
,
где m – масса газа; µ – его молярная масса; Т – термодинамическая температура;  – количество вещества; R – универсальная газовая постоянная.
– количество вещества; R – универсальная газовая постоянная.
 Термодинамическая температура (температура по шкале Кельвина):
Термодинамическая температура (температура по шкале Кельвина):
 ,
,
где t – температура в градусах Цельсия.
 Давление газа равно:
Давление газа равно:
 ,
,
где k – постоянная Больцмана; n – концентрация молекул, Т термодинамическая температура.
 Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений входящих в смесь газов:
Закон Дальтона. Давление смеси идеальных газов равно сумме парциальных давлений входящих в смесь газов:
 ,
,
где  – номер компоненты смеси;
– номер компоненты смеси;  – её парциальное давление, то есть то давление, которое производил бы данный сорт газа, если бы только один занимал весь объём, равный полному объёму смеси; K – число компонентов смеси.
– её парциальное давление, то есть то давление, которое производил бы данный сорт газа, если бы только один занимал весь объём, равный полному объёму смеси; K – число компонентов смеси.
 Массовая доля i-го компонента смеси газов
Массовая доля i-го компонента смеси газов
 ,
,
где mi –масса i-го компонента смеси; m – масса смеси.
 Основное уравнение молекулярно-кинетической теории
Основное уравнение молекулярно-кинетической теории
– для давления:
 ;
;
– для температуры:
 ,
,
где  – средняя кинетическая энергия поступательного движения молекул газа.
– средняя кинетическая энергия поступательного движения молекул газа.
 Теорема о равнораспределении энергии по степеням свободы. На любую степень свободы приходится в среднем одинаковая энергия, равная
Теорема о равнораспределении энергии по степеням свободы. На любую степень свободы приходится в среднем одинаковая энергия, равная
 .
.
 Число степеней свободы
Число степеней свободы  равно числу независимых координат, однозначно определяющих положение тела (или молекулы) в пространстве. Для одноатомных молекул
равно числу независимых координат, однозначно определяющих положение тела (или молекулы) в пространстве. Для одноатомных молекул  , для двухатомных
, для двухатомных  , для произвольных жёстких многоатомных –
, для произвольных жёстких многоатомных –  .
.
 Средняя энергия одной молекулы, у которой
Средняя энергия одной молекулы, у которой  степеней свободы, равна
степеней свободы, равна
 .
.
 Внутренняя энергия U идеального газа:
Внутренняя энергия U идеального газа:
 ,
,
где i – число степеней свободы молекул газа.
Примеры решения задач
Пример 4.1.Определить линейные размеры атома железа и его массу. Плотность железа равна 7800 кг/м3, молярная масса равна 0.056 кг/моль.
| Дано: ρ=7800 кг/м3 μ=0.056 кг/моль |
| Найти: d=? m0=? |
Решение
 Число атомов (молекул) в одном моле любого вещества равно числу Авогадро
Число атомов (молекул) в одном моле любого вещества равно числу Авогадро  . Масса одного атома
. Масса одного атома  .
.
Для нахождения диаметра атома будем считать, что атомы в кристаллической решётке упакованы подобно шарикам (рис.4.1), то есть на один атом в среднем приходится объём, приблизительно равный  . Тогда для плотности:
. Тогда для плотности:  . Отсюда
. Отсюда  . Вычисления:
. Вычисления:
 ;
;  .
.
Ответ:  ;
;  .
.
Основы термодинамики
Краткая теория
 Средняя кинетическая энергия поступательного движения одной молекулы идеального одноатомного газа
Средняя кинетическая энергия поступательного движения одной молекулы идеального одноатомного газа
 ,
,
где k – постоянная Больцмана, T – абсолютная температура.
 Внутренняя энергия идеального газа равна:
Внутренняя энергия идеального газа равна:
 , или
, или
 , или
, или
 ,
,
где i – число степеней свободы молекул, равное 3 для одноатомного газа; 5 для двухатомного и 6 для многоатомного с нелинейными молекулами; R – универсальная газовая постоянная, T – абсолютная температура,  – молярная теплоёмкость газа при постоянном объёме;
– молярная теплоёмкость газа при постоянном объёме;  – количество вещества ( число молей), m – масса газа, μ – его молярная масса, p – давление газа, V – его объём.
– количество вещества ( число молей), m – масса газа, μ – его молярная масса, p – давление газа, V – его объём.
 Уравнение состояния идеального газа (уравнениеМенделеева-Клапейрона:
Уравнение состояния идеального газа (уравнениеМенделеева-Клапейрона:
 , или
, или  ,
,
где m – масса газа; µ – его молярная масса; Т – термодинамическая температура;  – количество вещества; R – универсальная газовая постоянная.
– количество вещества; R – универсальная газовая постоянная.
 Уравнение изотермического процесса (
Уравнение изотермического процесса (  ):
):
 , или
, или  .
.
 Уравнение изохорического процесса (
Уравнение изохорического процесса (  ):
):
 , или
, или  .
.
 Уравнение изобарического процесса (
Уравнение изобарического процесса (  ):
):
 , или
, или  .
.
 Элементарная работа газа при увеличении объёма на
Элементарная работа газа при увеличении объёма на  равна:
равна:
 ,
,
где р – давление газа.
 Работа газа при изменении объёма от V1 до V2:
Работа газа при изменении объёма от V1 до V2:
 .
.
При изобарном процессе работа равна  .
.
 Теплоемкость тела – это количество теплоты, необходимое для нагревания этого тела на один градус (кельвин):
Теплоемкость тела – это количество теплоты, необходимое для нагревания этого тела на один градус (кельвин):
 .
.
 Удельная теплоемкость – это количество теплоты, необходимое для нагревания единицы массы вещества на один градус:
Удельная теплоемкость – это количество теплоты, необходимое для нагревания единицы массы вещества на один градус:
 .
.
 Удельная теплоемкость – это количество теплоты, необходимое для нагревания одного моля вещества на один градус:
Удельная теплоемкость – это количество теплоты, необходимое для нагревания одного моля вещества на один градус:
 .
.
 Связь между молярной (С) и удельной (с) теплоемкостями:
Связь между молярной (С) и удельной (с) теплоемкостями:
 ,
,
где μ – молярная масса.
 Молярная теплоёмкость идеального газа при постоянном объёме:
Молярная теплоёмкость идеального газа при постоянном объёме:
 ,
,
где i – число степеней свободы молекул; R – универсальная газовая постоянная. Для одноатомных газов  .
.
 Молярная теплоёмкость идеального газа при постоянном давлении:
Молярная теплоёмкость идеального газа при постоянном давлении:
 ,
,
где i – число степеней свободы молекул; R – универсальная газовая постоянная. Для одноатомных газов  .
.
 Уравнение Майера:
Уравнение Майера:
 .
.
 Количество теплоты, поглощённой в процессах:
Количество теплоты, поглощённой в процессах:
– нагревания  ,
,
– плавления:  ,
,
– парообразования  ,
,
где  – удельная теплоемкость тела,
– удельная теплоемкость тела,  – удельная теплота плавления, r – удельная теплота парообразования, m – масса.
– удельная теплота плавления, r – удельная теплота парообразования, m – масса.
 Количество теплоты, выделившейся в процессе сгорания топлива:
Количество теплоты, выделившейся в процессе сгорания топлива:
 ,
,
где  – удельная теплота сгорания топлива, m – его масса.
– удельная теплота сгорания топлива, m – его масса.
 Первый закон (первое начало) термодинамики: количество теплоты Q, сообщенное системе, идет на увеличение её внутренней энергии
Первый закон (первое начало) термодинамики: количество теплоты Q, сообщенное системе, идет на увеличение её внутренней энергии  и совершение этой системой работы
и совершение этой системой работы  против внешних сил:
против внешних сил:
 .
.
Первое начало термодинамики:
– для изохорного процесса  ;
;
– для изобарного процесса:  ;
;
– для изотермического процесса:  ;
;
– для адиабатного процесса:  .
.
 Коэффициент полезного действия (КПД) тепловой машины:
Коэффициент полезного действия (КПД) тепловой машины:
 ,
,
где  – полезная работа, совершаемая машиной;
– полезная работа, совершаемая машиной;  – количество теплоты, полученное рабочим телом от нагревателя;
– количество теплоты, полученное рабочим телом от нагревателя;  – количество теплоты, отданное рабочим телом холодильнику. Идеальная тепловая машина, работающая по циклу Карно (рис.5.1), при заданных температурах нагревателя
– количество теплоты, отданное рабочим телом холодильнику. Идеальная тепловая машина, работающая по циклу Карно (рис.5.1), при заданных температурах нагревателя  и охладителя
и охладителя  , имеет максимальный КПД, не зависящий от природы рабочего тела:
, имеет максимальный КПД, не зависящий от природы рабочего тела:
 .
.
 |
Примеры решения задач
Дано: 1) P1=const T2=3T1 2) V2=const   |
| Найти: Q1=? |
Пример 5.1.Некоторое количество газа (криптон) нагрели при постоянном давлении. Температура газа при этом повысилась в 3 раза. Затем при изохорном охлаждении газ отдал количество теплоты 9 кДж; температура при этом понизилась в 2 раза. Какое количество теплоты было сообщено газу при изобарном процессе?
Решение
1) P1=const. По первому закону термодинамики для процесса 1-2 (рис.5.2):
 .
.
С учётом условия T2=3T1:  ;
;

 . (1)
. (1)
2) V2=const. При изохорном процессе работа не совершается: А2=0. Тогда из первого закона термодинамики для процесса 2-3:
 ;
;
 . (2)
. (2)
Разделим почленно (1) на (2):
 .
.
Отсюда  .
.
Ответ:  .
.
Электростатика
Краткая теория
· Закон сохранения заряда: в изолированной системе алгебраическая сумма зарядов всех частиц остается неизменной:
 .
.
· Закон Кулона. Сила  взаимодействия двух неподвижных точечных зарядов q1 и q2 прямо пропорциональна величине каждого заряда и обратно пропорциональна квадрату расстояния r между ними:
взаимодействия двух неподвижных точечных зарядов q1 и q2 прямо пропорциональна величине каждого заряда и обратно пропорциональна квадрату расстояния r между ними:
 , или
, или  ,
,
где значение коэффициента k в СИ равно  ;
;  – электрическая постоянная, e – диэлектрическая проницаемость среды.
– электрическая постоянная, e – диэлектрическая проницаемость среды.
· Диэлектрическая проницаемость среды e показывает, во сколько раз взаимодействие зарядов в среде ослабляется по сравнению с вакуумом:
 , или
, или  ,
,
где F – сила взаимодействия зарядов в среде, F0 – в вакууме; E – напряжённость поля в среде, E0 – в вакууме.
· Напряженность электрического поля равна силе, действующей на единичный точечный положительный пробный заряд q, помещенный в данную точку поля:
 .
.
· Сила, действующая на точечный заряд q, помещенный в электрическое поле
 .
.
· Напряженность электрического поля, создаваемого точечным зарядом q на расстоянии r от заряда
 .
.
· Напряженность электрического поля, создаваемого металлической сферой радиусом R, несущей заряд q, на расстоянии r от центра сферы:
а) внутри сферы (r<R) E=0;
б) на поверхности сферы (r=R)  ;
;
в) вне сферы (r>R)  .
.
Здесь e – диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
· Принцип суперпозиции (наложения) электрических полей: напряженность  результирующего электрического поля, создаваемого несколькими источниками в некоторой точке пространства, равна геометрической сумме напряженностей полей
результирующего электрического поля, создаваемого несколькими источниками в некоторой точке пространства, равна геометрической сумме напряженностей полей  , созданных в данной точке каждым источником в отдельности, причем каждая составляющая не зависит от наличия остальных полей:
, созданных в данной точке каждым источником в отдельности, причем каждая составляющая не зависит от наличия остальных полей:

 .
.
В случае двух электрических полей с напряженностями  и
и  модуль результирующего вектора напряженности (рис.6.1):
модуль результирующего вектора напряженности (рис.6.1):
 ,
,
где a – угол между векторами  и
и  (рис.4.1).
(рис.4.1).
· Поверхностная плотность заряда, распределенного по поверхности, есть величина, равная заряду, приходящемуся на единицу площади поверхности:
 .
.
· Линейная плотность заряда, распределенного по нити, есть величина, равная заряду, приходящемуся на единицу её длины:
 .
.
· Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью
 ,
,
где s – поверхностная плотность заряда.
· Напряженность поля, создаваемого двумя параллельными бесконечными равномерно и разноименно заряженными плоскостями, с одинаковой по модулю поверхностной плотностью  заряда (поле плоского конденсатора)
заряда (поле плоского конденсатора)
 .
.
Приведенная формула справедлива для вычисления напряженности поля между пластинами плоского конденсатора (в средней части его) только в том случае, если расстояние между пластинами много меньше линейных размеров пластин конденсатора.
· Потенциал электрического поляв данной точке равен отношению потенциальной энергии, которой обладает положительный точечный заряд, помещенный в данную точку поля, к величине этого заряда:
 .
.
Иначе: потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность, к этому заряду:
 .
.
Потенциал электрического поля в бесконечности условно принят равным нулю.
· Работа сил электрического поля при перемещении точечного заряда q из точки с потенциалом  в точку с потенциалом
в точку с потенциалом  :
:
 .
.
Для однородного поля A=q∙E∙l∙cosa, где l – перемещение; a – угол между направлениями вектора  и перемещения
и перемещения  .
.
· Потенциал поля, созданного уединенным точечным зарядом  на расстоянии
на расстоянии  от заряда, равен
от заряда, равен
 .
.
· Потенциал электрического поля, создаваемого металлической сферой радиусом R, несущей заряд q, на расстоянии r от центра сферы:
внутри сферы (r<R)  ;
;
на поверхности сферы (r=R)  ;
;
вне сферы (r>R)  .
.
Здесь e – диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.
· Принцип суперпозиции: потенциал результирующего поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов полей, созданных в данной точке каждым из зарядов:
 .
.
· Энергия W взаимодействия системы N точечных зарядов q1, q2, ..., qN определяется работой, которую эта система зарядов может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой
 ,
,
где  – потенциал поля, создаваемого всеми (N–1) зарядами (за исключением i-го) в точке, где расположен заряд qi.
– потенциал поля, создаваемого всеми (N–1) зарядами (за исключением i-го) в точке, где расположен заряд qi.
· Связь напряжённости и потенциала. В случае однородного поля, т. е. поля, напряженность которого в каждой точке его одинакова как по модулю, так и по направлению
 ,
,
где j1 и j2 – потенциалы точек двух эквипотенциальных поверхностей; d – расстояние между этими поверхностями вдоль электрической силовой линии.
· Электрическая емкость уединенного проводника
 ,
,
где q – заряд, сообщенный проводнику; φ – потенциал проводника.
· Электрическая ёмкость уединенной проводящей сферы радиусом R,находящейся в бесконечной среде с диэлектрической проницаемостью ε
 .
.
Если сфера полая и заполнена диэлектриком, то электроемкость её от этого не изменяется.
· Емкость конденсатора определяется отношением модуля заряда q на одной обкладке к разности потенциалов U между обкладками:
 .
.
· Электрическая емкость плоского конденсатора
 ,
,
где S – площадь пластин (каждой пластины); d – расстояние между ними; ε – диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.
· Электрическая емкость С последовательно соединенных конденсаторов в общем случае (N – число конденсаторов)
 .
.
В случае двух конденсаторов  .
.
В случае п одинаковых конденсаторов с электроемкостью С1 каждый
 .
.
· Электрическая емкость параллельно соединенных конденсаторов в общем случае
C=C1+C2+...+CN.
В случае N одинаковых конденсаторов с электроемкостью С1 каждый:
C=N∙C1.
· Энергия заряженного проводника выражается через заряд q, потенциал φ и электрическую емкость С проводника следующими соотношениями:
 .
.
· Энергия заряженного конденсатора

где С – электрическая емкость конденсатора, q – его заряд, U – разность потенциалов на его пластинах.
· Объемная плотность энергии – это энергия единицы объема:
 .
.
· Объемная плотность энергии электростатического полянапряжённостью Е равна:
 .
.
Примеры решения задач
Пример 6.1.Три одинаковых положительных заряда Q1=Q2=Q3=1 нКл расположены по вершинам равностороннего треугольника (рис. 6.2). Какой отрицательный заряд Q4 нужно поместить в центре треугольника, чтобы сила притяжения с его стороны уравновесила силы взаимного отталкивания зарядов, находящихся в вершинах?
Решение
| Дано: Q1=Q2=Q3=1 нКл |
| Найти: Q4=? |
 Все три заряда, расположенных по вершинам треугольника, находятся в одинаковых условиях, поэтому для решения задачи достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы один из трех зарядов, например Q1, находился в равновесии.
Все три заряда, расположенных по вершинам треугольника, находятся в одинаковых условиях, поэтому для решения задачи достаточно выяснить, какой заряд следует поместить в центре треугольника, чтобы один из трех зарядов, например Q1, находился в равновесии.
В соответствии с принципом суперпозиции на заряд действует каждый заряд независимо от остальных. Поэтому заряд Q1 будет находиться в равновесии, если векторная сумма действующих на него сил равна нулю:
 , (1)
, (1)
где  – силы, с которыми действуют на заряд Q1 заряды Q2, Q3 и Q4 соответственно;
– силы, с которыми действуют на заряд Q1 заряды Q2, Q3 и Q4 соответственно; 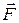 – равнодействующая сил
– равнодействующая сил  и
и  .
.
Так как силы 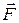 и
и  направлены по одной прямой, то из векторного равенства (1) следует равенство величин:
направлены по одной прямой, то из векторного равенства (1) следует равенство величин:
F4=F. (2)
По теореме косинусов с учётом, что F3=F2, получим
 ,
,
где α=1200, так как треугольник – равносторонний. Тогда
 (3)
(3)
Применяя закон Кулона и имея в виду, что Q2=Q3=Q1, найдем
 ;
;  (4)
(4)
Из (2), (3) и (4) получим
 ,
,
 . (5)
. (5)
Из геометрических построений в равностороннем треугольнике следует, что
 .
.
С учетом этого формула (5) примет вид:
 .
.
Подставив сюда значение Q1, получим Q4=0,58нКл.
Ответ: Q4=0,58нКл. Равновесие системы зарядов будет неустойчивым.
Пример 6.2.Найти работу А поля по перемещению заряда Q=10 нКл из точки 1 в точку 2 (рис. 6.3). Точки находятся между двумя разноименно заряженными бесконечными параллельными плоскостями, расстояние l между которыми равно 3 см. Поверхностная плотность заряда плоскостей s=0,4 мкКл/м2.
| Дано: Q=10 нКл s=0,4 мкКл/м2 l=3 см |
| Найти: А=? |
Решение
Возможны два способа решения задачи.
1-й способ. Работу сил поля по перемещению заряда Q из точки 1 поля с потенциалом j1 в точку 2поля с потенциалом j2 найдем по формуле
A=Q(j1–j2). (1)
Для определения потенциалов в точках 1 и 2 проведем через эти точки эквипотенциальные поверхности I и II. Эти поверхности будут плоскостями, так как поле между двумя равномерно заряженными бесконечными параллельными плоскостями однородно. Для такого поля справедливо соотношение
j1–j2=E∙l, (2)
где Е – напряженность поля; l – расстояние между эквипотенциальными поверхностями.
 Напряженность поля между параллельными бесконечными разноименно заряженными плоскостями E=s/e0. Подставив это выражение Е в формулу (2) с учётом (1), получим
Напряженность поля между параллельными бесконечными разноименно заряженными плоскостями E=s/e0. Подставив это выражение Е в формулу (2) с учётом (1), получим
 .
.
2-й способ. Так как поле однородно, то сила, действующая на заряд Q при его перемещении постоянна. Поэтому работу перемещения заряда из точки 1 в точку 2 можно подсчитать по формуле
A=F∙Dr∙cosa, (3)
где F – сила, действующая на заряд; Dr – модуль перемещения заряда Q из точки 1 в точку 2;a – угол между направлениями перемещения и силы. Сила равна
 . (4)
. (4)
Заметив, что Dr∙cosa=l, из (3) и (4) получим
 . (5)
. (5)
Оба решения приводят к одному и тому же результату. Подстановка:
 .
.
Ответ: A=13,6мкДж.
Пример 6.3.Электрон со скоростью υ=1,83×106 м/с влетел в однородное электрическое поле в направлении, противоположном вектору напряженности поля. Какую разность потенциалов U должен пройти электрон, чтобы иметь энергию Ei=13,6 эВ? (Обладая такой энергией, электрон при столкновении с атомом водорода может ионизировать его.)
| Дано: υ=1,83×106 м/с Ei=13,6 эВ |
| Найти: U=? |
Решение
Электрон должен пройти такую разность потенциалов U, чтобы приобретенная при этом энергия W в сумме с кинетической энергией  , которой обладал электрон перед вхождением в поле, составила энергию, равную энергии ионизации Ei, т. е. W+
, которой обладал электрон перед вхождением в поле, составила энергию, равную энергии ионизации Ei, т. е. W+  =Ei. Выразив в этой формуле W=e∙U и
=Ei. Выразив в этой формуле W=e∙U и  , получим e∙U+
, получим e∙U+  =Ei. Отсюда
=Ei. Отсюда
 .
.
Электрон-вольт (эВ) – энергия, которую приобретает частица, имеющая заряд, равный заряду электрона, прошедшая разность потенциалов 1 В:
1 эВ=1,6·10-19 Дж.
Вычисления (здесь m=9.1.10-31 кг – масса электрона; е=1.6.10-19 – элементарный заряд, то есть модуль заряда электрона):
 В.
В.
Ответ: U=4.15 В.
Пример 6.4. Два плоских конденсатора одинаковой электроемкости С1=С2=С соединены в батарею последовательно и подключены источнику тока с электродвижущей силой ε. Как изменится разность потенциалов U1 на пластинах первого конденсатора, если пространство между пластинами второго конденсатора, не отключая источника тока, заполнить диэлектриком с диэлектрической проницаемостью 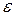 =7?
=7?
Дано: С1=С2=С 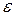 =7 =7 |
Найти:  |
Решение
До заполнения второго конденсатора диэлектриком разность потенциалов на пластинах обоих конденсаторов была одинакова: U1=U2=ε/2. После заполнения электроемкость второго конденсатора возросла в ε раз:
 .
.
Электроемкость С первого не изменилась, т. е.  .
.
Так как источник тока не отключался, то общая разность потенциалов на батарее конденсаторов осталась прежней, она лишь перераспределилась между конденсаторами. На первом конденсаторе
