Среднее число столкновений и средняя длина свободного пробега
Конечные размеры молекул их огромная концентрация в газах при обычных условиях приводят к тому, что молекулы непрерывно сталкиваются друг с другом. Между двумя последовательными столкновениями молекулы движутся равномерно и прямолинейно.
Расстояние λ, которое проходит молекула за время свободного пробега от одного столкновения до следующего называется длиной свободного пробега.
Эти расстояния различны, так как в молекулярной физике имеем дело с огромным числом молекул и они находятся в беспорядочном движении, то можно говорить о средней длине свободного пробега молекул <λ>.
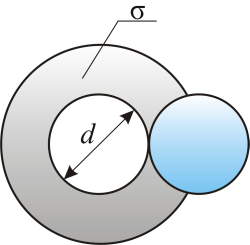
Для вычисления длины свободного пробега примем определенную модель молекул газа. Будем считать, что молекулы представляют собой шарики диаметром d порядка 10-10 м, зависящие от химической природы газа. Минимальное расстояние, на которое сближаются при столкновении центры двух молекул, называется эффективным диаметром молекулы d(рис.1).
Рассчитаем среднее число столкновений <z>, которое испытывает молекула за единицу времени при своем движении в однородном газе.
Так за 1 с молекула проходит путь, равный средней арифметической скорости <υарф>, и если <z> – среднее число столкновений, испытываемых одной молекулой газа за 1 с, то средняя длина свободного пробега:
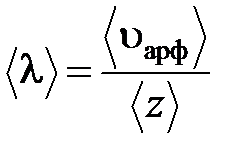
Для определения <z> представим себе молекулу в виде шарика диаметром d, которая движется среди других «застывших» молекул, со скоростью равной средней арифметической скорости <υарф>.
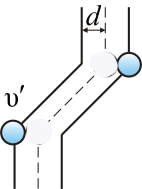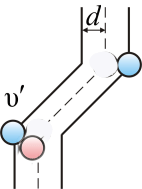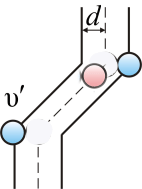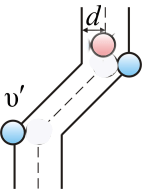
При своем движении молекула будет сталкиваться со всеми молекулами газа, центры которых отстоят от траектории движения ее центра на расстояниях меньших или равных диаметру молекулы d, т.е. лежат внутри «ломанного» цилиндра радиусом d (рис.2). За единицу времени рассматриваемая молекула столкнется со всеми частицами, центры которых лежат внутри этого цилиндра.
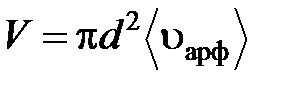
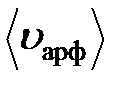
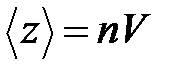 Среднее число столкновений за 1 с равно числу молекул в объеме «ломанного» цилиндра:
Среднее число столкновений за 1 с равно числу молекул в объеме «ломанного» цилиндра:
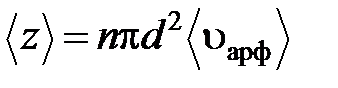 где n – концентрация молекул, ( - средняя скорость молекул газа или путь, пройденный ею за 1 с). Таким образом, среднее число столкновений:
где n – концентрация молекул, ( - средняя скорость молекул газа или путь, пройденный ею за 1 с). Таким образом, среднее число столкновений:
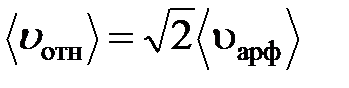
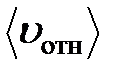
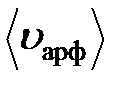 В начале было сделано неверное предположение о том, что все молекулы, кроме одной неподвижны. В действительности все молекулы движутся и возможность их соударения зависит от их относительной скорости. Поэтому в формулу вместо средней арифметической скорости должна входить средняя относительная скорость , которая равна:
В начале было сделано неверное предположение о том, что все молекулы, кроме одной неподвижны. В действительности все молекулы движутся и возможность их соударения зависит от их относительной скорости. Поэтому в формулу вместо средней арифметической скорости должна входить средняя относительная скорость , которая равна:
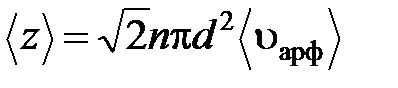
Поэтому среднее число соударений должно определяться по формуле:
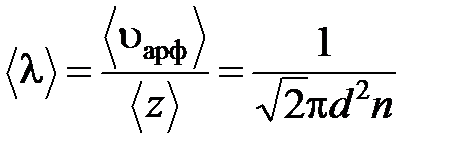 Средняя длина свободного пробега:
Средняя длина свободного пробега:
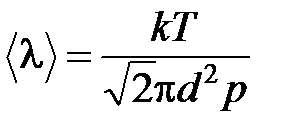
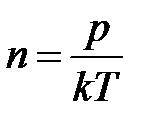
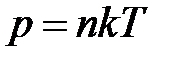 Из уравнения состояния идеального газа:
Из уравнения состояния идеального газа:
следует: , тогда
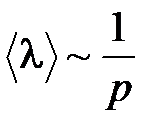 Получаем, что при постоянной температуре концентрация молекул пропорциональна давлению газа, то средняя длина свободного пробега обратно пропорциональна давлению:
Получаем, что при постоянной температуре концентрация молекул пропорциональна давлению газа, то средняя длина свободного пробега обратно пропорциональна давлению:
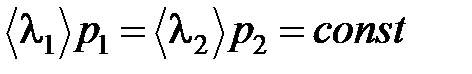 Для данного газа при постоянной температуре (Т=const) и различных давлениях р1 и р2 имеем:
Для данного газа при постоянной температуре (Т=const) и различных давлениях р1 и р2 имеем:
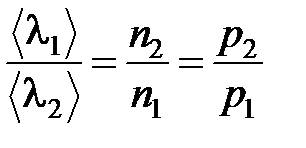 С другой стороны имеем:
С другой стороны имеем:
