Закон Столетова: при фиксированной частоте падающего света число фотоэлектронов, вырываемых из катода за единицу времени, пропорционально интенсивности света
2. Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой ν.
3. Для каждого вещества существует «красная граница» фотоэффекта, т.е. минимальная частота ν0 света (зависит от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен.
Второй и третий законы фотоэффекта не удается объяснить на основе волновых представлений. В самом деле, согласно волновой теории, вырывание электронов из металла должно происходить благодаря их «раскачиванию» в электрическом поле световой волны. Тогда неясно, почему максимальная начальная скорость (максимальная начальная кинетическая энергия) вылетающих электронов зависит от частоты света, а не от амплитуды колебаний вектора  световой волны и связанной с амплитудой интенсивностью волны. Наличие «красной границы» фотоэффекта также несовместимо с волновой теорией, так как свет любой частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла. Кроме того, волновая теория не смогла объяснить безынерционность фотоэффекта, установленую опытами.
световой волны и связанной с амплитудой интенсивностью волны. Наличие «красной границы» фотоэффекта также несовместимо с волновой теорией, так как свет любой частоты, но достаточно большой интенсивности должен был бы вырывать электроны из металла. Кроме того, волновая теория не смогла объяснить безынерционность фотоэффекта, установленую опытами.
Объяснение фотоэффекта было дано на основе квантовой теории. Эйнштейн пошел значительно дальше Планка, предполагавшего, что излучение осуществляется порциями – квантами. Корпускулярные свойства Эйнштейн приписал самому излучению, и отдача энергии  при излучении объясняется тем простым фактом, что никаких других порций излучения (частоты ν) существовать в природе не может.
при излучении объясняется тем простым фактом, что никаких других порций излучения (частоты ν) существовать в природе не может.
Монохроматическое излучение частоты ν состоит всегда из целого числа фотонов (квантов), энергия каждого из которых равна  . При поглощении излучения частоты ν веществом каждый из электронов может поглотить один фотон, приобретая при этом энергию
. При поглощении излучения частоты ν веществом каждый из электронов может поглотить один фотон, приобретая при этом энергию  (и никакую другую).
(и никакую другую).
Если эта энергия достаточна, чтобы электрон мог совершить работу выхода, будет наблюдаться фотоэффект. Если этой энергии недостаточно, фотоэффект наблюдаться не будет: электрон гораздо раньше потеряет приобретенную им энергию (сталкиваясь с ионами и другими электронами и обмениваясь при этом с ними энергией).
Эйнштейн предложил для описания фотоэффекта использовать уравнение:
 ,
,
то есть энергия падающего фотона расходуется на совершение электроном работы выхода А из металла и на сообщение вылетающему фотоэлектрону максимальной кинетической энергии  .
.
Уравнение:
 (1.15)
(1.15)
получило название уравнение Эйнштейна для внешнего фотоэффекта.
Уравнение (1.15) может быть записано в виде:

 то есть
то есть  действительно определяется только частотой света и не зависит от его интенсивности (числа фотонов), так как ни А, ни ν от интенсивности света не зависят. Из этого уравнения получается значение минимальной для данного вещества частоты ν0 («красной границы»), при которой фотоэффект становится возможным, рис.6:
действительно определяется только частотой света и не зависит от его интенсивности (числа фотонов), так как ни А, ни ν от интенсивности света не зависят. Из этого уравнения получается значение минимальной для данного вещества частоты ν0 («красной границы»), при которой фотоэффект становится возможным, рис.6:

«Красная граница» зависит лишь от работы выхода электрона, т.е. от химической природы вещества и состояния его поверхности.
Объяснение безынерциальности фотоэффекта на основе квантовых представлений тривиально: испускание фотоэлектрона происходит сразу, как только на фото катод падает излучение с  .
.
Описанный выше фотоэффект является внешним. При этом падающий на поверхность металла свет испытывает поглощение свободными электронами в очень тонком слое вещества. Поглотив фотоны, электроны приобретают энергию, достаточную для преодоления работы выхода, и часть из них вырывается наружу в вакуум или газ.
В прозрачном диэлектрике или полупроводнике фотон поглощается внутри кристалла электроном, связанным с определенным атомом решетки. При таком внутреннем фотоэффекте электрон вырывается из атома, но остается внутри кристалла. Возникающие узлы с нарушенными электрическими свойствами становятся способными поглощать и рассеивать длинноволновое излучение и тем самым приводят к изменению окраски кристалла. При прохождении жестких  - лучей энергия, поглощенная кристаллом и затрачиваемая на возбуждение его атомов, в некоторых телах способна сразу же излучаться обратно в виде кратковременной вспышки света – сцинтилляции. В случае полупроводников вырванный электрон попадает в зону проводимости, становится свободным и снижает тем самым электрическое сопротивление.
- лучей энергия, поглощенная кристаллом и затрачиваемая на возбуждение его атомов, в некоторых телах способна сразу же излучаться обратно в виде кратковременной вспышки света – сцинтилляции. В случае полупроводников вырванный электрон попадает в зону проводимости, становится свободным и снижает тем самым электрическое сопротивление.
 Вентильный фотоэффект. На границе металл-полупроводник или в области
Вентильный фотоэффект. На границе металл-полупроводник или в области  переходов образуется запорный слой, рис.7. При освещении полупроводника светом с фотонами, обладающими необходимой энергией
переходов образуется запорный слой, рис.7. При освещении полупроводника светом с фотонами, обладающими необходимой энергией  , вырванные из атомов n-полупроводника электроны проходят запорный слой в пропускном направлении и, скапливаясь на внешней границе р-полупроводника, создают постоянную разность потенциалов U. Если соединить проводником обе граничные поверхности, то через него потечет ток, измеряемый гальванометром G. Разность потенциалов U является электродвижущей силой по отношению к замкнутой цепи. Эта электродвижущая сила создает в проводнике фотоэлектрический ток Iф, который пропорционален падающему лучистому потоку Ф.
, вырванные из атомов n-полупроводника электроны проходят запорный слой в пропускном направлении и, скапливаясь на внешней границе р-полупроводника, создают постоянную разность потенциалов U. Если соединить проводником обе граничные поверхности, то через него потечет ток, измеряемый гальванометром G. Разность потенциалов U является электродвижущей силой по отношению к замкнутой цепи. Эта электродвижущая сила создает в проводнике фотоэлектрический ток Iф, который пропорционален падающему лучистому потоку Ф.
Приборы, в которых фотоэффект используется для превращения энергии излучения в электрическую энергию, называются фотоэлементами. Фотоэлементы бывают различных типов. Эти фотоэлементы могут быть основаны как на внешнем фотоэффекте (вакуумные фотоэлементы, газонаполненные фотоэлементы), так и на внутреннем фотоэффекте (фотоэлементы с запирающим слоем).
 Особенно большое усиление тока дает прибор, изобретенный А.А.Кубецким, получивший название фотоэлектронного умножителя (ФЭУ). В этом приборе происходит усиление тока за счет вторичной эмиссии, что приводит к его многократному усилению. Схема прибора приведена на рис.8. Фотоэлектроны с фотокатода ФК ускоряются в электрическом поле и, попадая на первый эмиттер Э1, выбивают из него в
Особенно большое усиление тока дает прибор, изобретенный А.А.Кубецким, получивший название фотоэлектронного умножителя (ФЭУ). В этом приборе происходит усиление тока за счет вторичной эмиссии, что приводит к его многократному усилению. Схема прибора приведена на рис.8. Фотоэлектроны с фотокатода ФК ускоряются в электрическом поле и, попадая на первый эмиттер Э1, выбивают из него в 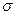 - раз большее число электронов (
- раз большее число электронов (  - коэффициент вторичной эмиссии). Эти электроны, ускоряясь, в свою очередь, попадают на эмиттер Э2, выбивая из него еще большее число электронов. Для того чтобы электроны следовали по необходимым маршрутам, электродам придают специальную форму и сообщают им нужные потенциалы.
- коэффициент вторичной эмиссии). Эти электроны, ускоряясь, в свою очередь, попадают на эмиттер Э2, выбивая из него еще большее число электронов. Для того чтобы электроны следовали по необходимым маршрутам, электродам придают специальную форму и сообщают им нужные потенциалы.
В современных промышленных образцах фотоэлектронного умножителя при девяти ступенях усиления достигается общее увеличение тока в 2.106 раз при напряжении питания в 1000-1500 В.
Давление света
Рассмотрим механическое действие света – давление, оказываемое им на встречные тела. Максвелл, исходя из разработанной им теории электромагнетизма, впервые показал необходимость существования светового давления.
 Качественно механизм давления можно пояснить следующим образом. Пусть на плоскую поверхность Р тела, рис.9, падает нормально электромагнитная волна. Пусть вектора
Качественно механизм давления можно пояснить следующим образом. Пусть на плоскую поверхность Р тела, рис.9, падает нормально электромагнитная волна. Пусть вектора  и
и  лежат в плоскости поверхности
лежат в плоскости поверхности  . Рассмотрим, как они будут воздействовать на электрические заряды, составляющие тело. Под действием силы, действующей со стороны электрической напряженности электромагнитной волны
. Рассмотрим, как они будут воздействовать на электрические заряды, составляющие тело. Под действием силы, действующей со стороны электрической напряженности электромагнитной волны  положительный заряд начнет смещаться вдоль поверхности по направлению
положительный заряд начнет смещаться вдоль поверхности по направлению  , а отрицательный – против
, а отрицательный – против  . Такое смещение зарядов представляет собой поверхностный ток
. Такое смещение зарядов представляет собой поверхностный ток  , параллельный
, параллельный  . В телах со свободными зарядами (проводники) это будет ток проводимости, а в диэлектриках – поляризационный ток смещения. Магнитные силы
. В телах со свободными зарядами (проводники) это будет ток проводимости, а в диэлектриках – поляризационный ток смещения. Магнитные силы  , действующие на ток
, действующие на ток  , будут по закону Ампера направлены перпендикулярно к
, будут по закону Ампера направлены перпендикулярно к  и
и  , то есть внутрь тела. Независимо от их знака, заряды, расположенные на поверхности и связанные с его атомами, «вдавливаются» в тело. Ускорение и скорость
, то есть внутрь тела. Независимо от их знака, заряды, расположенные на поверхности и связанные с его атомами, «вдавливаются» в тело. Ускорение и скорость  пропорциональны величине
пропорциональны величине  . Магнитные же силы пропорциональны
. Магнитные же силы пропорциональны  , а оно в свою очередь, пропорционально плотности электромагнитной энергии падающей волны
, а оно в свою очередь, пропорционально плотности электромагнитной энергии падающей волны  . Точный расчет величины давления света Р по теории Максвелла приводит к выражению:
. Точный расчет величины давления света Р по теории Максвелла приводит к выражению:
 , (1.16)
, (1.16)
где  - коэффициент отражения от данной поверхности.
- коэффициент отражения от данной поверхности.
Для развития электромагнитной теории света было чрезвычайно важно получить прямое экспериментальное подтверждение этого эффекта. Однако обнаружение его осложнялось целым рядом побочных явлений. Частичное поглощение падающего света приводит к нагреванию поверхности. Тепло, в свою очередь передается молекулам окружающего газа, в силу чего их движение, а, следовательно, и оказываемое ими давление возрастают, причем этот «радиометрический эффект» легко перекрывает искомое световое давление.
 Впервые преодолеть все экспериментальные трудности сумел П.Н. Лебедев. Идея опыта заключалась в том, что свет направлялся на одно из крылышек легкой вертушки, рис.10, причем ее поворот измерялся по отклонению зайчика, отбрасываемого маленьким, укрепленным на вертушке зеркальцем. Использование очень тонких крылышек привело к тому, что температура на обоих поверхностях была практически одинакова, что при малом давлении свело радиометрический эффект почти к нулю. Для зеркального крылышка
Впервые преодолеть все экспериментальные трудности сумел П.Н. Лебедев. Идея опыта заключалась в том, что свет направлялся на одно из крылышек легкой вертушки, рис.10, причем ее поворот измерялся по отклонению зайчика, отбрасываемого маленьким, укрепленным на вертушке зеркальцем. Использование очень тонких крылышек привело к тому, что температура на обоих поверхностях была практически одинакова, что при малом давлении свело радиометрический эффект почти к нулю. Для зеркального крылышка  ., а для зачерненного
., а для зачерненного  . Результаты, полученные Лебедевым в 1900 году, совпали с теоретическим значением (1.16) с точностью до 20%, что не выходило за рамки погрешности опыта. В 1907 году Лебедеву удалось решить еще более сложную задачу – доказать наличие светового давления на газы и даже измерить его. Давление света можно также объяснить, исходя из гипотезы световых фотонов (квантов энергии). Согласно гипотезе световых квантов Эйнштейна, свет испускается, распространяется и поглощается квантами – фотонами. Энергия кванта
. Результаты, полученные Лебедевым в 1900 году, совпали с теоретическим значением (1.16) с точностью до 20%, что не выходило за рамки погрешности опыта. В 1907 году Лебедеву удалось решить еще более сложную задачу – доказать наличие светового давления на газы и даже измерить его. Давление света можно также объяснить, исходя из гипотезы световых фотонов (квантов энергии). Согласно гипотезе световых квантов Эйнштейна, свет испускается, распространяется и поглощается квантами – фотонами. Энергия кванта  . Его массу можно найти из закона взаимосвязи массы и энергии
. Его массу можно найти из закона взаимосвязи массы и энергии  :
:
 (1.17)
(1.17)
Фотон – элементарная частица, которая движется всегда со скоростью света  (или
(или  , если свет распространяется в диспергирующей среде) и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и т.д., которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.
, если свет распространяется в диспергирующей среде) и имеет массу покоя, равную нулю. Следовательно, масса фотона отличается от массы таких элементарных частиц, как электрон, протон и т.д., которые обладают отличной от нуля массой покоя и могут находиться в состоянии покоя.
Импульс фотона  можно получить, если в общей формуле теории относительности положим массу покоя равной нулю (
можно получить, если в общей формуле теории относительности положим массу покоя равной нулю (  ):
):
 (1.18)
(1.18)
Если фотоны обладают импульсом, то свет, падающий на тело, должен оказывать на него давление. С точки зрения квантовой теории, давление света на поверхность обусловлено тем, что каждый фотон при соударении с поверхностью передает ей свой импульс.
Рассчитаем тогда световое давление, оказываемое на поверхность тела потоком монохроматического излучения с частотой  , падающего перпендикулярно поверхности. Если в единицу времени на единицу площади падает
, падающего перпендикулярно поверхности. Если в единицу времени на единицу площади падает  фотонов, то при коэффициенте отражения
фотонов, то при коэффициенте отражения  света от поверхности тела отразится
света от поверхности тела отразится  фотонов, а
фотонов, а  фотонов – поглотится. Каждый поглощенный фотон передает поверхности тела импульс
фотонов – поглотится. Каждый поглощенный фотон передает поверхности тела импульс  , а каждый отраженный -
, а каждый отраженный -  (поскольку при отражении импульс фотона изменяется в связи с изменением направления скорости на
(поскольку при отражении импульс фотона изменяется в связи с изменением направления скорости на  ). Давление света на поверхность равно импульсу, который передается поверхности за единицу времени
). Давление света на поверхность равно импульсу, который передается поверхности за единицу времени  фотонами:
фотонами:  . Энергия всех фотонов, падающих на единицу поверхности в единицу времени
. Энергия всех фотонов, падающих на единицу поверхности в единицу времени  , то есть освещенность поверхности, а
, то есть освещенность поверхности, а  - объемная плотность энергии излучения. Поэтому давление, производимое светом при нормальном падении на поверхность, будет равно:
- объемная плотность энергии излучения. Поэтому давление, производимое светом при нормальном падении на поверхность, будет равно:
 (1.19)
(1.19)
Формула (1.19), выведенная на основе кантовых представлений, совпадает с выражением, полученным из волновой теории Максвелла (1.16).
Эффект Комптона
Наиболее ярко корпускулярные свойства света проявляются в эффекте Комптона. Американский физик Комптон, изучая рассеяние монохроматических рентгеновских лучей на легких атомах (парафин, бор), обнаружил, что в составе рассеянного излучения наряду с излучением первоначальной длины волны наблюдается также излучение более длинных волн. Опыты показали, что разность  не зависит от длины волны
не зависит от длины волны  падающего излучения и природы рассеивающего вещества, а определяется только величиной угла рассеяния
падающего излучения и природы рассеивающего вещества, а определяется только величиной угла рассеяния  :
:
 (1.20)
(1.20)
где  - длина волны рассеянного излучения, а
- длина волны рассеянного излучения, а  - постоянная, называемая комптоновской длиной волны.
- постоянная, называемая комптоновской длиной волны.
Таким образом, можно определить эффект Комптона как упругое рассеяние коротковолнового электромагнитного излучения (рентгеновского или гамма-излучения) на свободных (или слабо связанных) электронах вещества, сопровождающееся возрастанием длины волны. Этот эффект не укладывается в рамки волновой теории, согласно которой длина волны при рассеянии изменяться не должна; под действием периодического поля световой волны электрон колеблется с частотой поля и поэтому излучает рассеянные волны той же частоты.
Исходя из квантовых представлений можно рассматривать эффект Комптона как результат упругого соударения рентгеновских фотонов со свободными электронами вещества (для легких атомов электроны слабо связаны с ядром, поэтому их можно считать в первом приближении свободными). В процессе этого столкновения фотон передает электрону часть своей энергии и импульса в соответствие с законами сохранения.
Рассмотрим упругое столкновение двух частиц – налетающего фотона, обладающего импульсом  и энергией
и энергией  , с покоящимся электроном, энергия покоя которого определяется
, с покоящимся электроном, энергия покоя которого определяется  . Фотон, столкнувшись с электроном, передает ему часть своей энергии и изменяет направление движения (рассеивается). Уменьшение энергии фотона и означает увеличение длины волны рассеянного излучения.
. Фотон, столкнувшись с электроном, передает ему часть своей энергии и изменяет направление движения (рассеивается). Уменьшение энергии фотона и означает увеличение длины волны рассеянного излучения.
 Пусть импульс и энергия рассеянного фотона соответственно равны
Пусть импульс и энергия рассеянного фотона соответственно равны  . Электрон, ранее покоившийся, приобретает импульс и энергию соответственно равные
. Электрон, ранее покоившийся, приобретает импульс и энергию соответственно равные  и приходит в движение – «испытывает отдачу», рис.11. При каждом таком столкновении должны, безусловно, выполняться законы сохранения энергии и импульса
и приходит в движение – «испытывает отдачу», рис.11. При каждом таком столкновении должны, безусловно, выполняться законы сохранения энергии и импульса
Согласно закону сохранения энергии:
 (1.21)
(1.21)
и согласно закону сохранения импульса:
 (1.22)
(1.22)
Согласно рис.11 можно записать по теореме косинусов:

умножив на с2, получим:
 (1.23)
(1.23)
из закона сохранения, возведя обе части в квадрат, получим:
 (1.24)
(1.24)
Раскрывая скобки и вычитая из (1.23) выражение (1.24), получим:

Используем общепринятое обозначение  . Тогда, учитывая, что
. Тогда, учитывая, что  , приходим к выражению:
, приходим к выражению:

отсюда получаем:

и, окончательно:
 , (1.25)
, (1.25)
где

Расчет дает, что  , что полностью совпадает с экспериментальными данными Комптона, а выражение (1.25) с выражением (1.20).
, что полностью совпадает с экспериментальными данными Комптона, а выражение (1.25) с выражением (1.20).
При взаимодействии фотонов с сильно связанными электронами, последние остаются в атоме и энергию и импульс отдачи получит атом как целое. Тогда в расчетах следует принимать не массу покоя электрона, а массу атома М0. Соответственно тогда изменение длины волны станет столь мало величиной (~10-15м), что для этой части рассеянного излучения длина волны рассеянного фотона практически совпадает с длиной волны падающего.
Корпускулярно-волновой дуализм, принцип дополнительности
Фотоэффект, эффект Комптона и другие эксперименты составили прочную основу фотонной (или корпускулярной) теории света. Но как быть с классическими опытами Юнга и других исследователей по интерференции и дифракции, доказавшими, что волновая теория света также имеет прочную экспериментальную основу.
Перед нами дилемма: одни эксперименты свидетельствуют о том, что свет ведет себя как волна, другие – что свет ведет себя как поток частиц. На первый взгляд кажется, что волновая и корпускулярная (фотонная) теории света несовместимы, но обе теории подтверждаются экспериментом. В конце концов, физики пришли к заключению, что двойственную природу света следует принять как непреложный факт. Именно эту двойственную природу света имеют в виду, когда говорят о корпускулярно-волновом дуализме. Ясно, что свет оказался более сложным явлением, чем просто волна или поток частиц.
Для выходы из этой ситуации великий датский физик Нильс Бор выдвинул свой знаменитый принцип дополнительности. Этот принцип утверждает, что для объяснения данного эксперимента следует использовать либо волновые, либо корпускулярные представления, но не те и другие одновременно. Однако для полного понимания природы света необходимо учитывать как волновые, так и корпускулярные свойства света. Оба этих аспекта взаимно дополняют друг друга.
Наглядно представить корпускулярно-волновой дуализм невозможно. Мы не в силах вообразить сочетание волновых свойств с корпускулярными. Следует осознать, что волновой и корпускулярный аспекты поведения света – это различные стороны его природы, проявляющиеся в экспериментах.
Отчасти трудности восприятия дуализма обусловлены особенностями нашего мышления. Наши зрительные образы (или модели) основаны на том, что мы видим в повседневной жизни. Мы применяем к свету понятия волны и частицы, поскольку опыт подсказывает нам, что в окружающем мире энергию переносят либо волны, либо частицы. Мы не можем непосредственно узреть, что представляет собой свет – волну или частицу, и полагаемся на косвенные эксперименты. Для трактовки этих экспериментов мы используем либо представление о волнах, либо представление о частицах. Но и то и другое – это абстракции нашего разума. Когда мы пытаемся постичь, что же такое свет «на самом деле», речь идет, в сущности, о наглядных представлениях. Между тем не существует причин, по которым природа света должна следовать одной из этих моделей (или зрительных образов), заимствованных из макроскопического мира. «Истинная» природа света (если подобное выражение имеет смысл) не поддается наглядной интерпретации. В лучшем случае мы лишь осознаем, что наше знание ограничено косвенными экспериментами и что свет на повседневном языке и в рамках обычных представлений обнаруживает свойства и волны, и частицы.
Следует подчеркнуть, что формула Эйнштейна  сама по себе связывает корпускулярные и волновые свойства света: энергия
сама по себе связывает корпускулярные и волновые свойства света: энергия  в левой части равенства относится к частице, а частота
в левой части равенства относится к частице, а частота  в правой части – к соответствующей волне.
в правой части – к соответствующей волне.
АТОМНАЯ ФИЗИКА
Вплоть до конца XIX века считалось, что атомы являются неделимыми частицами. Движение материи понималось как механическое перемещение этих частиц. Изменение химического состава - как взаимодействие атомов. К концу XIX века начали накапливаться сведения о свойствах атомов, указывающих на сложную их структуру.
При электрическом разряде в газе были обнаружены и исследованы катодные лучи, представляющие собой потоки отрицательно заряженных частиц, получивших название электронов. Было установлено, что атомы вырываются из атомов, которые при этом становятся положительно заряженными ионами. Измерение удельного заряда электронов и ионов показало, что масса электрона в тысячи раз меньше массы атомов. Во всех атомах имеются одинаковые по свойствам частицы вещества, несущие отрицательные заряды электроны. Положительный заряд оказался связанным с основной массой атома. Однако о распределении этого заряда внутри атома было неизвестно. Первую попытку создать модель атома предпринял Томпсон (1903 г.): атом - шар, равномерно заполненный положительным электрическим зарядом, внутри которого около положений своего равновесия колеблются электроны, рис.12. Однако в рамках этой модели невозможно объяснить наблюдаемые спектры, периодичность свойств атомов.
