Число ударов молекул о стенку

Рассмотрим находящийся в равновесии газ, заключенный в некотором сосуде. Допустим, что молекулы газа движутся только вдоль трех взаимно ┴ направлений. Это можно допустить из-за хаотичности движения молекул. Если в сосуде находится N молекул, то в любой момент времени вдоль каждого из направлений будет двигаться N/3 молекул и половина из них - N/6 вдоль данного направления в одну сторону, а вторая половина - в другую. Следовательно, в интересующем нас направлении по нормали к данному элементу ΔS стенки сосуда движется N/6 молекул, а для единицы объема - 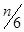, n – концентрация молекул.

Пусть все молекулы движутся с одинаковой средней скоростью <v>. За время Δt элемента стенки ΔS достигают все молекулы, находящиеся в параллелипипеде с площадью основания ΔS и длиной 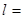<v>Δt. Их число Δν = (n/6)ΔS<v>Δt, следовательно, число ударов о единичную площадку в единицу времени

Δν/ΔSΔt = (n/6)<v>.

Если отказаться от допущения, что все молекулы движутся с одинаковой скоростью v = <v>, то необходимо выделить в единице объема молекулы, скорости которых лежат в интервале от v до v+dv. Количество таких молекул, долетающих до площадки ΔS за время Δt равно dν_v = (1/6)(dn_vΔ

vmax

SvΔt)

vmax

. Полное число ударов:

Δν = 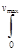dν_v = 1/6ΔSΔt 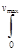vdn_v = Выражение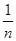 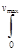vdn_v по определению является средней скоростью молекулы, тогда Δν = 1/6ΔSΔtn<v> , т.е., получили то же самое значение числа ударов.

Давление газа на стенку сосуда

Давление по определению можно записать: 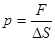, а поскольку, из второго закона Ньютона: 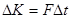, то 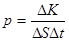. Значит, необходимо вычислить импульс 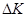, передаваемый всеми молекулами со всеми скоростями единице площади за единицу времени

Число молекул со скоростью v из общего количества n, долетающих до площадки ΔS за время Δt равно:

dν_v = (1/6)(dn_vΔSvΔt)

Далее, умножив это число на импульс, сообщаемый каждой молекулой при ударе равный – 2mv, получим импульс, сообщаемый площадке ΔS за время Δt этими молекулами. Изменение импульса одной молекулы равно (-2mv), значит, импульс передаваемый молекулой ст

vmax

енке равен +2mv.

vmax

Импульс, передаваемый всеми молекулами со всеми скоростями:

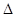K = 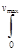(1/6)(dn_vΔSvΔt)2mv = 1/3ΔSΔtm 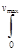v²dn_v (*)

Выражение 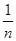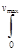v²dn_v представляет собой среднее значение квадрата скорости молекул, тогда, заменив в (*) интеграл и, разделив это выражение на ΔS и Δt, получим давление газа на стенку сосуда:

р = 1/3mn<v²>

т.к. m<v²>/2 = <ε_пост> по определению, получим:

р =2/3n<ε_пост>

- основное уравнение молекулярно- кинетической теории. Это уравнение раскрывает физический смысл макропараметра р: давление определяется средним значением кинетической энергии поступательного движения молекул.