Зависимость потенциальной энергии межмолекулярного взаимодействия от расстояния между молекулами
Зависимость сил межмолекулярного взаимодействия от расстояния между молекулами
Между молекулами вещества одновременно действуют силы притяжения и силы отталкивания. На расстоянии r = r0 сила F = 0, т. е. силы притяжения и отталкивания уравновешивают друг друга (см. рис.1). Таким образом, расстояние r0 соответствует равновесному состоянию между молекулами, на котором бы они находились в отсутствие теплового движения. При r < r0 преобладают силы отталкивания (Fo > 0), при г> г0 — силы притяжения (Fn < 0). На расстояниях г > 10-9 м межмолекулярные силы взаимодействия практически отсутствуют (F → 0).
Зависимость потенциальной энергии межмолекулярного взаимодействия от расстояния между молекулами
Элементарная работа δА силы F при увеличении расстояния между молекулами на dr совершается за счет уменьшения взаимной потенциальной энергии молекул, т. е. δA = F dr = - dП. Согласно рисунку б, если молекулы находятся друг от друга на расстоянии, на котором межмолекулярные силы взаимодействия не действуют (r →∞), то П = 0. При постепенном сближении молекул между ними появляются силы притяжения (F < 0), которые совершают положительную работу (δА = F dr > 0). Тогда потенциальная энергия взаимодействия уменьшается, достигая минимума при r = r0. При r < r0 с уменьшением r силы отталкивания (F > 0) резко возрастают и совершаемая против них работа отрицательна (δА = F dr < 0). Потенциальная энергия начинает тоже резко возрастать и становится положительной. Из данной потенциальной кривой следует, что система из двух взаимодействующих молекул в состоянии устойчивого равновесия (r = r0) обладает минимальной потенциальной энергией.
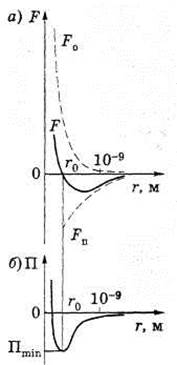 |
Рисунок 1 - Зависимость сил и потенциальной энергии межмолекулярного взаимодействия от расстояния между молекулами
Fo — сила отталкивания; Fu — сила притяжения; F — их равнодействующая
уравнение состояния идеального газа преобразуется в уравнение Ван-дер-Ваальса:
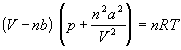 . (1.6)
. (1.6)
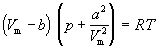 для одного моля газа
для одного моля газа
Изотермы
Проанализируем изотермы уравнения Ван–дер–Ваальса – зависимости Р от V для реального газа при постоянной температуре. Умножив уравнение Ван-дер-Ваальса на V2 и раскрыв скобки, получаем
PV3– (RT + bP) vV2+ av2V - abv3= 0.
Поскольку данное уравнение имеет третью степень относительно V, а коэффициенты при V действительны, то оно имеет либо один, либо три вещественных корня, т.е. изобара Р = const пересекает кривую Р = Р(V) в одной или трех точках, как это изображено на рисунке 7.4. Причем с повышением температуры мы перейдем от немонотонной зависимости Р = Р(V) к монотонной однозначной функции. Изотерма при Ткр, которая разделяет немонотонные T < Tкр и монотонные T > Ткр изотермы, соответствует изотерме при критической температуре. При температуре выше критической зависимость Р = Р(V) является однозначной монотонной функцией объема. Это означает, что при T > Ткр вещество находится только в одном, газообразном состоянии, как это имело место у идеального газа. При температуре газа ниже критической такая однозначность исчезает, а это означает возможность перехода вещества из газообразного в жидкое и наоборот. На участке АСВ изотермыТ1 давление растет с увеличением объема (dP/dV) > 0. Данное состояние неустойчиво, поскольку здесь должны усиливаться малейшие флуктуации плотности. Поэтому область ВСА не может устойчиво существовать. В областях DLBи AGEдавление падает с увеличением объема (dP/dV)Т< 0 – это необходимое, но не достаточное условие устойчивого равновесия. Эксперимент показывает, что система переходит из области устойчивых состояний GE (газ) в область устойчивых состояний LD (жидкость) через двухфазное состояние (газ – жидкость)GL вдоль горизонтальной изотермы GCL.
При квазистатическом сжатии, начиная с точки G, система распадается на 2 фазы – жидкость и газ, причем плотности жидкости и газа остаются при сжатии неизменными и равными их значениям в точках L и Gсоответственно. При сжатии количество вещества в газообразной фазе непрерывно уменьшается, а в жидкой фазе – увеличивается, пока не будет достигнута точка L, в которой все вещество перейдет в жидкое состояние.
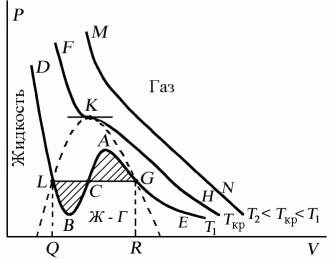
Рис. 7.4
Наличие критической точки на изотерме Ван–дер–Ваальса означает, что для каждой жидкости существует такая температура, выше которой вещество может существовать только в газообразном состоянии. К этому заключению пришел и Д.И. Менделеев в 1861 г. Он заметил, что при определенной температуре прекращалось поднятие жидкости в капиллярах, т.е. поверхностное натяжение обращалось в нуль. При той же температуре обращалась в нуль скрытая теплота парообразования. Такую температуру Менделеев назвал температурой абсолютного кипения. Выше этой температуры, согласно Менделееву, газ не может быть сконденсирован в жидкость никаким увеличением давления.
Критическую точку K мы определили как точку перегиба критической изотермы, в которой касательная к изотерме горизонтальна (рис. 7.5). Ее можно определить также как точку, в которую в пределе переходят горизонтальные участки изотерм при повышении температуры до критической. На этом основан способ определения критических параметров Pk, Vk, Тk, принадлежащий Эндрюсу. Строится система изотерм при различных температурах. Предельная изотерма, у которой горизонтальный участок LG (рис. 7.4) переходит в точку, будет критической изотермой, а указанная точка – критической точкой (рис. 7.5).
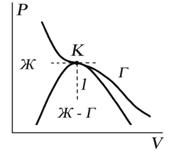
Рис. 7.5
Недостаток способа Эндрюса заключается в его громоздкости.
