Методика измерения диэлектрической проницаемости

ОПРЕДЕЛЕНИЕ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ПОЛУПРОВОДНИКОВ

ВИРТУАЛЬНАЯ ЛАБОРАТОРНАЯ РАБОТА №3 ПО

ФИЗИКЕ ТВЕРДОГО ТЕЛА

Методические указания к выполнению лабораторной работы №3 по разделу физики «Твердого тела» для студентов технических специальностей всех форм обучения

Красноярск 2012

УДК 539.194

Рецензент

Кандидат физико-математических наук, доцент О.Н. Бандурина

(Сибирский государственный аэрокосмический университет

имени академика М.Ф. Решетнева)

Печатается по решению методической комиссии ИКТ

Определение диэлектрической проницаемости полупроводников. Виртуальная лабораторная работа №3 по физике твердого тела: Методические указания к выполнению лабораторной работы №3 по разделу физики «Твердого тела» для студентов техн. спец. всех форм обучения / сост.: А.М. Харьков; Сиб. гос. аэрокосмич. ун-т. – Красноярск, 2012. – 21 с.

Сибирский государственный аэрокосмический

университет имени академика М.Ф. Решетнева, 2012

СОДЕРЖАНИЕ

Введение……………………………………………………………………………...4

Допуск к лабораторной работе……………………………………………………...4

Оформление лабораторной работы к защите……………………………………...4

Определение диэлектрической проницаемости полупроводников…………........5

Теория метода……………………………………………………………………......5

Методика измерения диэлектрической проницаемости…………………..……..11

Обработка результатов измерений………………………..………………………16

Контрольные вопросы…………..………………………………………………….17

Тест………………………………………………………………………………….17

Список литературы…………………………………………………………………20

Приложение…………………………………………………………………………21

ВВЕДЕНИЕ

Данные методические указания содержат описания к лабораторным работам, в которых используются виртуальные модели из курса «Физика твердого тела».

Допуск к лабораторной работе:

Проводится преподавателем по группам с персональным опросом каждого студента. Для допуска:

1) Каждый студент предварительно оформляет свой персональный конспект данной лабораторной работы;

2) Преподаватель индивидуально проверяет оформление конспекта и задает вопросы по теории, методике измерений, установке и обработке результатов;

3) Студент отвечает на заданные вопросы;

4) Преподаватель допускает студента к работе и ставит свою подпись в конспекте студента.

Оформление лабораторной работы к защите:

Полностью оформленная и подготовленная к защите работа должна соответствовать следующим требованиям:

Выполнение всех пунктов: все расчеты требуемых величин, заполнены чернилами все таблицы, построены все графики и т.д.

Графики должны удовлетворять всем требованиям преподавателя.

Для всех величин в таблицах должна быть записана соответствующая единица измерения.

Записаны выводы по каждому графику.

Выписан ответ по установленной форме.

Записаны выводы по ответу.

ОПРЕДЕЛЕНИЕ ДИЭЛЕКТРИЧЕСКОЙ ПРОНИЦАЕМОСТИ ПОЛУПРОВОДНИКОВ

Теория метода

Поляризация – это способность диэлектрика под действием электрического поля поляризоваться, т.е. изменять в пространстве расположение связанных заряженных частиц диэлектрика.

Важнейшим свойством диэлектриков является их способность к электрической поляризации, т.е. под влиянием электрического поля происходит направленное смещение заряженных частиц или молекул на ограниченное расстояние. Под действие электрического поля смещаются заряды, как в полярных, так и неполярных молекулах.

Существует более десятка различных видов поляризации. Рассмотрим некоторые из них:

1. Электронная поляризация – это смещение электронных орбит относительно положительно заряженного ядра. Оно происходит во всех атомах любого вещества, т.е. во всех диэлектриках. Электронная поляризация устанавливается за время 10^-15–10^-14с.

2. Ионная поляризация – смещение относительно друг друга разноименно заряженных ионов в веществах с ионными связями. Время ее установления 10^-13 –10^-12с. Электронная и ионная поляризация относятся к числу мгновенных или деформационных видов поляризации.

3. Дипольная или ориентационная поляризация обусловлена ориентацией диполей в направлении электрического поля. Дипольной поляризацией обладают полярные диэлектрики. Время ее установления 10^-10–10^-6с. Дипольная поляризация относится к числу медленных или релаксационных видов поляризации.

4. Миграционная поляризация наблюдается в неоднородных диэлектриках, в которых электрические заряды накапливаются на границе радела неоднородностей. Процессы установления миграционной поляризации очень медленны и могут протекать на протяжении минут и даже часов.

5. Ионно-релаксационная поляризация обусловлена избыточным перебросом слабо связанных ионов под действием электрического поля на расстояния, превышающие постоянную решетки. Ионно-релаксационная поляризация проявляется в некоторых кристаллических веществах при наличии в них примесей в виде ионов или неплотной упаковке кристаллической решетки. Время ее установления 10^-8–10^-4с.

6. Электронно-релаксационная поляризация возникает за счет возбужденных тепловой энергией избыточных «дефектных» электронов или «дырок». Этот вид поляризации, как правило, обуславливает высокое значение диэлектрической проницаемости.

7. Спонтанная поляризация – самопроизвольная поляризация, возникающая в некоторых веществах (например, сегнетовой соли) в определенной области температур.

8. Упруго-дипольная поляризация связана с упругим поворотом диполей на небольшие углы.

9. Остаточная поляризация – поляризация, которая остается в некоторых веществах (электретах) в течение продолжительного времени после снятия электрического поля.

10. Резонансная поляризация. Если частота электрического поля близка к собственной частоте колебаний диполей, то колебания молекул могут возрасти, что приведет к появлению резонансной поляризации в дипольном диэлектрике. Резонансная поляризация наблюдается при частотах лежащих в области инфракрасного света. Реальный диэлектрик может одновременно обладать несколькими видами поляризации. Возникновение того или иного вида поляризации определяется физико-химическими свойствами вещества и диапазоном используемых частот [5].

Основные параметры:

ε – диэлектрическая проницаемость – мера способности материала к поляризации; это величина, показывающая во сколько раз сила взаимодействия электрических зарядов в данном материале меньше, чем в вакууме. Внутри диэлектрика возникает поле, направленное противоположно внешнему.

Напряженность внешнего поля ослабевает по сравнению с полем тех же зарядов в вакууме в ε раз, где ε – относительная диэлектрическая проницаемость.

Если вакуум между обкладками конденсатора заменяется на диэлектрик, то в результате поляризации емкость возрастает. На этом основано простое определение диэлектрической проницаемости:

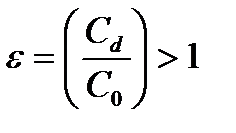(1)

где C₀ – емкость конденсатора, между обкладками которого – вакуум.

C_d – емкость того же конденсатора с диэлектриком.

Диэлектрическая проницаемость ε изотропной среды определяется отношением:

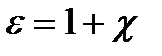(2)

где χ – диэлектрическая восприимчивость.

D = tg δ – тангенс угла диэлектрических потерь

Диэлектрические потери – потери электрической энергии, обусловленные протеканием токов в диэлектриках. Различают ток сквозной проводимости I_ск.пр, вызванный наличием в диэлектриках небольшого количества легкоподвижных ионов, и поляризационные токи. При электронной и ионной поляризации поляризационный ток называется током смещения I_см, он очень кратковременный и не регистрируется приборами. Токи, связанные с замедленными (релаксационными) видами поляризации, называются токами абсорбции I_абс. В общем случае суммарный ток в диэлектрике определяется как: I=I_абс+I_ск.пр. После установления поляризации суммарный ток будет равен: I=I_ск.пр. Если в постоянном поле поляризационные токи возникают в момент включения и выключения напряжения, и суммарный ток определяется в соответствии с уравнением: I=I_ск.пр, то в переменном поле поляризационные токи возникают в момент смены полярности напряжения. Вследствие этого потери в диэлектрике в переменном поле могут быть значительными, особенно если полупериод приложенного напряжения приближается к времени установления поляризации.

На рис. 1(a) приведена схема, эквивалентная конденсатору с диэлектриком, находящемуся в цепи переменного напряжения. В этой схеме конденсатор с реальным диэлектриком, который обладает потерями, заменен идеальным конденсатором C с параллельно включенным активным сопротивлением R. На рис. 1(б) приведена векторная диаграмма токов и напряжений для рассматриваемой схемы, где U – напряжения в цепи; I_ак – активный ток; I_р – реактивный ток, который опережает по фазе на 90° активную составляющую; I_∑ - суммарный ток. При этом: I_а=I_R=U/R и I_р=I_C=ωCU, где ω – круговая частота переменного поля.

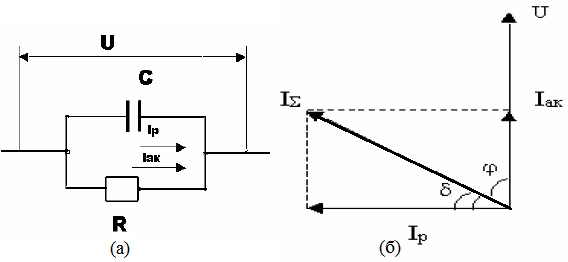
Рис. 1. (а) – схема; (б) – векторная диаграмма токов и напряжений

Углом диэлектрических потерь называется угол δ, дополняющий до 90° угол сдвига фаз φ между током I_∑ и напряжением U в емкостной цепи. Потери в диэлектриках в переменном поле характеризуются тангенсом угла диэлектрических потерь: tg δ=I_а/I_р.

Предельные значения тангенса угла диэлектрических потерь для высокочастотных диэлектриков не должны превышать (0,0001 – 0,0004), а для низкочастотный – (0,01 – 0,02).

Зависимости ε и tg δ от температуры T и частоты ω

Диэлектрические параметры материалов в различной степени зависят от температуры и частоты. Большое количество диэлектрических материалов не позволяет охватить особенности всех зависимостей от указанных факторов.

Поэтому на рис. 2 (a, б) изображены общие тенденции, характерные для некоторых основных групп т.е. приведены типичные зависимости диэлектрической проницаемости ε от температуры T (а) и от частоты ω (б).

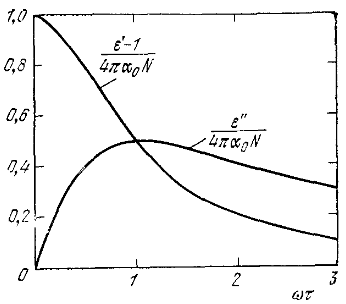
Рис. 2. Частотная зависимость действительной (εʹ) и мнимой (εʺ) частей диэлектрической проницаемости при наличии ориентационного механизма релаксации

Комплексная диэлектрическая проницаемость.При наличии процессов релаксации диэлектрическую проницаемость удобно записывать в комплексном виде. Если для поляризуемости справедлива формула Дебая:

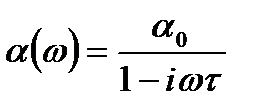(3)

где, τ – время релаксации, α₀ – статистическая ориентационная поляризуемость. То, полагая локальное поле равным внешнему, получим (в СГС):

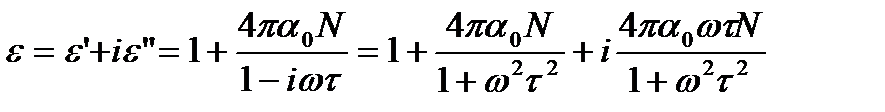(4)

Графики зависимости εʹ и εʺ от произведения ωτ приведены на рис. 2. Заметим, что уменьшение εʹ (действительной части ε) имеет место вблизи максимума εʺ (мнимой части ε).

Такой ход изменения εʹ и εʺ с частотой служит частым примером более общего результата, согласно которому εʹ(ω) от частоты влечет за собой также и зависимость εʺ(ω) от частоты. В системе СИ следует заменить 4π на 1/ε₀.

Под действием приложенного поля молекулы в неполярном диэлектрике поляризуются, становясь диполями с индуцированным дипольным моментом μ_и, пропорциональным напряженности поля:

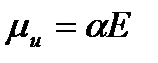(5)

В полярном диэлектрике дипольный момент полярной молекулы μ в общем случае равен векторной сумме собственного μ₀ и индуцированного μ_и моментов:

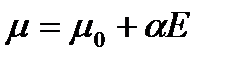(6)

Напряженности поля, создаваемого этими диполями, пропорциональны дипольному моменту и обратно пропорциональны кубу расстояния.

Для неполярных материалов обычно ε = 2 – 2,5 и не зависит от частоты до ω ≈10¹²Hz. Зависимость ε от температуры обусловлена у них тем, что при ее изменении изменяются линейные размеры твердых и объемы жидких и газообразных диэлектриков, что изменяет число молекул n в единице объема

и расстояния между ними. Используя известные из теории диэлектриков соотношения F=n\μ_и и F=ε₀(ε-1)Е, где F – поляризованность материала, для неполярных диэлектриков имеем:

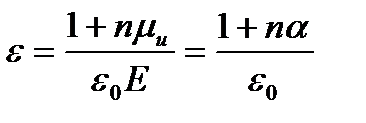(7)

При E=const также μ_и = const и температурное изменение ε обусловлено только изменением n, которое является линейной функцией температуры Θ, зависимость ε = ε(Θ) также является линейной. Для полярных диэлектриков аналитических зависимостей нет, и обычно пользуются эмпирическими.

1)С возрастанием температуры объем диэлектрика увеличивается и диэлектрическая проницаемость немного уменьшается. Особенно заметно уменьшение ε в период размягчения и плавления неполярных диэлектриков, когда их объем существенно возрастает. Ввиду высокой частоты обращения электронов на орбитах (порядка 10¹⁵–10¹⁶Hz) время установления равновесного состояния электронной поляризации очень мало и проницаемость ε неполярных диэлектриков не зависит от частоты поля в обычно используемом диапазоне частот (до 10¹²Hz).

2) При повышении температуры ослабевают связи между отдельными ионами, что облегчает их взаимодействие под действием внешнего поля и это приводит к увеличению ионной поляризации и диэлектрической проницаемости ε. Ввиду малости времени установления состояния ионной поляризации (порядка 10¹³Hz, что соответствует собственной частоте колебания ионов в кристаллической решетке) изменение частоты внешнего поля в обычных рабочих диапазонах практически не отражается на величине ε в ионных материалов.

3) Диэлектрическая проницаемость полярных диэлектриков сильно зависит от температуры и частоты внешнего поля. С возрастанием температуры увеличивается подвижность частиц и уменьшается энергия взаимодействия между ними, т.е. облегчается их ориентация под действием внешнего поля – возрастает дипольная поляризация и диэлектрическая проницаемость. Однако этот процесс продолжается лишь до определенной температуры. При дальнейшем возрастании температуры проницаемость ε уменьшается. Так как ориентация диполей по направлению поля осуществляется в процессе теплового движения и посредством теплового движения, то установление поляризации требует значительного времени. Это время настолько велико, что в переменных полях высокой частоты диполи не успевают ориентироваться по полю, и проницаемость ε падает [3].

Методика измерения диэлектрической проницаемости

Емкость конденсатора. Конденсатор – это система из двух проводников (обкладок), разделенных диэлектриком, толщина которого мала по сравнению с линейными размерами проводников. Так, например, две плоские металлические пластины, расположенные параллельно и разделенные слоем диэлектрика, образуют конденсатор (рис. 3).

Если пластинам плоского конденсатора сообщить равные по модулю заряды противоположного знака, то напряженность электрического поля между пластинами будет в два раза больше, чем напряженность поля у одной пластины:

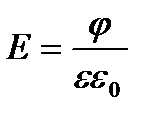(8)

где ε – диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Физическая величина, определяемая отношением заряда q одной из пластин конденсатора к разности потенциалов Δφ между обкладками конденсатора, называется электроемкостью конденсатора:

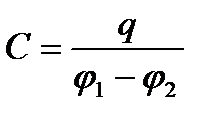(9)

Единица электроемкости СИ – Фарад (Ф). Емкостью в 1 Ф обладает такой конденсатор, разность потенциалов между обкладками которого равна 1 В при сообщении обкладкам разноименных зарядов по 1 Кл: 1 Ф = 1 Кл/1 В.

Емкость плоского конденсатора. Формулу для вычисления электроемкости плоского конденсатора можно получить, используя выражение (8). В самом деле, напряженность поля: Е = φ/εε₀ = q/εε₀S, где S – площадь пластины. Поскольку поле однородное, то разность потенциалов между обкладками конденсатора равна: φ₁ – φ₂ = Еd = qd/εε₀S, где d – расстояние между обкладками. Подставив в формулу (9), получим выражение для электроемкости плоского конденсатора:

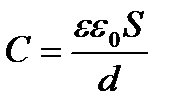(10)

где ε₀ – диэлектрическая проницаемость воздуха; S – площадь пластины конденсатора, S=hl, где h – ширина пластины, l – ее длина; d – расстояние между пластинами конденсатора.

Выражение (10) показывает, что электроемкость конденсатора можно увеличить путем увеличения площади S его обкладок, уменьшения расстояния d между ними и применения диэлектриков с большими значениями диэлектрической проницаемости ε [4].

Рис. 3. Конденсатор с помещенным в него диэлектриком

Если между пластинами конденсатора поместить пластину из диэлектрика, емкость конденсатора изменится. Следует рассмотреть вариант расположения диэлектрической пластины между пластинами конденсатора.

Обозначим: d_в – толщину воздушного промежутка, d_м – толщину диэлектрической пластины, l_В – длину воздушной части конденсатора, l_м – длину части конденсатора, заполненной диэлектриком, ε_м – диэлектрическую проницаемость материала. Если учесть, что l = l_в+ l_м, а d = d_в + d_м, то эти варианты можно рассмотреть для случаев:

В случае l_в = 0, d_в = 0 мы имеем конденсатор с твердым диэлектриком:

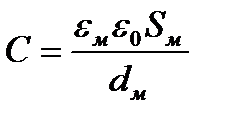(11)

Из уравнений классической макроскопической электродинамики, основанной на уравнениях Максвелла следует, что при помещении диэлектрика в слабое переменное поле, изменяющееся по гармоническому закону с частотой ω, тензор комплексной диэлектрической проницаемости приобретает вид:

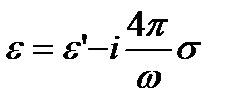(12)

где σ – оптическая проводимость вещества, εʹ – диэлектрическая проницаемость вещества, связанная с поляризацией диэлектрика. Выражение (12) можно привести к следующему виду:

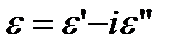(13)

где мнимое слагаемое отвечает за диэлектрические потери [1].

На практике измеряют С – емкость образца, имеющего форму плоского конденсатора. Этот конденсатор характеризуется тангенсом угла диэлектрических потерь:

tgδ=ωCR_c (14)

или добротностью:

Q_c =1/ tgδ (15)

где R_c – сопротивление, зависящее, главным образом, от диэлектрических потерь. Для измерения этих характеристик существует ряд методов: различные мостовые методы, измерения с преобразованием измеряемого параметра во временной интервал и т.д. [2].

При измерениях емкости С и тангенса угла диэлектрических потерь D = tgδ в данной работе была использована методика, разработанная кампанией GOOD WILL INSTRUMENT Со Ltd. Измерения проведены на прецизионном измерителе иммитанса – LCR-819-RLC. Прибор позволяет измерять емкость в пределах 20 pF–2,083 mF, тангенс угла потерь в пределах 0,0001-9999 и подавать поле смещения. Внутреннее смещение до 2 В, внешнее смещение до 30 В. Точность измерений составляет 0,05 %. Частота тест-сигнала 12 Hz -100 kHz.

В этой работе измерения проведены на частоте 1 kHz в интервале температур 77 К < T < 270 К в нулевом магнитном поле и в поле 5 kOe. Образцы для измерений имели форму параллелепипеда с размерами 2*3*4 мм (х=0.1), где d = 2 мм – толщина образца, площадь грани S = 3*4 мм².

С целью получений температурных зависимостей ячейка с образцом помещается в поток хладагента (азота) пропускаемый через теплообменник, температура которого задается нагревателем. Температура нагревателя контролируется терморегулятором. Обратная связь с измерителя температуры на терморегулятор позволяет задавать скорость измерения температуры, либо осуществлять ее стабилизацию. Для контроля температуры используется термопара. В данной работе температура изменялась со скоростью 1 град/мин. Указанный метод позволяет измерять температуру с погрешностью 0,1 град.

Измерительная ячейка с закрепленным на ней образцом помещается в проточный криостат. Связь ячейки с LCR-метром осуществляется экранированными проводами через разъем в капке криостата. Криостат размещен между полюсами электромагнита ФЛ-1. Блок питания магнита позволяет получать магнитные поля до 15 kOe. Для измерения величины напряженности магнитного поля Н используется термостабилизированный датчик Холла с блоком электроники. Для стабилизации магнитного поля между блоком питания и измерителем магнитного поля существует обратная связь.

Измеренные значения емкости С и тангенса угла потерь D = tg δ связаны со значениями искомых физических величин εʹ и εʺ следующими соотношениями:

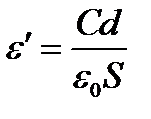(16)

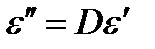(17)

№	C (pF)	Re (ε’)	T (°К)	tg δ	Qc	Im (ε”)	ω (Hz)	σ (ω)
	3,805	71,66		0,075	13,33	5,375	103
	3,838			0,093
	3,86			0,088
	3,849			0,094
	3,893			0,106
	3,917			0,092
	3,951			0,103
	3,824			0,088
	3,873			0,105
	3,907			0,108
	3,977			0,102
	4,031			0,105
	4,062			0,132
	4,144			0,109
	4,24			0,136
	4,435			0,175
	4,553			0,197
	4,698			0,233
	4,868			0,292
	4,973			0,361
	5,056			0,417
	5,164			0,491
	5,246			0,552
	5,362			0,624
	5,453			0,703
	5,556			0,783
	5,637			0,867
	5,738			0,955
	5,826			1,04
	5,902			1,136

Таблица №1. Gd_xMn_1-xS, (x=0.1).