Соответствие между параметрами двумерного сигнала в пространственной и частотной областях
Очевидно, существует определенное соответствие между элементами энергетического спектра и сингулярными тройками матрицы исходного цифрового сигнала.
Определение.Назовем
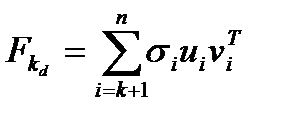
дополнением к аппроксимации 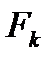 ,
,
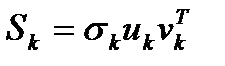
 -й составляющей изображения
-й составляющей изображения 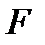 .
.
На примере изображения CAMERAMAN рассмотрим аппроксимации различного ранга, а также дополнения к аппроксимациям (рис.2.3). Результаты визуально аналогичны результатам низкочастотной (рис.2.3(б,в)) и высокочастотной фильтрации (рис.2.3(д,е)). Варианты а и г (рис.2.3) зрительно не отличаются друг от друга.

Рис.2.3. Изображение CAMERAMAN и его аппроксимации: исходное изображение (а); 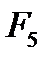 (б);
(б); 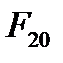 (в);
(в); 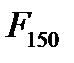 (г);
(г); 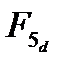 (д);
(д); 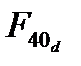 (е)
(е)
Легко предположить, что сингулярные тройки, соответствующие наименьшим СНЧ матрицы исходного изображения, отсутствующие в 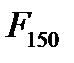 , отвечают, главным образом, высокочастотным составляющим исходного изображения (основной вклад в энергию сигнала вносят его низкочастотные составляющие).
, отвечают, главным образом, высокочастотным составляющим исходного изображения (основной вклад в энергию сигнала вносят его низкочастотные составляющие).
Исходя из рассмотренных результатов, выдвигается следующая гипотеза: сингулярные тройки, отвечающие наибольшим СНЧ, соответствуют, главным образом, низкочастотным, а наименьшим — высокочастотным составляющим сигнала.
Для проверки гипотезы в среде Matlab был проведен вычислительный эксперимент, в котором использовались 300 различных по размерности, яркости, текстуре и т.д. изображений в градациях серого. Для наглядности иллюстрации основных результатов рассмотрим в качестве исходного изображения главную подматрицу 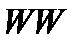 матрицы
матрицы 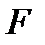 изображения POUT размера
изображения POUT размера 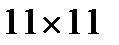 , дающую типичную качественную картину. Будем обозначать матрицу центрированного энергетического спектра произвольной матрицы
, дающую типичную качественную картину. Будем обозначать матрицу центрированного энергетического спектра произвольной матрицы 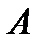 как
как 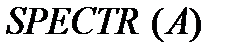 . Рассмотрим для
. Рассмотрим для 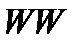 центрированные энергетические спектры некоторых ее составляющих, аппроксимаций и дополнений к аппроксимациям (рис.2.4 — выделены наибольшие и наименьшие значения спектральных коэффициентов). Как видно из приведенных результатов, сингулярные тройки, отвечающие максимальным СНЧ, соответствуют низкочастотным составляющим сигнала-изображения. По мере уменьшения СНЧ, происходит подключение средних и высоких частот, а вклад низких становится все меньше. Наименьшие СНЧ отвечают высокочастотным составляющим двумерного цифрового сигнала.
центрированные энергетические спектры некоторых ее составляющих, аппроксимаций и дополнений к аппроксимациям (рис.2.4 — выделены наибольшие и наименьшие значения спектральных коэффициентов). Как видно из приведенных результатов, сингулярные тройки, отвечающие максимальным СНЧ, соответствуют низкочастотным составляющим сигнала-изображения. По мере уменьшения СНЧ, происходит подключение средних и высоких частот, а вклад низких становится все меньше. Наименьшие СНЧ отвечают высокочастотным составляющим двумерного цифрового сигнала.
Проверим, как реагирует энергетический спектр исходного изображения 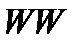 на возмущения различных СНЧ. При проведении вычислительного эксперимента возмущения наибольших СНЧ приводили к возмущениям в центральной части матрицы спектра, оставляя практически неизменными высокочастотные составляющие. При возмущении малых СНЧ, картина менялась на противоположную: значительно возмущались высокочастотные составляющие энергетического спектра и практически не затрагивались другие частотные составляющие. Например, если значение
на возмущения различных СНЧ. При проведении вычислительного эксперимента возмущения наибольших СНЧ приводили к возмущениям в центральной части матрицы спектра, оставляя практически неизменными высокочастотные составляющие. При возмущении малых СНЧ, картина менялась на противоположную: значительно возмущались высокочастотные составляющие энергетического спектра и практически не затрагивались другие частотные составляющие. Например, если значение 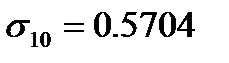 положить равным 0.0008, матрица относительных возмущений (погрешностей) каждого элемента центрированного энергетического спектра, вычисленных в процентах, будет иметь вид (жирным шрифтом выделены максимальные относительные погрешности):
положить равным 0.0008, матрица относительных возмущений (погрешностей) каждого элемента центрированного энергетического спектра, вычисленных в процентах, будет иметь вид (жирным шрифтом выделены максимальные относительные погрешности):
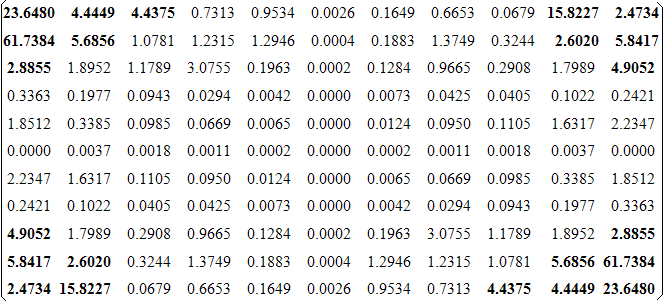

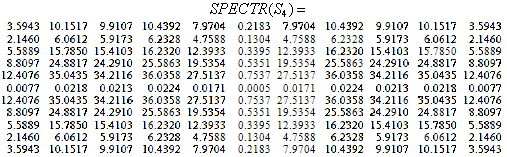
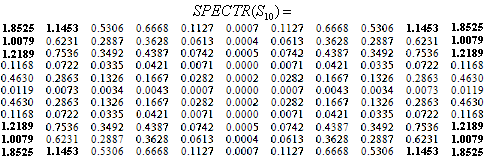
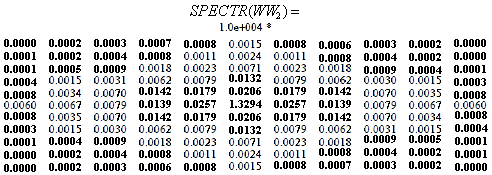

Рис.2.4. Матрицы центрированных энергетических спектров
Таким образом, результаты эксперимента полностью подтверждают выдвинутую гипотезу.
