Свойства частиц и взаимодействий 8 страница
| 3) | 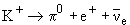 | ||
| Qадр: | 1  0 0 |  Qадр = -1 Qадр = -1 | |
| S: | 1  0 0 |  S = -1 S = -1 | |
| I3: | ½  0 0 |  I3 = -1/2 I3 = -1/2 | |
| Le: | 0  0 - 1 - 1 0 - 1 - 1 |  Le = -2 Le = -2 |
Распад запрещен законом сохранения лептонного числа Le.
| 4) | 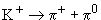 | ||
| Qадр: | 1  1 + 0 1 + 0 |  Qадр = -1 Qадр = -1 | |
| S: | 1  0 + 0 0 + 0 |  S = -1 S = -1 | |
| I3: | ½  1 + 0 1 + 0 |  I3 = 1/2 I3 = 1/2 |
Распад разрешен - выполнены все законы сохранения для слабого взаимодействия. Диаграмма этого распада:

16. Диаграммы показывают два варианта взаимодействия красного и зеленого кварков. Определить, за счет какого взаимодействия произошла реакция в каждом случае и что было виртуальной частицей.
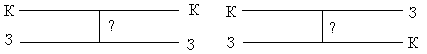
В первом случае при взаимодействии двух кварков их цвет не изменяется. Это возможно, либр в сильном взаимодействии при обмене глюоном со скрытым цветом (К  , З
, З  , С
, С  ), либо в электрослабом взаимодействии, когда виртуальными частицами являются не имеющие цвета фотон и Z-бозон. Наиболее вероятен вариант сильного взаимодействия с обменом глюоном, имеющим скрытый цвет.
), либо в электрослабом взаимодействии, когда виртуальными частицами являются не имеющие цвета фотон и Z-бозон. Наиболее вероятен вариант сильного взаимодействия с обменом глюоном, имеющим скрытый цвет.
Во втором случае цвет кварков изменился. Это возможно, только если взаимодействие между кварками сильное, и, следовательно, виртуальной частицей является глюон.
17. Показать, что пространственная четность позитрония (e+e- ) равна (-1)L+1, где L - относительный орбитальный момент e+ и e-.
Пространственная четность позитрония Pпоз определяется как произведение внутренней четности электрона и позитрона на орбитальный множитель (-1)L. Электрон и позитрон имеют значения спинов равные 1/2 и, следовательно, являются соответственно фермионом и антифермионом. Произведение внутренних четностей электрона и позитрона равна (-1), поскольку внутренняя четность фермиона противоположна внутренней четности антифермиона. Пространственная четность позитрония
Pпоз = (-1)(-1)L = (-1)L+1.
18. Какие значения может иметь относительный орбитальный момент двух 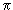 0-мезонов, образующихся в реакции
0-мезонов, образующихся в реакции 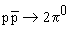 , если относительный орбитальный момент
, если относительный орбитальный момент 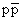 равен L?
равен L?
Относительный орбитальный момент двух 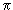 0-мезонов l определим из законов сохранения момента количества движения и четности. Получаем соотношение
0-мезонов l определим из законов сохранения момента количества движения и четности. Получаем соотношение
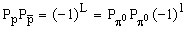
где 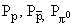 - внутренние четности протона, антипротона и
- внутренние четности протона, антипротона и  0-мезона. Внутренние четности протона
0-мезона. Внутренние четности протона 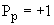 , антипротона
, антипротона 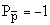 и
и  0-мезона
0-мезона 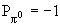 . Получаем, что (-1)(-1)L = (-1)l, то есть l = L + 1.
. Получаем, что (-1)(-1)L = (-1)l, то есть l = L + 1.
19. Как доказать несохранение четности в распаде 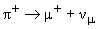 ?
?
Спиральность частицы есть
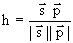 ,
,
где  - спин частицы, а
- спин частицы, а 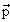 - ее импульс.
- ее импульс.
Состояние, при котором направления спина и импульса совпадают, соответствуют спиральности h = +1, а состояние с противоположно направленными спином и импульсом соответствует спиральности h = -1. Ультрарелятивистские фермионы, участвующие в любом слабом процессе, должны иметь значение спиральности h = -1 для частиц и h = +1 для античастиц.
Пион 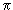 + имеет спин, равный 0. При распаде
+ имеет спин, равный 0. При распаде 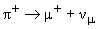 мюонное нейтрино как ультрарелятивистская частица будет обладать спиральностью h = -1. Соответственно, мюон, согласно законам сохранения импульса и момента импульса, также будет иметь спиральность равную h = -1. Хотя мюон и является античастицей, но в данном распаде его кинетическая энергия значительно меньше его массы покоя, так как
мюонное нейтрино как ультрарелятивистская частица будет обладать спиральностью h = -1. Соответственно, мюон, согласно законам сохранения импульса и момента импульса, также будет иметь спиральность равную h = -1. Хотя мюон и является античастицей, но в данном распаде его кинетическая энергия значительно меньше его массы покоя, так как 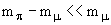 , и, следовательно, мюон нельзя считать релятивистским. Такой мюон может иметь спиральность h = -1.
, и, следовательно, мюон нельзя считать релятивистским. Такой мюон может иметь спиральность h = -1.
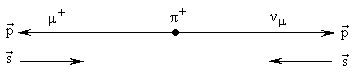
Применение к этому распаду операции пространственной инверсии приводит к тому, что нейтрино будет иметь спиральность h = +1, что невозможно для ультрарелятивистского фермиона. Отсутствие симметрии данного распада относительно пространственной инверсии указывает на несохранение пространственной четности в слабых взаимодействиях.
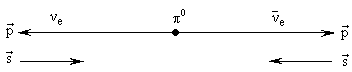
20. Возможен ли распад  0
0 
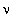 e +
e +  e для нейтрино с нулевой массой?
e для нейтрино с нулевой массой?
Нейтрино всегда имеет отрицательную спиральность, а антинейтрино всегда имеет положительную спиральность.
Спин нейтрино 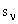 равен 1/2, и направление его вектора противоположно направлению движения частицы. Спин антинейтрино
равен 1/2, и направление его вектора противоположно направлению движения частицы. Спин антинейтрино 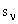 также равен 1/2, но направление его вектора совпадает с направлением движения частицы.
также равен 1/2, но направление его вектора совпадает с направлением движения частицы.
При распаде, исходя из закона сохранения импульса, нейтрино должны разлетаться строго в противоположные стороны. Момент количества движения 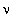 e и
e и  e
e 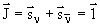 . Однако, спин
. Однако, спин  0-мезона равен 0, то есть данный распад невозможен из-за нарушения закона сохранения момента количества движения
0-мезона равен 0, то есть данный распад невозможен из-за нарушения закона сохранения момента количества движения 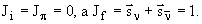
21. Почему распад 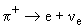 сильно (в 104 раз) подавлен по сравнению с распадом
сильно (в 104 раз) подавлен по сравнению с распадом 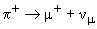 хотя энерговыделение в распаде
хотя энерговыделение в распаде 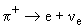 во много раз больше, чем в распаде
во много раз больше, чем в распаде 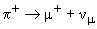 ?
?
Ультрарелятивистские фермионы, участвующие в любом слабом процессе, должны иметь значение спиральности h = -1 для частиц и h = +1 для античастиц.
В указанных распадах нейтрино будут обладать спиральностью h = -1. Поэтому из закона сохранения момента импульса следует, что спин 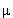 + должен быть направлен против его импульса.
+ должен быть направлен против его импульса. 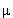 +-мезон образовался в результате слабого взаимодействия, и, следовательно, он должен был бы иметь h(
+-мезон образовался в результате слабого взаимодействия, и, следовательно, он должен был бы иметь h( 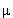 +) = +1. И если бы его масса, как и нейтрино, была бы равна нулю, распад
+) = +1. И если бы его масса, как и нейтрино, была бы равна нулю, распад 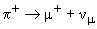 был бы запрещен. Но
был бы запрещен. Но 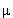 + имеет отличную от нуля массу. Поэтому он испускается в состоянии, которое является смесью состояний с "правильной" (h = +1) и "неправильной" (h = -1) спиральностями. Распад происходит благодаря примеси "неправильной" компоненты. Это позволяет объяснить подавление распада
+ имеет отличную от нуля массу. Поэтому он испускается в состоянии, которое является смесью состояний с "правильной" (h = +1) и "неправильной" (h = -1) спиральностями. Распад происходит благодаря примеси "неправильной" компоненты. Это позволяет объяснить подавление распада 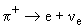 по сравнению с распадом
по сравнению с распадом 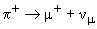 в 104 раз. В распаде
в 104 раз. В распаде 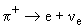 доля состояний с "неправильной" спиральностью гораздо меньше, чем в распаде
доля состояний с "неправильной" спиральностью гораздо меньше, чем в распаде 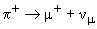 , так как me
, так как me 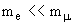 .
.
22. Показать, что зарядовые четности мезонов 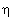 c(1S) и
c(1S) и 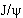 (1S) равны соответственно +1 и -1.
(1S) равны соответственно +1 и -1.
Зарядовая четность системы фермион-антифермион C = (-1)L(-1)J, где L - взаимный орбитальный момент, а J - полный момент (спин) системы. Мезоны 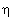 c(1S) и
c(1S) и 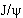 (1S) имеют одинаковый кварковый состав (c и
(1S) имеют одинаковый кварковый состав (c и 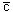 кварки) с нулевым орбитальным моментом (состояние 1S), но спин
кварки) с нулевым орбитальным моментом (состояние 1S), но спин 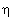 c(1S) равен 0, а спин
c(1S) равен 0, а спин 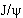 (1S) равен 1. Поэтому
(1S) равен 1. Поэтому 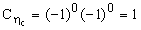 , а
, а 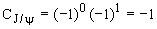 .
.
23. Как меняются при операции обращения времени следующие величины: импульс, момент количества движения, энергия, векторный и скалярный потенциалы, напряженность электрического и магнитного поля?
Импульс и момент количества движения меняют свои направления на противоположные так как эти величины по определению содержат производные по времени 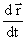 (импульс
(импульс 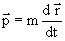 , момент количества движения
, момент количества движения 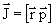 ).
).
При обращении времени энергия не меняется.
По определению
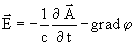
и
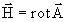 ,
,
где 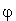 и
и 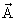 - скалярный и векторный потенциалы электромагнитного поля,
- скалярный и векторный потенциалы электромагнитного поля, 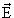 - напряженность электрического поля и
- напряженность электрического поля и 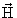 - напряженность магнитного поля. Уравнение движения заряда в электромагнитном поле будет
- напряженность магнитного поля. Уравнение движения заряда в электромагнитном поле будет
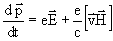 .
.
Уравнения движения инвариантны по отношению к обращению времени, поэтому вместе с заменой t на -t надо изменить знак магнитного поля, то есть уравнение движения не меняется, если провести замену
t  -t,
-t, 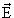

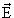 и
и 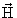
 -
- 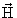 .
.
При этом скалярный потенциал не меняется, а векторный меняет знак:
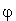

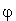 и
и 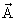
 -
- 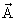 .
.
Таким образом, обращение времени оставляет скалярный потенциал и напряженность электрического поля неизменными, а векторный потенциал и напряженность магнитного поля при этом меняют направление на противоположное.
24. Показать, что спиральность частицы h инвариантна по отношению к обращению времени.
Спиральность частицы h по определению
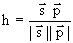 ,
,
где  - спин частицы, а
- спин частицы, а 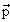 - ее импульс. При обращении времени как импульс, так и спин (момент количества движения) меняют знаки. Следовательно, спиральность, являющаяся произведением этих величин, должна сохраняться.
- ее импульс. При обращении времени как импульс, так и спин (момент количества движения) меняют знаки. Следовательно, спиральность, являющаяся произведением этих величин, должна сохраняться.
25.  +-мезон распадается в состоянии покоя. Нарисовать импульсы и спины частиц, образующихся в результате распада
+-мезон распадается в состоянии покоя. Нарисовать импульсы и спины частиц, образующихся в результате распада  +-мезона
+-мезона 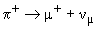 . Совершить C-, P-, CP-, T- и CPT-преобразования этого распада.
. Совершить C-, P-, CP-, T- и CPT-преобразования этого распада.
Импульсы и спины мюона и нейтрино в исходном распаде пиона будут выгдядеть следующим образом:
| (*) | 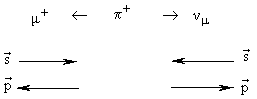 |
C-преобразование меняет знаки зарядов. Импульс и момент импульса остаются неизменными. В результате C-преобразования процесс (*) имеет вид
| C: | 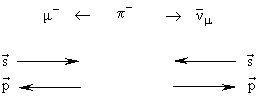 |
В результате C-преобразования получается ненаблюдаемый в природе процесс - образование мюонного антинейтрино с отрицательной спиральностью.
P-преобразование меняет направление импульса, направление момента импульса не меняется. В результате P-преобразования процесс (*) имеет вид
| P: | 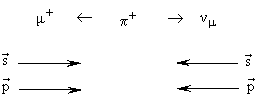 |
В результате P-преобразования получается ненаблюдаемый в природе процесс - образование мюонного нейтрино с положительной спиральностью.
CP-преобразование меняет знаки зарядов и направление импульса, момент импульса не меняется. В результате CP-преобразования процесс (*) имеет вид
| CP: | 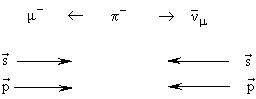 |
Комбинация двух последовательных преобразований C и P приводит к распаду с положительной спиральностью мюонного антинейтрино - процессу, наблюдаемому в природе.
В результате T-преобразования происходит изменение знаков импульса  , момента импульса
, момента импульса  и меняются местами начальное и конечное состояния
и меняются местами начальное и конечное состояния
 .
.
В результате T-преобразования процесс (*) имеет вид
| T: | 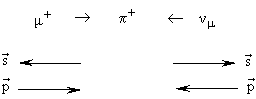 |
T-преобразование дает разрешенный распад.
CPT-преобразование меняет знаки зарядов, знак момента импульса, а также меняет местами начальное и конечное состояния. В результате CPT-преобразования процесс (*) имеет вид
| CPT: | 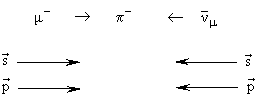 |
В силу CPT-инвариантности, если в природе происходит некоторый процесс, то точно с такой же амплитудой может происходить CPT-сопряженный процесс, в котором частицы заменены соответствующими античастицами, проекции их спинов и импульсов изменили знак, а начальное и конечное сосояния поменялись местами. На опыте не обнаружено ни одного случая нарушения CPT-инвариантности.
В результате CPT-преобразования получается процесс, который существует в природе.
26. Исходя из экспериментального значения угла Вайнберга sin2  W = 0.226 + 0.005 оценить величину слабого заряда gW и сравнить ее с величиной электрического заряда e.
W = 0.226 + 0.005 оценить величину слабого заряда gW и сравнить ее с величиной электрического заряда e.
Из единой теории электрослабых взаимодействий следует соотношение между электрическим и слабым зарядами: 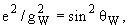 где e - элементарный электрический заряд, gW - слабый заряд,
где e - элементарный электрический заряд, gW - слабый заряд,  W - угол Вайнберга. Экспериментальное значение sin2
W - угол Вайнберга. Экспериментальное значение sin2  W = 0.226. Оценка отношения электрического заряда к слабому
W = 0.226. Оценка отношения электрического заряда к слабому 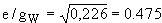 .
.
27. Возможен ли опыт по визуальному наблюдению промежуточных бозонов  , например, в пузырьковой, искровой, дрейфовой камере, ядерных фотоэмульсиях или другом трековом приборе?
, например, в пузырьковой, искровой, дрейфовой камере, ядерных фотоэмульсиях или другом трековом приборе?
Рассмотрим реакцию рождения  -бозонов
-бозонов 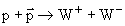 на крупнейшем протон-антипротоном коллайдере TEVATRON (Лаборатория им. Ферми, США) с энергией каждого пучка 1 ТэВ. Тогда W-бозоны будут рождаться с полной энергией Е = 1 ТэВ и от точки рождения до распада пройдут расстояние l =
на крупнейшем протон-антипротоном коллайдере TEVATRON (Лаборатория им. Ферми, США) с энергией каждого пучка 1 ТэВ. Тогда W-бозоны будут рождаться с полной энергией Е = 1 ТэВ и от точки рождения до распада пройдут расстояние l = 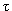 v, где
v, где 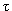 - время жизни W-бозона с учетом релятивистского замедления времени
- время жизни W-бозона с учетом релятивистского замедления времени
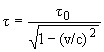
Среднее время жизни W-бозона в его собственной системе 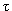 0
0 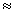
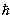 /Г , где Г - ширина распада W-бозона, равная 2.1 ГэВ. Отсюда
/Г , где Г - ширина распада W-бозона, равная 2.1 ГэВ. Отсюда
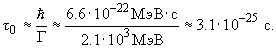
Из релятивистского соотношения для полной энергии
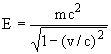
| находим скорость | 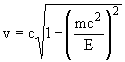 | и | 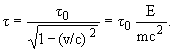 |
Отсюда имеем
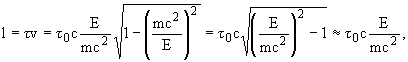
т.к. энергия покоя W-бозона (mc2 = 80 ГэВ) много меньше его полной энергии (E = 1 ТэВ).
l = 3.1 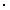 10-25 с x 3
10-25 с x 3 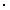 1010 см/с x (1000 МэВ/80 МэВ)
1010 см/с x (1000 МэВ/80 МэВ) 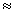 10-13 см
10-13 см 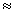 1 Фм.
1 Фм.
Таким образом, пробег промежуточного бозона до распада слишком мал (примерно в 10 раз меньше диаметра ядра), чтобы его можно было наблюдать в любом трековом приборе.
28. Определить длину L и время t пробега реакторного нейтрино в воде, воспользовавшись данными эксперимента Райнеса и Коуэна (1956 - 1959 г.г.), получившими для сечения взаимодействия антинейтрино с веществом 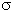
 10-43 см2.
10-43 см2.
Антинейтрино в реакторе рождается в реакции распада нейтрона
n  p + e- +
p + e- +  e.
e.
Число нейтрино прошедших через слой вещества толщиной х,
N(x) = N(0) exp(-n 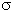 x),
x),
где n - количество ядер вещества в единице объема.
Определим L как длину, на которой поток антинейтрино уменьшается в е раз, то есть L = 1/ns . В свою очередь n = 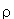 NA /A, где NA - число Авогадро,
NA /A, где NA - число Авогадро, 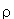 - плотность вещества, А - молярная масса. Для воды
- плотность вещества, А - молярная масса. Для воды 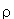 = 1 г/см3, А(Н2О) = 18. Откуда
= 1 г/см3, А(Н2О) = 18. Откуда
L = 1/ns = A/ 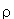 NA
NA 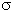 = 18/(1 г/см3 x 6
= 18/(1 г/см3 x 6 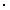 1023 x 10-43 см2) = 3
1023 x 10-43 см2) = 3 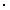 1020 см = 3
1020 см = 3 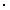 1015 км.
1015 км.
t = L /с = 3 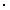 1015 км / 3
1015 км / 3 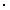 105 км/с = 1010 с
105 км/с = 1010 с 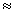 320 лет (1 год
320 лет (1 год 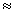 3.156
3.156 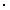 107 с).
107 с).
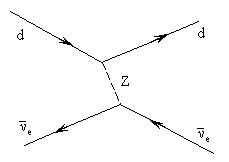
29. Нарисовать простейшие диаграммы Фейнмана взаимодействия реакторного антинейтрино с веществом.
Реакторное антинейтрино - электронное, то есть  e. Обычное вещество состоит из кварков первого поколения u, d и e-. Все возможные диаграммы взаимодействия
e. Обычное вещество состоит из кварков первого поколения u, d и e-. Все возможные диаграммы взаимодействия  e с этими частицами легко получить из диаграммы распада d-кварка, ответственного за распад нейтрона
e с этими частицами легко получить из диаграммы распада d-кварка, ответственного за распад нейтрона
d  u + e- +
u + e- +  e, n
e, n  p + e- +
p + e- +  e:
e:

Из этой диаграммы получаем диаграммы взаимодействия  e с u-кварком и электроном:
e с u-кварком и электроном:
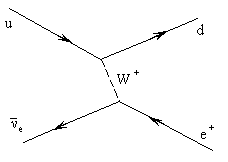 | 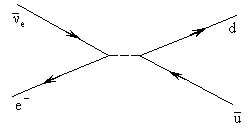 |
 e не будет взаимодействовать с d-кварком с участием W-бозона (нельзя нарисовать двухузловую диаграмму такого процесса). Однако
e не будет взаимодействовать с d-кварком с участием W-бозона (нельзя нарисовать двухузловую диаграмму такого процесса). Однако  e может рассеиваться на d-кварке, с участием Z-бозона.
e может рассеиваться на d-кварке, с участием Z-бозона.