Ишханов Б.С. Задачи с решениями. Свойства частиц и взаимодействий 4 страница

Рассмотрим теперь протон (u u d). Запишем (**) в виде

a(u u d) = a(uК uЗ dС) s(ru ru rd) (su su sd) (Iu Iu Id).

Переставим u-кварки. Изоспиновая функция к таким перестановкам симметрична. Значит должна быть симметрична и спиновая функция. Это означает, что спины u-кварков обязаны быть параллельными. Спин d-кварка антипараллелен спинам u-кварков, чтобы результирующий момент протона (его спин) был равен 1/2. Итак, (s_u s_u s_d) = ( 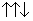). Эту ситуацию можно изобразить и так: 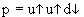. Аналогично рассуждая, можно получить , , .

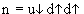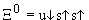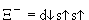36. Показать, что в супермультиплете легчайших барионов 1/2⁺ не может быть частиц, состоящих из кварков одинакового аромата u u u , d d d , s s s.

Рассмотрим комбинацию u u u. Пусть у зеленого и красного кварков спины параллельны:

_a(u u u) = _a(u_К u_З u_С) _s(r_u r_u r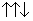_u) ( ) (I_u I_u I_u).

Изоспиновая функция симметрична к перестановке любой пары u-кварков. Поэтому симметричной обязана быть и спиновая функция. Однако, она антисимметрична к перестановке тех u-кварков, у которых спины антипараллельны. Таким образом, комбинация из трех одинаковых по аромату кварков в супермультиплете барионов 1/2⁺ ( l = 0) запрещена.

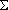37. Как направлены спины кварков в и ⁰?

Обе частицы имеют один и тот же кварковый состав u d s и входят в октет легчайших барионов с J^P = 1/2⁺. Рассмотрим . Ее изоспин равен нулю, то есть изоспиновая волновая функция антисимметрична к перестановке имеющих изоспин кварков u и d. Поэтому спиновая волновая функция так же обязана быть антисимметричной к перестановке u и d-кварков, откуда следует, что спины этих кварков в антипараллельны, а направление спина s-кварка произвольно, например .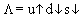

Рассмотрим ⁰. Это частица с изоспином 1, то есть ее изоспиновая волновая функция симметрична к перестановке несущих изоспин кварков u и d. Поэтому симметричной к такой перестановке будет и спиновая функция. Это означает, что спины u и d-кварка в ⁰ параллельны, а спин s-кварка направлен в противоположную сторону: .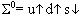

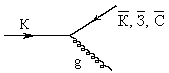38. 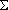⁰-гиперон распадается следующим образом: 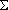⁰ + . Как меняются кварковые состояния при этом распаде? Определить тип и мультипольность испущенного фотона. Как направлен спин , если спин 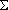⁰ направлен вверх?

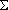⁰ и имеют одинаковый кварковый состав uds. Спины кварков в этих частицах направлены следующим образом: 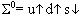, 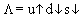. Отсюда следует, что при распаде ⁰ с излучением фотона "переворачивается" один из кварков (в данном примере d-кварк; направление его спина меняется на противоположное). Спин-четность ⁰ равны 1/2⁺. Таковы же и спин-четность . Откуда спин- четность излученного фотона 1⁺ , то есть излучается М1-фотон. Если до распада спин 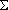⁰ был направлен вверх, то спин будет направлен вниз.

39. Показать, что кварк, испустив глюон, не может перейти в антикварк.

Пусть кварк имеет красный цвет. Тогда диаграмма предполагаемого условием задачи процесса имеет вид:

Поскольку имеет место закон сохранения цвета, то цветовая структура глюона g может быть получена из следующих равенств:

К = 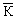+ g,
К = + g,
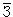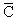К = + g,

откуда g = КК, КЗ или КС, что, очевидно, невозможно для глюона, поскольку последний должен иметь структуру цвет-антицвет.

40. Что можно сказать об электрическом квадрупольном моменте протона, нейтрона и других адронов?

В статической кварковой модели протон (нейтрон) состоят из трех кварков с нулевыми орбитальными моментами l = 0, то есть описываются сферически симметричными волновыми функциями. Поэтому электрические квадрупольные моменты протона и нейтрона должны быть равны нулю. Отличные от нуля электрические квадрупольные моменты могут быть у адронов, в которых кварки имеют l 0.

41. Одна из следующих двух диаграмм, описывающих распад n + ⁰ неправильна. Какая?

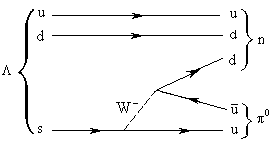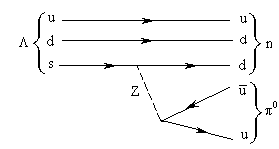Неправильная диаграмма справа. Z-бозон фигурирует в нейтральных слабых токах, не меняющих ароматы кварков, т.е. никаких связанных с кварками квантовых чисел. В правой диаграмме испускание Z-бозона сопровождается переходом s-кварка в d, при котором изменяется странность и изоспин.

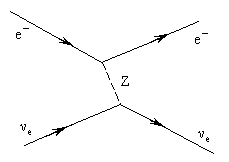
42. Возможно ли рассеяние нейтрино на электроне с участием 1) нейтрального слабого тока; 2) заряженного слабого тока? Положительный ответ сопроводить диаграммой процесса.

В нейтральных слабых токах переносчиком взаимодействия является Z-бозон, в заряженных слабых токах - 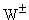. Оба вида рассеяния возможны и их диаграммы следующие:

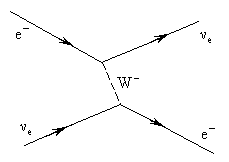43. Барионы ^- и ^- имеют близкие массы (соответственно 1197 и 1232 МэВ/с²) и распадаются одинаково:

^- n + ^-,
^- n + ^-.

За счет каких взаимодействий происходят эти распады? Нарисовать их кварковые диаграммы и оценить константу _w слабого взаимодействия, полагая константу сильного взаимодействия _s 1.

^- распадается за счет слабого, а ^-- за счет сильного взаимодействия. В первом случае не сохраняется странность и изоспин, а во втором все квантовые числа сохраняются.

Диаграммы распадов:

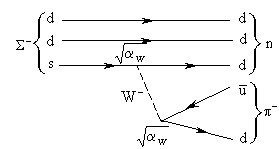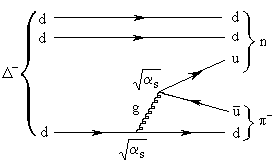Времена жизни ^- и ^- следующие: ( 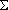^-) = 1.5 10^-10 с,

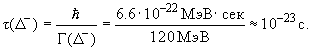
Время жизни t связано с константой распада в случае двухузловых диаграмм соотношением

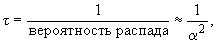
откуда

.

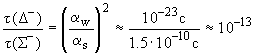Полагая _s 1, имеем _w 10^-6.

44. Одна из реакций ассоциированного рождения странных частиц ^- + p + K⁰ происходит за счет сильного взаимодействия, т.е. за время ~10^-23. Каждая из рожденных странных частиц и K⁰ распадается за счет слабых сил за время ~10^-10 сек. Из этих данных получите отношение констант слабого и сильного взаимодействий _w / _s.

Основными диаграммами рождения и распада странных частиц являются двухузловые диаграммы. Поэтому величина _w / _s может быть найдена из соотношения

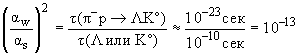
Откуда _w / _s 10^-6.

45. Почему отсутствие распада K^{+ +} + можно рассматривать как указание на нулевой спин K⁺–мезона?

Спин мезона ноль или целочислен. Если бы спин K⁺ был бы не равен нулю, например, 1, то из закона сохранения момента количества движения было бы (т.к. спин ⁺ равен нулю): 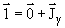и, поскольку четности K⁺ и ⁺ одинаковы, то возможно было бы излучение М1–фотона. При любом не равном нулю спине K⁺ можно было бы подобрать тип и мультипольность фотона, которые удовлетворяли бы законам сохранения момента и четности, и значит такой фотон должен был бы излучаться. Лишь в том случае, если спин K⁺ нулевой, излучение фотона запрещено, т.к. равенство 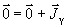для фотона невозможно поскольку его спин не может быть нулевым.

46. Определить относительный орбитальный момент p и ⁺, образующихся при распаде ⁺ p + ⁺.

Законы сохранения момента количества движения и четности для рассматриваемого распада имеют вид

( ⁺) = (p) + ( ⁺) + ,
.

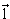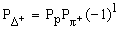Учитывая, что J( ⁺) = 3/2, J( p) = 1/2 и J( ⁺) = 0 из первого уравнения имеем l = 1 или 2. Т.к. внутренние четности участвующих частиц следующие: 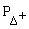= +1; P_p = +1 и 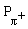= -1, то второе уравнение оставляет единственную возможность l = 1.

47. Захват отрицательных каонов в гелии иногда приводит к образованию гиперядер (ядер, в которых нейтрон заменен -гипероном) в соответствии с реакцией K^- + ⁴He 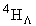+ ⁰. При изучении относительных мод распада 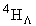и, в частности, из изотропии распадных продуктов установлено, что
J( 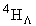) = 0. Покажите, что это означает отрицательную четность для K^-, независимо от углового момента состояния, из которого K^- был захвачен.

Если l – орбитальный угловой момент, а спины всех участвующих частиц равны нулю, то, перемножая четности в начальном и конечном состояниях, находим

(-1)^lP_K = (-1)l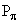

(внутренние четности ⁴He и 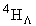положительны). Откуда P_K = 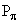= -1.

48. Покажите, что реакция p^- + d n + n + ⁰ не может идти для покоящихся пионов.

Т.к. J_d = 1 и рассматривается захват из s-состояния, в реакции будут участвовать состояния с J = 1 в начале и конце. Поскольку энерговыделение Q всего 0.5 МэВ, конечное состояние n и ⁰ должно быть s–состоянием. Следовательно, два нейтрона должны находиться в триплетном спиновом состоянии, что запрещено принципом Паули.

49. Ядро ³⁴Cl испытывает 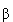⁺-распад: ³⁴Cl ³⁴S + e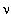⁺ + _e. Такой же тип 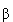-распада имеет место и для
⁺-мезона: ^{+ 0} + e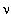⁺ + _e. Что еще сближает эти два 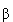⁺-распада? Оцените отношение вероятностей сравниваемых распадов и время жизни ⁺ относительно 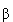⁺-распада, учитывая, что средние времена жизни ³⁴Cl и пиона собственно 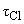= 1.5 с, 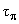= 2.6 10^-8 с и вероятность распада пиона по каналу e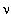⁺ _e около 10^-4.

Основные состояния ³⁴Cl и ³⁴S, также как ⁺ и ⁰, имеют нулевые спины. Поэтому оба 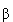-распада разрешенные фермиевского типа: 0⁺ 0⁺ и 0^- 0^- соответственно. Начальное и конечное ядро принадлежат к изоспиновому мультиплету с I = 1. То же самое относится и к пионам, участвующим в процессе. Кроме того, близки энерговыделения Q этих двух распадов (соответственно 5.0 и 4.1 МэВ). Вероятности распадов в единицу времен обратны средним временам жизни. Поэтому отношение вероятностей 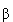⁺-распада ³⁴Cl и пиона с учетом того, что вероятность распада последнего по каналу e⁺ _e всего 10^-4, оказывается равной

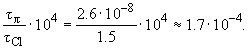
Время жизни ⁺ относительно ⁺-распада равно

10⁴ = 2.6 10^-8 с 10⁴ = 2.6 10^-4 с.

50. Среднее время жизни нейтрона 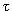_n = 890 с, а мюона 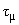= 2.2 10^-6 с. Покажите, что если принять во внимание разницу в энерговыделении (правило Сарджента), то константы взаимодействия в обеих случаях совпадают с точностью до фактора 10.

В распаде нейтрона энерговыделение 0.78 МэВ, а мюона - около 105 МэВ. Имеем для отношения констант распада _n/ 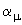с учетом правила Сарджента:

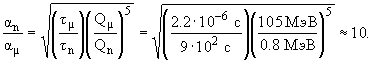
51. Среднее время жизни мюона равно 2.2 10^-6 с. Рассчитайте время жизни 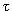-лептона, считая, что относительная вероятность распада 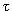⁺ e⁺ + _e + 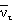составляет 18% и что 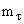c² = 1777 МэВ,
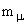c² = 105.7 МэВ. Сравните результат с измеренным временем жизни 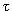-лептона 2.9 10^-13 с.

Используя правило Сарджента получаем для времени жизни 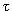-лептона

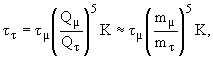
где K - относительная вероятность распада по каналу e⁺ n _e 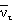, равная 0.18. Окончательно имеем

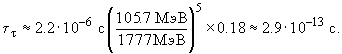
52. W-бозон распадается за счет слабого взаимодействия и время этого распада, оказывается

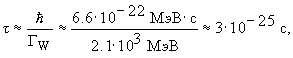
где G_W = 2.1 ГэВ - ширина распада W-бозона. Объяснить, почему это время столь мало и даже на два порядка ниже характерного времени распада за счет сильного взаимодействия.

Главная причина "сверхбыстрого" слабого распада W-бозона - большое энерговыделение Q_w m_wc² = 80 ГэВ. Согласно правилу Сарджента вероятность слабого распада зависит от энерговыделения в пятой степени. Оценим среднее время жизни W-бозона, исходя из времени распада -мезона 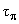= 2.6 10^-8 с. Энерговыделение при распаде -мезона ( ^{+ +} + )

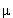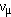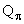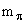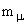= ( - ) c² = 140 МэВ - 106 МэВ = 34 МэВ.