Еоретична частина. Розділ 1.1, 1.3, 1.5, 1.6.
абораторна робота №7
 |
ВИЗНАЧЕННЯ МОМЕНТУ ІНЕРЦІЇ ТІЛА ДИНАМІЧНИМ МЕТОДОМ

Мета роботи
Визначити момент інерції тіла динамічним методом.
Прилади та обладнання
Вимірювальний пристрій, секундомір, штанґенциркуль, міліметрова лінійка.
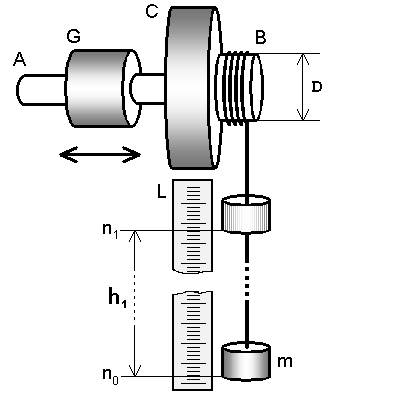 |
Опис вимірювального пристрою
|
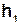 , то вантаж отримає запас потенціальної енерґії
, то вантаж отримає запас потенціальної енерґії 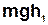 . Під дією сили тяжіння звільнений вантаж рівноприскорено опускається, при цьому система (вал з диском, шківом і маховиком) здійснює також рівноприскорений обертальний рух.
. Під дією сили тяжіння звільнений вантаж рівноприскорено опускається, при цьому система (вал з диском, шківом і маховиком) здійснює також рівноприскорений обертальний рух. Завдання 1. Знаходження моменту інерції системи, що
обертається
У процесі опускання вантажу масою m з висоти 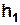 його потенціальна енерґія
його потенціальна енерґія 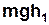 перетворюється у кінетичну енерґію поступального руху вантажу
перетворюється у кінетичну енерґію поступального руху вантажу 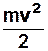 та кінетичну енерґію обертального руху системи
та кінетичну енерґію обертального руху системи 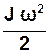 і частково втрачається на виконання роботи
і частково втрачається на виконання роботи 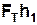 проти сил тертя
проти сил тертя 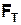 .
.
Згідно з законом збереження енерґії
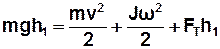 . . | (8) |
За інерцією система буде продовжувати обертатися і, внаслідок намотування нитки на шків, вантаж підніметься на висоту 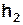
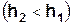 і на мить зупиниться. В цьому положенні він має потенціальну енерґію
і на мить зупиниться. В цьому положенні він має потенціальну енерґію 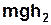 . Втрата потенціальної енерґії вантажу порівняно з початковим положенням дорівнює роботі проти сил тертя на шляху
. Втрата потенціальної енерґії вантажу порівняно з початковим положенням дорівнює роботі проти сил тертя на шляху 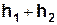 , тобто
, тобто
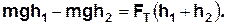 | (9) |
Звідси знаходимо силу тертя:
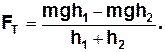 | (10) |
Оскільки вантаж опускається з висоти 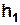 рівноприскорено без початкової швидкості, то у нижній точці траєкторії справедливі
рівноприскорено без початкової швидкості, то у нижній точці траєкторії справедливі
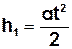 і v=αt, і v=αt, |
де t- час опускання тіла.
З цих рівнянь отримуємо кінцеву швидкість вантажу
v 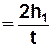 . . | (11) |
Швидкість вантажу рівна швидкості vточок на поверхні шківу і зв'язана з радіусом шківу R та його кутовою швидкістю 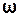 співвідношенням
співвідношенням
v 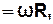 |
тому
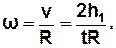 | (12) |
Підставивши значення 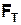 , v,
, v, 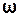 з формул (10), (11), (12) у формулу (8) та виразивши радіус шківа через його діаметр D після відповідних перетворень отримаємо для моменту інерції обертальної системи формулу:
з формул (10), (11), (12) у формулу (8) та виразивши радіус шківа через його діаметр D після відповідних перетворень отримаємо для моменту інерції обертальної системи формулу:
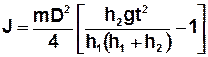 . . | (13) |
| G | Формула (13) спочатку використовується для експериментального визначення моменту інерції 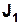 системи разом з додатковим диском, а потім, коли диск знято, - для вимірювання моменту інерції системи разом з додатковим диском, а потім, коли диск знято, - для вимірювання моменту інерції 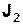 системи без додаткового диску. системи без додаткового диску. |
Завдання 2. Визначення моменту інерції додаткового
диска
Момент інерції додаткового диска можна визначити двома способами:
1) на основі результатів проведених експериментів, як різницю виміряних вище значень 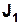 і
і 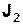 :
:
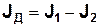 ; ; | (14) |
2) теоретично, виходячи з того, що додатковий диск є тілом правильної ґеометричної форми:
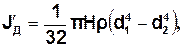 | (15) |
де H - товщина диску,
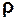 - густина матеріалу диску,
- густина матеріалу диску,
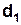 і
і  - зовнішній і внутрішній діаметри диску.
- зовнішній і внутрішній діаметри диску.
Вивести формули (15) самостійно одним із двох способів:
а) як моменту інерції тіла правильної ґеометричної форми
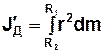 ; ; | (15.1) |
б) розглядаючи момент інерції додаткового диску як різницю моментів інерції великого диску радіуса R1, та вирізаного з нього малого диску радіуса R2 ( 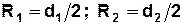 ). Скористатись тим, що момент інерції однорідного диску
). Скористатись тим, що момент інерції однорідного диску
 . . | (15.2) |
При підготовці до виконання роботи використати:
еоретична частина. Розділ 1.1, 1.3, 1.5, 1.6.
Послідовність виконання роботи
1. Закріпити диск G на валу А.
2. Опустити вантаж масою m, закріплений на нитці, у найнижче положення. Зафіксувати, напроти якої поділки 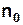 міліметрової шкали Lперебуває його основа.
міліметрової шкали Lперебуває його основа.
3. Намотуючи нитку на шків В, підняти вантаж у крайнє верхнє положення, зафіксувавши поділку 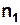 , як у п.2. Висота h1, на яку піднято вантаж, виразиться як:
, як у п.2. Висота h1, на яку піднято вантаж, виразиться як:
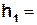 | | 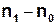 |. |. | (16) | |||
. Відпустити вантаж, увімкнувши одночасно секундомір. У момент, коли вантаж проходить нижнє положення, вимкнути секундомір і, продовжуючи спостерігати за підняттям вантажу, зафіксувати поділку 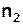 , до якої піднялася основа вантажу. Висота підняття: , до якої піднялася основа вантажу. Висота підняття:  | | 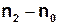 |. (17) 5. Записати час tопускання вантажу. Дослід повторити три рази, беручи в пункті 3 поділку |. (17) 5. Записати час tопускання вантажу. Дослід повторити три рази, беручи в пункті 3 поділку 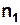 однаковою. Для обчислень однаковою. Для обчислень | ||||
використати середні значення часу t і висоти 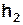 .
.
6. За допомогою штанґенциркуля виміряти діаметр шківу В в трьох різних напрямках і визначити середнє значення його діаметру D.
7. За формулою (13) обчислити момент інерції 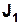 системи з диском.
системи з диском.
8. Зняти диск з валу.
9. Виконати всі операції, вказані в пунктах 3, 4. За формулою (13) обчислити момент інерції 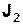 системи без диску.
системи без диску.
10. За формулою (14) обчислити момент інерції 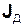 диску.
диску.
11. Виміряти товщину диску H, його зовнішній і внутрішній діаметри 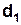 і
і  .
.
12. За формулою (15) обчислити момент інерції диску 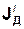 .
.
13. Порівняти одержані значення 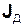 та
та 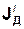 і за формулою (18) оцінити їх розбіжність.
і за формулою (18) оцінити їх розбіжність.
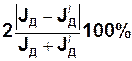 (18)
(18)
густина матеріалу диску 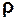 = 7,8·103 кг/м3
= 7,8·103 кг/м3
маса вантажу m=(250 ± 0,5)·10-3 кг
| G | При розрахунках моментів інерції перевести результати вимірювань всіх величин в одиниці СІ. |
Таблиці результатів вимірювань
1. При обертанні системи з диском
| № | h1, мм | Δh1, мм | t, с | Δt, с | h2, мм | Δh2, мм | D, мм | ΔD, мм |
| вимір | розрах. | вимір | розрах. | вимір | розрах. | вимір | розрах. | |
| вимір | розрах. | вимір | розрах. | вимір | розрах. | вимір | розрах. | |
| вимір | розрах. | вимір | розрах. | вимір | розрах. | вимір | розрах. | |
| сер. | розрах. | розрах. | розрах. | розрах. | розрах. | розрах. | розрах. | розрах. |
2. При обертанні системи без диску
| № | h1, мм | Δh1, мм | t, с | Δ t,с | h2, мм | Δh2, мм | D, мм | ΔD, мм |
| вимір | розрах. | вимір | розрах. | вимір | розрах. | вимір | розрах. | |
| вимір | розрах. | вимір | розрах. | вимір | розрах. | вимір | розрах. | |
| вимір | розрах. | вимір | розрах. | вимір | розрах. | вимір | розрах. | |
| сер. | розрах. | розрах. | розрах. | розрах. | розрах. | розрах. | розрах. | розрах. |
3. Ґеометричні розміри диску
| № | H, мм | ΔH, мм | d1, мм | Δd1, мм | d2, мм | Δd2, мм |
| вимір | розрах. | вимір | розрах. | вимір | розрах. | |
| вимір | розрах. | вимір | розрах. | вимір | розрах. | |
| вимір | розрах. | вимір | розрах. | вимір | розрах. | |
| сер. | розрах. | розрах. | розрах. | розрах. | розрах. | розрах. |
Контрольні запитання
1. Що називається моментом інерції тіла?
2. Що називається моментом сили відносно нерухомої осі обертання?
3. Пояснити основне рівняння динаміки обертального руху твердого
тіла відносно нерухомої осі.
4. Вивести формулу для моменту інерції однорідного диску відносно його ґеометриченої осі.
5. За якими формулами обчислюється кінетична енерґія поступального і обертального рухів тіла?
6. У чому полягає закон збереження і перетворення енерґії?
Рекомендована література
1. Курс фізики / За редакцією І.Є.Лопатинського.
– Львів: Вид. «Бескид Біт», 2002.
2. Трофимова Т.И. Курс физики.– М.: Высшая школа, 1990.
3. Савельев И. В. Курс общей физики, т.1 –М.: Наука, 1982.
