Ишханов Б.С. Задачи с решениями. Свойства частиц и взаимодействий 2 страница

| 2) |  | ||
| Q: | 1 - 1  1 - 1 1 - 1 |  Q = 0 Q = 0 | |
| B: | 1 - 1  - 1 + 1 - 1 + 1 |  B = 0 B = 0 | |
| S: | 0 + 0  3 - 3 3 - 3 |  S = 0 S = 0 | |
| I3: | 1/2 - 1/2  0 + 0 0 + 0 |  I3 = 0 I3 = 0 |
Законы сохранения выполнены.

| 3) |  | ||
| Q: | 1 + 0  - 1 + 1 + 1 - 1 + 1 + 1 |  Q = 0 Q = 0 | |
| B: | 0 + 1  1 + 0 + 0 1 + 0 + 0 |  B = 0 B = 0 | |
| S: | 0 + 0  - 2 + 1 + 1 - 2 + 1 + 1 |  S = 0 S = 0 | |
| I3: | 1 - 1/2  - 1/2 + 1/2 + 1/2 - 1/2 + 1/2 + 1/2 |  I3 = 0 I3 = 0 |
Законы сохранения выполнены.

11. Нарисовать основные диаграммы Фейнмана для следующих процессов: 1) рассеяние электрона на электроне; 2) эффект Комптона; 3) электрон-позитронная аннигиляция; 4) фотоэффект в кулоновском поле ядра; 5) образование электрон- позитронной пары в кулоновском поле ядра. Какие виртуальные частицы участвуют в этих процессах?
1) Рассеяние электрона на электроне. Виртуальная частица - фотон.

2) Эффект Комптона. Виртуальная частица - электрон.


3) Электрон-позитронная аннигиляция. Виртуальная частица - электрон или позитрон.


4) Фотоэффект в кулоновском поле ядра. Виртуальная частица - фотон.

5) Образование электрон-позитронной пары в кулоновском поле ядра. Виртуальная частица - фотон.


12. Оценить отношение сечений двух- и трехфотонной аннигиляции электрон-позитронной пары.
В квантовой электродинамике константа связи

Диаграмме с N узлами соответствует амплитуда процесса пропорциональная  Сечение процесса с N узлами пропорционально
Сечение процесса с N узлами пропорционально  .
.
В случае двухфотонной аннигиляции фейнмановская диаграмма имеет две вершины, поэтому сечение этого процесса можно оценить так -

В случае трехфотонной аннигиляции фейнмановская диаграмма имеет три вершины, и сечение этого процесса пропорционально

То есть отношение сечений


13. Какие из приведенных ниже слабых распадов адронов запрещены, а какие разрешены?
1)  ; 2)
; 2)  ; 3)
; 3)  .
.
Нарисовать диаграммы разрешенных распадов.
Лептонные слабые распады адронов с изменением странности подчиняются следующим правилам:
|  S| = 1 и
S| = 1 и  Q =
Q =  S, где
S, где  Q и
Q и  S - изменения электрического заряда и странности адронов.
S - изменения электрического заряда и странности адронов.
Определим изменения электрического заряда адронов Qадр и странности S в этих распадах:
| 1) |  | ||
| Qадр: | 0  - 1 - 1 |  Qадр = - 1 Qадр = - 1 | |
| S: | 1  0 0 |  S = - 1 S = - 1 |
Распад разрешен  Q =
Q =  S.
S.

| 2) |  | ||
| Qадр: | - 1  0 0 |  Qадр = 1 Qадр = 1 | |
| S: | - 1  0 0 |  S = 1 S = 1 |
Распад разрешен  Q =
Q =  S.
S.

| 3) |  | ||
| Qадр: | 0  - 1 - 1 |  Qадр = - 1 Qадр = - 1 | |
| S: | - 2  - 1 - 1 |  S = 1 S = 1 |
Распад запрещен  Q
Q 
 S.
S.
14. Нарисовать кварковые диаграммы распадов
1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  . Какие взаимодействия ответственны за эти распады?
. Какие взаимодействия ответственны за эти распады?
1)  |  |
Этот распад происходит в результате электромагнитного взаимодействия.
2)  |  |
Этот распад происходит в результате электромагнитного взаимодействия.
3)  |  |
Этот распад происходит в результате электромагнитного взаимодействия.
Разница в диаграммах распадов 2) и 3) связана с различием зарядовой четности  0-мезона
0-мезона  = +1 и
= +1 и  0- мезона
0- мезона  = - 1. Так как зарядовая четность
= - 1. Так как зарядовая четность  -кванта
-кванта  = -1, то распад
= -1, то распад  0- мезона возможен только при участии двух
0- мезона возможен только при участии двух  - квантов -
- квантов -  . Для
. Для  0 -мезона распад возможен с участием только одного
0 -мезона распад возможен с участием только одного  -кванта
-кванта  =
=  = -1.
= -1.
4)  |  |
Этот распад происходит в результате сильного взаимодействия.
15. Какие из перечисленных ниже четырех способов распада K+-мезона возможны? Для разрешенных нарисовать диаграммы, для запрещенных указать причину запрета.
1)  ; ; | 3)  ; ; |
2)  ; ; | 4)  ; ; |
Определим изменения электрического заряда Q, странности S и проекции изоспина I3 адронов и лептонного числа Le:
| 1) |  | ||
| Qадр: | 1  1 1 |  Qадр = 0 Qадр = 0 | |
| S: | 1  0 0 |  S = -1 S = -1 | |
| I3: | ½  1 1 |  I3 = 1/2 I3 = 1/2 | |
| Le: | 0  0 - 1 + 1 0 - 1 + 1 |  Le = 0 Le = 0 |
Распад запрещен, так как изменение странности адронов  S = -1, а изменение их электрического заряда
S = -1, а изменение их электрического заряда
 Qадр = 0, то есть
Qадр = 0, то есть  Q
Q 
 S.
S.
| 2) |  | ||
| Qадр: | 1  0 0 |  Qадр = -1 Qадр = -1 | |
| S: | 1  0 0 |  S = -1 S = -1 | |
| I3: | ½  0 0 |  I3 = -1/2 I3 = -1/2 | |
| Le: | 0  -1 + 1 -1 + 1 |  Le = 0 Le = 0 |
Распад разрешен - выполнены все законы сохранения для слабого взаимодействия. Слабое взаимодействие допускает несохранение странности и изоспина. Диаграмма этого распада:

| 3) |  | ||
| Qадр: | 1  0 0 |  Qадр = -1 Qадр = -1 | |
| S: | 1  0 0 |  S = -1 S = -1 | |
| I3: | ½  0 0 |  I3 = -1/2 I3 = -1/2 | |
| Le: | 0  0 - 1 - 1 0 - 1 - 1 |  Le = -2 Le = -2 |
Распад запрещен законом сохранения лептонного числа Le.
| 4) |  | ||
| Qадр: | 1  1 + 0 1 + 0 |  Qадр = -1 Qадр = -1 | |
| S: | 1  0 + 0 0 + 0 |  S = -1 S = -1 | |
| I3: | ½  1 + 0 1 + 0 |  I3 = 1/2 I3 = 1/2 |
Распад разрешен - выполнены все законы сохранения для слабого взаимодействия. Диаграмма этого распада:

16. Диаграммы показывают два варианта взаимодействия красного и зеленого кварков. Определить, за счет какого взаимодействия произошла реакция в каждом случае и что было виртуальной частицей.

В первом случае при взаимодействии двух кварков их цвет не изменяется. Это возможно, либр в сильном взаимодействии при обмене глюоном со скрытым цветом (К 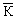 , З
, З 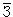 , С
, С 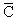 ), либо в электрослабом взаимодействии, когда виртуальными частицами являются не имеющие цвета фотон и Z-бозон. Наиболее вероятен вариант сильного взаимодействия с обменом глюоном, имеющим скрытый цвет.
), либо в электрослабом взаимодействии, когда виртуальными частицами являются не имеющие цвета фотон и Z-бозон. Наиболее вероятен вариант сильного взаимодействия с обменом глюоном, имеющим скрытый цвет.
Во втором случае цвет кварков изменился. Это возможно, только если взаимодействие между кварками сильное, и, следовательно, виртуальной частицей является глюон.
17. Показать, что пространственная четность позитрония (e+e- ) равна (-1)L+1, где L - относительный орбитальный момент e+ и e-.
Пространственная четность позитрония Pпоз определяется как произведение внутренней четности электрона и позитрона на орбитальный множитель (-1)L. Электрон и позитрон имеют значения спинов равные 1/2 и, следовательно, являются соответственно фермионом и антифермионом. Произведение внутренних четностей электрона и позитрона равна (-1), поскольку внутренняя четность фермиона противоположна внутренней четности антифермиона. Пространственная четность позитрония
Pпоз = (-1)(-1)L = (-1)L+1.
18. Какие значения может иметь относительный орбитальный момент двух  0-мезонов, образующихся в реакции
0-мезонов, образующихся в реакции  , если относительный орбитальный момент
, если относительный орбитальный момент  равен L?
равен L?
Относительный орбитальный момент двух  0-мезонов l определим из законов сохранения момента количества движения и четности. Получаем соотношение
0-мезонов l определим из законов сохранения момента количества движения и четности. Получаем соотношение

где  - внутренние четности протона, антипротона и
- внутренние четности протона, антипротона и  0-мезона. Внутренние четности протона
0-мезона. Внутренние четности протона  , антипротона
, антипротона  и
и  0-мезона
0-мезона  . Получаем, что (-1)(-1)L = (-1)l, то есть l = L + 1.
. Получаем, что (-1)(-1)L = (-1)l, то есть l = L + 1.
19. Как доказать несохранение четности в распаде  ?
?
Спиральность частицы есть
 ,
,
где  - спин частицы, а
- спин частицы, а  - ее импульс.
- ее импульс.
Состояние, при котором направления спина и импульса совпадают, соответствуют спиральности h = +1, а состояние с противоположно направленными спином и импульсом соответствует спиральности h = -1. Ультрарелятивистские фермионы, участвующие в любом слабом процессе, должны иметь значение спиральности h = -1 для частиц и h = +1 для античастиц.
Пион  + имеет спин, равный 0. При распаде
+ имеет спин, равный 0. При распаде  мюонное нейтрино как ультрарелятивистская частица будет обладать спиральностью h = -1. Соответственно, мюон, согласно законам сохранения импульса и момента импульса, также будет иметь спиральность равную h = -1. Хотя мюон и является античастицей, но в данном распаде его кинетическая энергия значительно меньше его массы покоя, так как
мюонное нейтрино как ультрарелятивистская частица будет обладать спиральностью h = -1. Соответственно, мюон, согласно законам сохранения импульса и момента импульса, также будет иметь спиральность равную h = -1. Хотя мюон и является античастицей, но в данном распаде его кинетическая энергия значительно меньше его массы покоя, так как  , и, следовательно, мюон нельзя считать релятивистским. Такой мюон может иметь спиральность h = -1.
, и, следовательно, мюон нельзя считать релятивистским. Такой мюон может иметь спиральность h = -1.

Применение к этому распаду операции пространственной инверсии приводит к тому, что нейтрино будет иметь спиральность h = +1, что невозможно для ультрарелятивистского фермиона. Отсутствие симметрии данного распада относительно пространственной инверсии указывает на несохранение пространственной четности в слабых взаимодействиях.
20. Возможен ли распад  0
0 
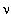 e +
e +  e для нейтрино с нулевой массой?
e для нейтрино с нулевой массой?
Нейтрино всегда имеет отрицательную спиральность, а антинейтрино всегда имеет положительную спиральность.
Спин нейтрино  равен 1/2, и направление его вектора противоположно направлению движения частицы. Спин антинейтрино
равен 1/2, и направление его вектора противоположно направлению движения частицы. Спин антинейтрино  также равен 1/2, но направление его вектора совпадает с направлением движения частицы.
также равен 1/2, но направление его вектора совпадает с направлением движения частицы.
При распаде, исходя из закона сохранения импульса, нейтрино должны разлетаться строго в противоположные стороны. Момент количества движения 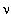 e и
e и  e
e  . Однако, спин
. Однако, спин  0-мезона равен 0, то есть данный распад невозможен из-за нарушения закона сохранения момента количества движения
0-мезона равен 0, то есть данный распад невозможен из-за нарушения закона сохранения момента количества движения 

21. Почему распад  сильно (в 104 раз) подавлен по сравнению с распадом
сильно (в 104 раз) подавлен по сравнению с распадом  хотя энерговыделение в распаде
хотя энерговыделение в распаде  во много раз больше, чем в распаде
во много раз больше, чем в распаде  ?
?
Ультрарелятивистские фермионы, участвующие в любом слабом процессе, должны иметь значение спиральности h = -1 для частиц и h = +1 для античастиц.
В указанных распадах нейтрино будут обладать спиральностью h = -1. Поэтому из закона сохранения момента импульса следует, что спин 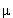 + должен быть направлен против его импульса.
+ должен быть направлен против его импульса. 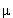 +-мезон образовался в результате слабого взаимодействия, и, следовательно, он должен был бы иметь h(
+-мезон образовался в результате слабого взаимодействия, и, следовательно, он должен был бы иметь h( 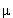 +) = +1. И если бы его масса, как и нейтрино, была бы равна нулю, распад
+) = +1. И если бы его масса, как и нейтрино, была бы равна нулю, распад  был бы запрещен. Но
был бы запрещен. Но 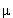 + имеет отличную от нуля массу. Поэтому он испускается в состоянии, которое является смесью состояний с "правильной" (h = +1) и "неправильной" (h = -1) спиральностями. Распад происходит благодаря примеси "неправильной" компоненты. Это позволяет объяснить подавление распада
+ имеет отличную от нуля массу. Поэтому он испускается в состоянии, которое является смесью состояний с "правильной" (h = +1) и "неправильной" (h = -1) спиральностями. Распад происходит благодаря примеси "неправильной" компоненты. Это позволяет объяснить подавление распада  по сравнению с распадом
по сравнению с распадом  в 104 раз. В распаде
в 104 раз. В распаде  доля состояний с "неправильной" спиральностью гораздо меньше, чем в распаде
доля состояний с "неправильной" спиральностью гораздо меньше, чем в распаде  , так как me
, так как me  .
.
