Ограничения на параметры системы

Описываемой классической физикой

Классическая физика применима, когда несущественны интерференция и дифракция частиц, приводящие к квантованию энергии и дискретности фазового пространства.

1. Высокие температуры, при которых несущественна дискретность спектра квантовых состояний:

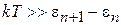, (П.1.5)

где 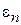– уровень энергии системы.

Для частицы в кубическом ящике со стороной L согласно (П.1.3)

.

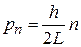Допустимые значения проекции импульса

,

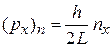и энергии частицы

.

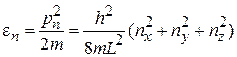Из (П.1.5) получаем

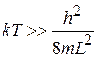. (П.1.6)

При большом размере системы и высокой температуре квантование энергии несущественно.

2. Большое расстояниеrмежду частицамипо сравнению с длиной волны де Бройля

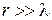. (П.1.7)

Согласно распределению Максвелла наиболее вероятная скорость частицы (2.45)

,

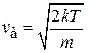тогда наиболее вероятный импульс

.

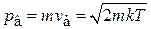Из (1.7)

.

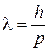получаем наиболее вероятную длину волны де Бройля частицы

.

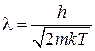Среднее расстояние 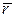между частицами газа выражаем через объем сосуда V и число частиц N

,

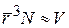откуда

,

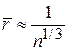где 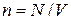– концентрация частиц. Условие (П.1.7) принимает вид

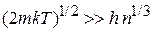. (П.1.8)

Классическая теория идеального газа выполняется при достаточно малых концентрациях, высоких температурах и не слишком малых массах частиц.

Сопоставляем (П.1.8) с химическим потенциалом (2.62а)

,

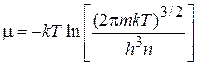получаем

m < 0.

В области применимости классической теории химический потенциал отрицателен.

Для гелия при нормальных условиях находим

,

,

,

,

,

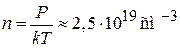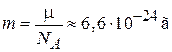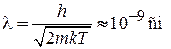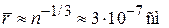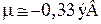выполняется 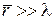и классическая физика применима.

Для электронов в металле при нормальной температуре

.

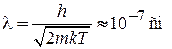Расстояние между узлами кристаллической решетки

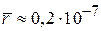см.

Условие 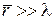нарушается. Классическая физика не применима для электронного газа в металле.

В полупроводниках длина волны де Бройля электрона при нормальной температуре и ширина запрещенной зоны

Т = 300 К	Ge	Si	GaAs	InSb
λ, мкм	6×10–3	7,7×10–3	2,9×10–2	6,7×10–2
Eg, эВ	0,67	1,12	1,42	0,17

В узкозонных полупроводниках с шириной запрещенной зоны 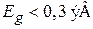, например InSb, InAs, концентрация электронов проводимости велика, расстояние r между электронами достигает микронных размеров, условие классического описания 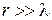нарушается.

Большой объем фазового пространства, приходящийся на частицу, по сравнению с постоянной Планка

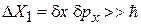. (П.1.9)

Выразим флуктуации через параметры системы. По теореме о распределении энергии по степеням свободы средняя кинетическая энергия одномерного движения узла кристаллической решетки

,

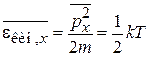тогда

.

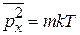Тепловая флуктуация проекции импульса с учетом 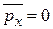равна

.

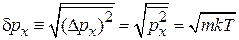Средняя потенциальная энергия упругих колебаний по теореме о распределении энергии по степеням свободы

,

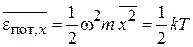тогда

.

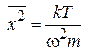где w – круговая частота собственных колебаний узлов кристалла. Чем прочнее кристалл, тем больше частота:

медь – ,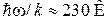

алмаз – .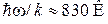

Тепловая флуктуация координаты узла с учетом 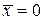равна

.

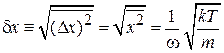В результате

.

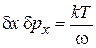Условие (П.1.9) получает вид

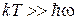. (П.1.10)

Чем прочнее кристалл и ниже температура, тем меньше согласие с классической теорией. Классическая физика не применима для прочных кристаллов при низкой температуре.

Для систем, нарушающих хотя бы одно из полученных условий, необходимо использовать квантовую статистическую физику.

Вопросы коллоквиума

1. Фазовое пространство для идеального газа. Микросостояние и макросостояние. Фазовый ансамбль. Число степеней свободы. Число микросостояний. Плотность микросостояний фазового ансамбля. Теорема Лиувилля.

2. Каноническое распределение. Условие применимости. Статистический интеграл. Свободная энергия. Применение к идеальному газу. Статистический интеграл поступательного движения частицы.

3. Распределение энергии частицы по степеням свободы для гамильтониана со степенными зависимостями. Неустранимая погрешность измерительного прибора с упругой силой.

4. Распределение Максвелла по модулю скорости и по энергии для концентрации частиц. Наиболее вероятные и средние значения.

5. Распределение Больцмана по координатам для концентрации частиц. Формула Больцмана для однородного поля тяжести.

6. Термодинамические потенциалы. Внутренняя энергия. Химический и электрохимический потенциал. Условие равновесия системы. Химический потенциал и статистический интеграл. Зависимости химического потенциала.

Вопросы экзамена

1. Биномиальное распределение. Дробовой шум.

2. Статистическое описание системы частиц в фазовом пространстве. Функция распределения. Теорема Лиувилля.

3. Микроканоническое распределение. Энергетическая плотность состояний. Термодинамические величины. Вычисление плотности состояний идеального газа.

4. Каноническое распределение. Статистический интеграл. Термодинамические величины. Вычисление статистического интеграла поступательного движения.

5. Распределение энергии по степеням свободы. Неустранимая погрешность измерительного прибора. Закон Дюлонга и Пти.

6. Распределение энергии по степеням свободы. Флуктуационная ЭДС в активном сопротивлении.

7. Распределение Максвелла по скорости и по энергии. Средние значения скоростей и энергии.

8. Плотность потока частиц, плотность потока энергии.

9. Термоэлектронная эмиссия. Формула Ричардсона.

10. Распределение Больцмана. Газ в центрифуге.

11. Распределение Больцмана. Поляризация диэлектрика.

12. Термодинамические характеристики системы с переменным числом частиц. Химический потенциал и его вычисление для идеального газа.

13. Распределение Максвелла–Больцмана по состояниям.

14. Большое каноническое распределение. Выражения для термодинамических характеристик.