Ишханов Б.С. Задачи с решениями. Свойства частиц и взаимодействий 3 страница

22. Показать, что зарядовые четности мезонов _c(1S) и (1S) равны соответственно +1 и -1.

Зарядовая четность системы фермион-антифермион C = (-1)^L(-1)^J, где L - взаимный орбитальный момент, а J - полный момент (спин) системы. Мезоны _c(1S) и (1S) имеют одинаковый кварковый состав (c и кварки) с нулевым орбитальным моментом (состояние 1S), но спин _c(1S) равен 0, а спин (1S) равен 1. Поэтому , а .

23. Как меняются при операции обращения времени следующие величины: импульс, момент количества движения, энергия, векторный и скалярный потенциалы, напряженность электрического и магнитного поля?

Импульс и момент количества движения меняют свои направления на противоположные так как эти величины по определению содержат производные по времени (импульс , момент количества движения ).
При обращении времени энергия не меняется.
По определению

и

,

где и - скалярный и векторный потенциалы электромагнитного поля, - напряженность электрического поля и - напряженность магнитного поля. Уравнение движения заряда в электромагнитном поле будет

.

Уравнения движения инвариантны по отношению к обращению времени, поэтому вместе с заменой t на -t надо изменить знак магнитного поля, то есть уравнение движения не меняется, если провести замену

t -t, и - .

При этом скалярный потенциал не меняется, а векторный меняет знак:

и - .

Таким образом, обращение времени оставляет скалярный потенциал и напряженность электрического поля неизменными, а векторный потенциал и напряженность магнитного поля при этом меняют направление на противоположное.

24. Показать, что спиральность частицы h инвариантна по отношению к обращению времени.

Спиральность частицы h по определению

,

где - спин частицы, а - ее импульс. При обращении времени как импульс, так и спин (момент количества движения) меняют знаки. Следовательно, спиральность, являющаяся произведением этих величин, должна сохраняться.

25. ⁺-мезон распадается в состоянии покоя. Нарисовать импульсы и спины частиц, образующихся в результате распада ⁺-мезона . Совершить C-, P-, CP-, T- и CPT-преобразования этого распада.

Импульсы и спины мюона и нейтрино в исходном распаде пиона будут выгдядеть следующим образом:

(*)

C-преобразование меняет знаки зарядов. Импульс и момент импульса остаются неизменными. В результате C-преобразования процесс (*) имеет вид

C:

В результате C-преобразования получается ненаблюдаемый в природе процесс - образование мюонного антинейтрино с отрицательной спиральностью.
P-преобразование меняет направление импульса, направление момента импульса не меняется. В результате P-преобразования процесс (*) имеет вид

P:

В результате P-преобразования получается ненаблюдаемый в природе процесс - образование мюонного нейтрино с положительной спиральностью.
CP-преобразование меняет знаки зарядов и направление импульса, момент импульса не меняется. В результате CP-преобразования процесс (*) имеет вид

CP:

Комбинация двух последовательных преобразований C и P приводит к распаду с положительной спиральностью мюонного антинейтрино - процессу, наблюдаемому в природе.
В результате T-преобразования происходит изменение знаков импульса , момента импульса и меняются местами начальное и конечное состояния

.

В результате T-преобразования процесс (*) имеет вид

T:

T-преобразование дает разрешенный распад.
CPT-преобразование меняет знаки зарядов, знак момента импульса, а также меняет местами начальное и конечное состояния. В результате CPT-преобразования процесс (*) имеет вид

CPT:

В силу CPT-инвариантности, если в природе происходит некоторый процесс, то точно с такой же амплитудой может происходить CPT-сопряженный процесс, в котором частицы заменены соответствующими античастицами, проекции их спинов и импульсов изменили знак, а начальное и конечное сосояния поменялись местами. На опыте не обнаружено ни одного случая нарушения CPT-инвариантности.
В результате CPT-преобразования получается процесс, который существует в природе.

26. Исходя из экспериментального значения угла Вайнберга sin² _W = 0.226 + 0.005 оценить величину слабого заряда g_W и сравнить ее с величиной электрического заряда e.

Из единой теории электрослабых взаимодействий следует соотношение между электрическим и слабым зарядами: где e - элементарный электрический заряд, g_W - слабый заряд, _W - угол Вайнберга. Экспериментальное значение sin² _W = 0.226. Оценка отношения электрического заряда к слабому .

27. Возможен ли опыт по визуальному наблюдению промежуточных бозонов 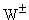, например, в пузырьковой, искровой, дрейфовой камере, ядерных фотоэмульсиях или другом трековом приборе?

Рассмотрим реакцию рождения 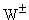-бозонов на крупнейшем протон-антипротоном коллайдере TEVATRON (Лаборатория им. Ферми, США) с энергией каждого пучка 1 ТэВ. Тогда W-бозоны будут рождаться с полной энергией Е = 1 ТэВ и от точки рождения до распада пройдут расстояние l = 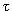v, где 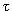- время жизни W-бозона с учетом релятивистского замедления времени

Среднее время жизни W-бозона в его собственной системе 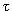₀ /Г , где Г - ширина распада W-бозона, равная 2.1 ГэВ. Отсюда

Из релятивистского соотношения для полной энергии

находим скорость

и

Отсюда имеем

т.к. энергия покоя W-бозона (mc² = 80 ГэВ) много меньше его полной энергии (E = 1 ТэВ).

l = 3.1 10^-25 с ^x 3 10¹⁰ см/с ^x (1000 МэВ/80 МэВ) 10^-13 см 1 Фм.

Таким образом, пробег промежуточного бозона до распада слишком мал (примерно в 10 раз меньше диаметра ядра), чтобы его можно было наблюдать в любом трековом приборе.

28. Определить длину L и время t пробега реакторного нейтрино в воде, воспользовавшись данными эксперимента Райнеса и Коуэна (1956 - 1959 г.г.), получившими для сечения взаимодействия антинейтрино с веществом 10^-43 см².

Антинейтрино в реакторе рождается в реакции распада нейтрона

n p + e^- + _e.

Число нейтрино прошедших через слой вещества толщиной х,

N(x) = N(0) exp(-n x),

где n - количество ядер вещества в единице объема.

Определим L как длину, на которой поток антинейтрино уменьшается в е раз, то есть L = 1/ns . В свою очередь n = N_A /A, где N_A - число Авогадро, - плотность вещества, А - молярная масса. Для воды = 1 г/см³, А(Н₂О) = 18. Откуда

L = 1/ns = A/ N_A = 18/(1 г/см^{3 x} 6 10^{23 x} 10^-43 см²) = 3 10²⁰ см = 3 10¹⁵ км.
t = L /с = 3 10¹⁵ км / 3 10⁵ км/с = 10¹⁰ с 320 лет (1 год 3.156 10⁷ с).

29. Нарисовать простейшие диаграммы Фейнмана взаимодействия реакторного антинейтрино с веществом.

Реакторное антинейтрино - электронное, то есть _e. Обычное вещество состоит из кварков первого поколения u, d и e^-. Все возможные диаграммы взаимодействия _e с этими частицами легко получить из диаграммы распада d-кварка, ответственного за распад нейтрона

d u + e^- + _e, n p + e^- + _e:

Из этой диаграммы получаем диаграммы взаимодействия _e с u-кварком и электроном:

_e не будет взаимодействовать с d-кварком с участием W-бозона (нельзя нарисовать двухузловую диаграмму такого процесса). Однако _e может рассеиваться на d-кварке, с участием Z-бозона.

Аналогичный вид имеют диаграммы рассеивания _e на u-кварке и электроне.

30. Из характеристик переносчиков слабого взаимодействия 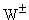и Z бозонов определить радиус слабых сил.

Массы W и Z бозонов: m_W 80 ГэВ/c², m_Z 90 ГэВ/c². Радиус действия слабых сил a_W связан с массой переносчиков взаимодействия W и Z бозонов соотношением:

(*),

следующими из соотношения неопределенности E t . Действительно, нарушение закона сохранения энергии на величину E = m_W c² m_Z c² ненаблюдаемы в течение временных интервалов

t< / E /m_W c² /m_Z c².

Откуда следует (*). Так как m_W m_Z 100 ГэВ/c², имеем

a_W 0.2 ГэВ Фм/100 ГэВ = 2 10^-3 Фм.

31. Протон, поглощая фотон, переходит в ⁺. Определить тип, мультипольность и энергию фотона.

Протон р и ⁺ имеют массы
m_p = 938,3 МэВ/c², = 1232 МэВ/c² и спины-четности J^P(p) = 1/2⁺, J^P( ⁺) = 3/2⁺. Характеристики фотона получаются из законов сохранения полного момента количества движения и четности (процесс электромагнитный):

;

или

;

Откуда J = 1 или 2, а = +1. Поэтому, рассматриваемый в задаче процесс осуществляется М1 и Е2-фотонами. Энергия фотона

= c² - m_pc² = (1232 - 938) МэВ 300 МэВ.

32. Какая энергия нужна для "переворота" кварка в нуклоне?

Рассмотрим протон р и ⁺. Обе частицы имеют одинаковый кварковый состав u u d и нулевой результирующий орбитальный момент кварков. Но у протона спин d-кварка противоположен спину u-кварков, а у ⁺ спины всех кварков направлены в одну сторону: p 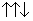= u u d ( ), ⁺ = u u d ( ). Таким образом от протона к ⁺ можно перейти, изменив направление спина d-кварка, то есть "перевернув" его. Для перехода протона в ⁺ требуется энергия около 300 МэВ, то есть для "переворота" кварка в протоне нужна энергия около 300 МэВ.

33. Определить магнитные моменты u и d-кварков в ядерных магнетонах, считая, что их масса равна 1/3 массы нуклона.

Всякая точечная заряженная частица со спином 1/2, массой m и зарядом q имеет величину собственного магнитного момента

.

Исходя из этого, для u и d-кварка соответственно имеем:

где - ядерный магнетон.

34. Могут ли топ-кварк ( t ) и его антикварк ( ) образовать связанную систему t - топоний, аналогичную чармонию (с ) и ботомонию (b )?

О связанной системе кварков можно говорить лишь в том случае, когда она существует в течение времени большем, чем требуется частице со скоростью света для преодоления расстояния 1 Фм (размер адрона), то есть

10^-13 см / 3 10¹⁰ см/с 10^-23 10^-24 сек.

Топ-кварк имеет ширину распада Г_t 2 ГэВ, откуда время жизни топ-кварка

t _t /Г 6.6 10^-22 МэВ с / 2 10³ МэВ = 3,3 10^-25 сек,

то есть слишком мало, чтобы он успел образовать связанную систему t .

35. Показать, что для частиц октета легчайших барионов с J^P = 1/2⁺ выполняется следующее правило: у кварков одинакового аромата спины параллельны.

Волновая функция бариона (системы из трех кварков) может быть записана в следующем виде

(1,2,3) = (К З С) (r1 r2 r3) (s1 s2 s3) (I1 I2 I3)

(*)

где 1, 2, 3 - совокупность всех координат и квантовых чисел кварков, а произведение четырех функций справа - это произведение соответственно цветовой (К - красный, З - зеленый, С - синий), пространственной, спиновой и изоспиновой частей волновой функции бариона. (1, 2, 3) должна быть антисимметрична в целом к перестановке всех квантовых чисел и координат двух тождественных кварков (кварки u и d остаются тождественными, поскольку составляют изоспиновой дублет). При этом цветовая, пространственная, спиновая и изоспиновая функции в отдельности могут быть как симметричными (s), так и антисимметричными (a). (К З С) всегда антисимметрична, так как кварки в барионе разноцветны. Для легчайших барионов орбитальные моменты кварков l = 0 и пространственная функция (r₁ r₂ r₃) - симметрична. В этом случае (*) переписывается в виде

a(1, 2, 3) = a(К З С) s(r1 r2 r3) (s1 s2 s3) (I1 I2 I3)

(**)

Отсюда следует, что в супермультиплетах легчайших барионов (например, октете J^P = 1/2⁺ и декуплете J^P = 3/2⁺) допустимы лишь такие кварковые комбинации, у которых спиновая и изоспиновая функции одновременно либо симметричны, либо антисимметричны, то есть спиново-изоспиновая функция либо
_s(s₁ s₂ s₃) _s(I₁ I₂ I₃), либо _a(s₁ s₂ s₃) _a(I₁ I₂ I₃).