Соотношения неопределенностей

Из (1.4), (1.7) и (1.5), (1.6)

,

,

,

,

,

,

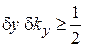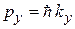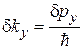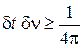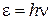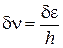получаем соотношения неопределенностей для флуктуаций

,

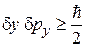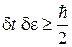. (1.9)

Чем точнее измеряется координата кванта, тем неопределеннее соответствующая проекция импульса; чем меньше длительность излучения фотона, тем больше неопределенность его энергии.

Энергия N квантов, связанных с волной частотой ω, равна 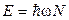. Фаза волны линейно зависит от времени 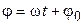. Неопределенности энергии и фазы

, .

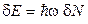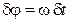С учетом (1.9)

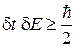
получаем

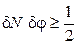. (1.9а)

Чем точнее измеряется фаза волны, тем неопределеннее число квантов, связанных с волной; чем точнее измеряется число квантов, темнеопределеннее фаза волны. В результате для одного кванта не существует определенной фазы волны.

В двух волнах измеримы одновременно и с неограниченной точностью:

Или суммарное число фотонов и разность фаз волн,

или сумма фаз волн и разность чисел фотонов.

Если на преграду с двумя щелями падает волна с определенным числом квантов, то фаза этой волны не имеет определенного значения. Волны, прошедшие щели, накладываются друг на друга. На экране образуется интерференционная картина, зависящая от разности фаз складывающихся волн. Невозможно найти число квантов, прошедших через каждую из щелей, без нарушения интерференционной картины. Чем точнее измеряется число квантов, прошедших через одну из двух щелей, тем неопределеннее разность фаз прошедших волн и сильнее размывается интерференционная картина.

Эксперименты с отдельными квантами показывают, что по пути к экрану квант проходит через обе щели.

Средняя концентрация фотонов

Энергия единицы объема согласно (1.2)

,

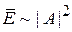Энергия одного фотона (1.6)

,

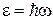тогда средняя концентрация фотонов

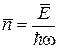
пропорциональна квадрату модуля волны

.

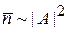Если волна содержит один фотон, то вместо концентрации используется вероятность обнаружения фотона в единице объема, или плотность вероятности. В результате плотность вероятности пропорциональна квадрату модуля волны

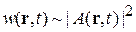. (1.10)

Волна де Бройля

Луи де Бройль в 1924 г. предположил, что корпускулярно-волновая двойственность присуща не только свету, но и частицам вещества. Результаты для фотона переносим на частицу.

Фотон связан с волной (1.8)

.

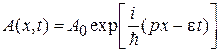Частице массой m, движущейся вдоль оси x в поле с потенциальной энергией 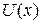и с полной энергией Е сопоставляем волну де Бройля, или волновую функцию:

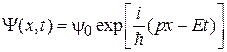, (1.11)

где

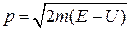– импульс частицы,

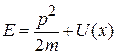– полная энергия.

Из (1.7) получаем длину волны де Бройля

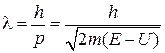. (1.13)