Розділ 2. Принципи спеціальної теорії відносності. 3 страница

Зробимо кілька загальних зауважень про рівняння (5.1) – (5.4)

Зауваження 1. Диференціальні рівняння (5.1) – (5.4) з математичної точки зору представляють з себе систему лінійних диференціальних рівнянь у частинних похідних 1-го порядку, що зв'язує характеристики зарядів

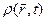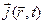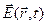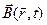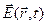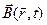( , ), що рухаються у вакуумі, і електромагнітного поля ( , ). Лінійність рівнянь (5.1) – (5.4) зв'язана з фізичним принципом суперпозиції електромагнітних полів; дійсно, якщо і є розв’язком цієї системи, то внаслідок лінійності рівнянь розв’язком будуть і суперпозиції 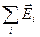й 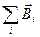у чому легко переконатися.

Зауваження 2. Загальні розв’язки рівнянь (5.1) – (5.4) будуть містити довільні постійні. Для одержання ж часткових розв’язків (за допомогою яких тільки і можна описати визначену фізичну ситуацію) необхідно додатково задати граничні і початкові умови, що відповідають конкретній постановці задачі в області електродинаміки (наприклад, вирішити задачу Коші), що дає можливість визначити невідомі постійні.

Зауваження 3. Обмеження на застосовність законів електродинаміки (5.1) і (5.4) накладають загальна теорія відносності і фундаментальні теорії квантово-польової картини світу (див. про це ч. I, вступ). Можна вважати, що в більшості фізичних ситуацій (крім фізики "чорних дір", де гравітаційні поля дуже сильні) гравітаційне поле слабко взаємодіє з електромагнітним, тому в переважній більшості випадків можна зневажити обмеженнями, що накладаються на електродинаміку ЗТВ. Основні обмеження на електродинаміку вакууму накладає КМ і КТМ, що і встановлюють основні границі застосовності рівняння (5.1) – (5.4). Аналіз показує, в електромагнітних полях досить високої інтенсивності і великої частоти (ці ситуації реалізуються, наприклад, усередині атомів) істотного значення набувають квантові властивості електромагнітного поля, що коректно описуються квантовою електродинамікою (див. ч. III). Поза атомними масштабами рівняння (5.1) – (5.4) залишаються надійною основою опису електромагнітних явищ.

§6. Електромагнітні потенціали.

При записі рівнянь електродинаміки вакууму (5.1) – (5.4) у §5 були використані характеристики електромагнітного поля 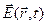і 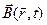що мають безпосередній фізичний зміст, тобто експериментально вимірні. У принципі цих характеристик цілком достатньо для рішення будь-якої електродинамічної задачі у вакуумі. Однак рішення багатьох питань електродинаміки (наприклад, у теорії випромінювання електромагнітних хвиль) значно спрощується, якщо ввести в розгляд нові, допоміжні характеристики електромагнітного поля – так названі електромагнітні потенціали, основна перевага яких полягає в тому, що вони підкоряються диференціальним рівнянням другого порядку, для яких розроблені потужні математичні методи їхнього інтегрування.

Нові характеристики електромагнітного поля зручно ввести на основі рівнянь Максвела (5.1) – (5.4). Оскільки div rot º 0, то рівняння (5.4) автоматично задовольняється, якщо замість магнітної індукції 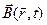ввести інше векторне поле 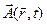, визначивши його співвідношенням:

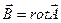. (6.1)

Векторне поле 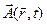називається векторним потенціалом електромагнітного поля.Підставляючи (6.1) у (5.2), приводимо останнє до вигляду:

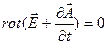
З урахуванням тотожності rot grad º 0, це рівняння автоматично задовольняється, якщо покласти:

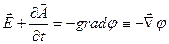
(знак "-" принципового значення не має; ми його записали, випливаючи історичним традиціям викладу електродинаміки), тобто якщо визначити скалярну функцію 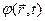співвідношенням

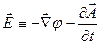(6.2)

Скалярне поле 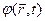називається скалярним потенціалом електромагнітного поля.

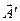Співвідношення (6.1) – (6.2) визначають електромагнітні потенціали неоднозначно. Дійсно, якщо від потенціалів і перейти до інших потенціалів і 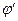за допомогою перетворень:

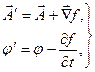(6.3)

де 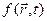- довільна функція, то електромагнітне поле не змінюється:

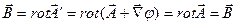
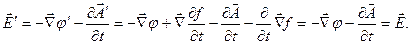
Перетворення (6.3) називається каліброваним перетворенням, а інваріантість електромагнітних полів щодо цих перетворень називається каліброваною інваріантістю. Неоднозначністю (6.3) потенціалів можна скористатися, щоб довизначити (калібрувати) їх, наклавши на них деяку додаткову (калібровану) умову. Найчастіше на потенціали накладають додаткову (калібровану) умову:

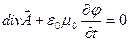, (6.4)

яке називається каліброваною умовою Лоренца чи просто калібруванням Лоренца. Покажемо, що завдяки неоднозначності вибору потенціалів для довільного електромагнітного поля їх завжди можна вибрати так, щоб вони задовольняли умові Лоренца. Допустимо, що ми знайшли потенціали і , що описують досліджуване електромагнітне поле, але не задовольняють умові (6.4). 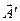Підберемо таку функцію f, щоб нові потенціали і 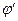цій умові задовольняли, тобто зажадаємо, щоб виконувалася умова:

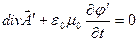
Підставляючи сюди (6.3), знаходимо, рівняння для шуканої функції f:

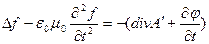, (6.5)

де D º div grad - оператор Лапласа. Але рівняння (6.5) має вигляд рівняння Д’аламбера і, як відомо, завжди має розв’язок. Таким чином, завжди можна підібрати таку f, щоб електромагнітні потенціали задовольняли умові калібрування Лоренца, тому надалі, якщо не обговорене зворотне, ми завжди будемо вважати, що умова (6.4) виконується.

Зауваження 1. Виявляється, що навіть при виконанні умови Лоренца (6.4) потенціали ще не визначаються однозначно. Справді, якщо взяти таку функцію f, що задовольняє хвильовому рівнянню:

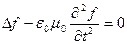(6.6)

то перетворення (6.3) призведуть до нових потенціалів 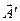і 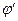, які, як це випливає з (6.5), задовольняють умові (6.4) одночасно з потенціалами і .

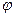Зауваження 2. Електромагнітні потенціали являють приклад, як говорять, величин що не спостерігаються, які часто й істотно використовуються в аналітичному апараті сучасної теоретичної фізики (ще одним прикладом таких величин є хвильова функція в КМ).

Неспостерегливість (незмірність мовою експериментальної фізики) потенціалів зв'язана з їхньою неоднозначністю. Відзначимо тут, що популярні серед деяких фізиків-теоретиків методологічні установки, спрямовані на виключення з фізичних теорій величин, що не спостерігаються, і прагнення використовувати величин, що тільки спостерігаються, виявилися безперспективними: сучасна теоретична фізика не може успішно розвиватися без використання величин, що не спостерігаються.

Одержимо тепер рівняння для електромагнітних потенціалів. Для цього підставимо (6.1) і (6.2) у ще не використані нами рівняння 1 і 3 і після нескладних перетворень одержимо:

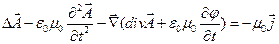(6.7)

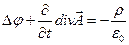(6.8)

З урахуванням калібрування Лоренца (6.4) рівняння для потенціалів (6.7) і (6.8) здобувають наступний остаточний вигляд:

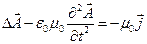(6.9)

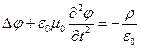(6.10)

Ці рівняння разом з визначеннями (6.1) – (6.2) еквівалентні рівнянням Максвела (5.1) – (5.4). Вони називаються неоднорідними хвильовими чи рівняннями Д’аламбера. Серед їхніх розв’язків потрібно вибрати такі, котрі задовольняють умові Лоренца (6.4). Таким чином, замість восьми (скалярних) рівнянь Максвела ми маємо чотири (скалярних) рівняння для потенціалів, математичні методи розв’язки яких розроблені значно краще, ніж для рівнянь (5.1) – (5.4).

Зауваження. Елементарний аналіз постійних e­ ₀ і m₀ показує, що постійна

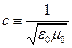(6.11)

має розмірність швидкості і її чисельне значення дорівнює: 300 000 км/с

Постійна С називається електродинамічної постійний. З врахуванням (6.11) рівняння (6.9) – (6.10) для електромагнітних потенціалів можна записати у вигляді:

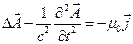, (6.9^/)

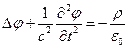, (6.10^/)

чи в символічному вигляді:

(6.9^//)

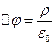(6.10^//)

де диференціальний оператор:

(6.13)

називається оператором Д’аламбера. Умова Лоренца (6.4) з врахуванням (6.11) записується у вигляді:

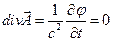(6.4^/)

Відомо, що однорідні хвильові рівняння описують поширення електромагнітних полів у вакуумі зі швидкістю, рівної с. Тому електродинамічна постійна с набуває фізичного сенсу швидкості електромагнітних хвиль у вакуумі. Так як світло має електромагнітну природу, то с можна вважати і швидкістю світла у вакуумі.

§7. Закони збереження для електромагнітних явищ.

Закони збереження енергії, імпульсу, моменту імпульсу й електричного заряду є фундаментальними законами фізики. Із сучасної теоретичної точки зору ці закони збереження вважаються наслідком різних симетрій фізичного світу: збереження енергії, імпульсу і моменту імпульсу – наслідок симетрії простору і часу (однорідності часу, однорідності і ізотропності простору); збереження електричного заряду є наслідок так званої каліброваної симетрії. (см. §6) рівнянь теорії поля (ця симетрія зв'язана не з властивостями простору-часу, а з внутрішніми властивостями самих фізичних полів; послідовний розгляд каліброваної симетрії можливо тільки в квантовій теорії поля). Ці точні закони збереження (і симетрії, що лежать у їхній основі) є більш загальними законами (принципами) фізики в порівнянні з конкретними рівняннями руху в різних фізичних теоріях. Тому всі інші закони фізики повинні узгоджуватися з законами збереження. Зокрема, з перерахованими вище законами збереження узгоджуються і рівняння термодинаміки. Іншими словами, із рівнянь Максвела повинні випливати закони збереження електричного заряду, енергії, імпульсу і моменту імпульсу для електромагнітних систем (тобто довільних систем електричних зарядів, що рухаються, разом з електромагнітними полями).

Почнемо з законузбереження електричного заряду. Рівняння Максвела (5.1) і (5.3), у котрі входить електричний заряд (у вигляді густини заряду 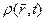і густини струму 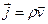), повинні бути сумісніз цим законом. Для перевірки цього застосуємо операції дивергенції до лівої і правої частин рівняння (5.1). Так як в силу тотожності divrot = 0, то ми при цьому одержимо:

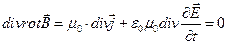
Змінюючи місцями операції div і 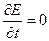в другому доданку, а потім позбавляючись від функції div 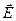за допомогою рівняння (5.3), одержуємо

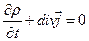
(7.1)

Рівняння (7.1) називається рівнянням безперервності і є законом збереження електричного заряду в диференціальній формі. Щоб переконатися в цьому, перетворимо (7.1) до інтегрального виду, проінтегрувавши його по довільному (але фіксованому) об'єму V:

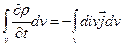
Переходячи в правій частині до інтегрування по поверхні за допомогою математичної теореми Гауса-Остроградского (2.19), а також змінюючи місцями операції 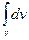й 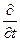у лівій частині, одержуємо:

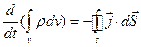(7.2)

де S - замкнута поверхня, що охоплює виділений об'єм V. Відзначимо, що в лівій частині (7,2) замість частинної похідної за часом ми пишемо повну похідну в силу фіксованості об'єму V (тобто область інтегрування від часу не залежить).

У співвідношенні (7.2) ліворуч стоїть зміна заряду в об'ємі V за одиницю часу, праворуч - кількість зарядів, що входять через поверхню S за одиницю часу. Рівність (7.2) цих двох величин і є закон збереження заряду. Знак "мінус" у формулі (7.2) є відображення того факту, що коли заряди виходять з об'єму, то кількість зарядів у цьому об'ємі зменшується і похідна за часом, є величина від'ємна.

Таким чином, ми переконалися, що рівняння безперервності (7.1) виражає закон збереження заряду і що рівняння Максвела (5.1)-(5.4) сумісні з цим законом (тому що (7.1) – наслідок рівняння Максвела).

Зауваження. В електрично ізольованій електромагнітній системі заряди з об'єму V не витікають. Тому на замкнутій поверхні S електричний струм відсутній, тобто 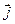│_S = 0. Тоді замість (7.2) одержуємо:

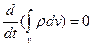чи ,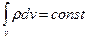

тобто заряд такої системи не змінюється.

Розглянемо тепер закон збереження енергії для електромагнітних явищ. Покажемо, що цей закон міститься (неявно) у рівняннях Максвела (5.1)-(5.4) і одержимо кількісне вираження для нього. Для цього помножимо скалярно рівняння (5.2) на вектор 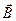, рівняння (5.1) – на вектор 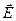і віднімемо з першого знайденого рівняння друге. У результаті одержимо співвідношення:

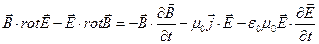
яке після застосування до лівої частини формули векторного аналізу:

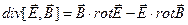(7.3)

можна записати у вигляді:

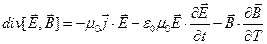(7.4)

скориставшись очевидними тотожностями:

,

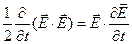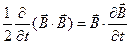
перепишемо (7.4) у вигляді:

,

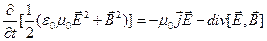чи, розділивши ліву і праву частини на m₀, у вигляді:

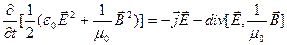(7.5)

Для спрощення запису (7.5) уведемо формально позначення:

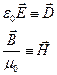(7.6)

після чого (7.5) записується в більш "симетричному" вигляді:

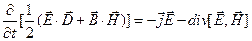(7.5^/)

Далі, уводячи позначення:

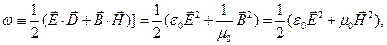(7.7)

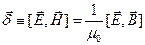(7.8)

перепишемо (7.5^/) у компактній формі

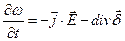, (7.5^//)

зручної для з'ясування фізичного змісту цього співвідношення.

Найпростіше з'ясувати фізичний зміст доданка 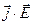у формулі (7.5^//):

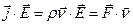(7.9)

де 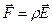є сила, що діє з боку електричного поля на заряд r в одиниця об'єму. Ясно тоді, що (7.9) є вираз для роботи, що виконує електричне поле по переміщенню зарядів в одиниця об'єму за одиницю часу. З іншої сторони ми знаємо, що магнітне поле не виконує роботи по переміщенню зарядів (це видно з закону Ампера: 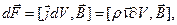відкіля випливає, що магнітна сила 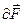перпендикулярна швидкості руху заряду r і отже робота магнітного поля 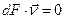). Тому можна вважати, що (7.9) є робота електромагнітногополя по переміщенню зарядів в одиниця об'єму за одиницю часу. Таким чином, електромагнітне поле має енергію і цю енергію може перетворюватися в кінетичну енергію зарядів. Може відбуватися і зворотний процес - випромінювання електромагнітний хвиль зарядами, що рухаються. Відповідно до (7.9) вираз:

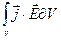(7.10)

є робота електромагнітного поля по переміщенню зарядів у довільному об'ємі V за одиницю часу.

Для з'ясування фізичного змісту рівняння (7.5^//) перетворимо його до інтегрального виду, проінтегрувавши його по довільному, але фіксованому об'єму V:

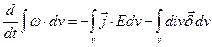
Переходячи в останньому доданку правої частини до інтегрування по поверхні S за допомогою формули (2.19), одержуємо співвідношення:

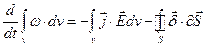, (7.11)

яке є інтегральна форма запису співвідношення (7.5^//).

Покажемо тепер, що співвідношення (7.5^//) і (7.11) є математичні вирази закону збереження енергії. Паралельно з'ясуємо фізичний зміст величин w, і 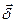, що входять у ці співвідношення. Для цього розглянемо дві часткові випадки електромагнітних систем.

1) Ізольована (замкнута) система. Тут ми розглядаємо таку фізичну систему (що складається з електромагнітного поля і зарядів), що не може обмінюватися енергією з іншими системами, що знаходяться поза виділеним об'ємом V. Це буває тоді коли розглянута система не взаємодіє з іншими системами і на поверхні S, що обмежує об'єм V, електромагнітне поле відсутнє, тобто 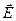│_S = 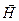│_S. У цьому випадку вектор 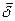(7.8) на поверхні S дорівнює нулю, отже і співвідношення (7.11) для ізольованої системи приймає вигляд: 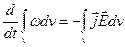(7.12)

так як згідно (7.10) у правій частині (7.12) стоїть робота виконувана електромагнітним полем по переміщенню зарядів в об'ємі V за одиницю часу, то (відповідно до загального закону збереження енергії) ліворуч у (7.12) повинне стояти відповідна зміна енергії електромагнітного поля за одиницю часу. Таким чином, ми дійдемо висновку, що інтеграл 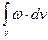визначає енергію електромагнітного поля в об'ємі V, а величина w, визначенна формулою (7.7), є густиною енергії електромагнітного поля, тобто енергія електромагнітного поля в одиничному об'ємі.

2) Відкрита система без зарядів. Тепер розглянемо електромагнітну систему, що не є ізольованою і складається тільки з електромагнітного поля в об'ємі V (тобто не містить електричних зарядів). Для такої системи r = 0, отже 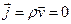і 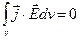. У цьому випадку (7.11) записується у вигляді:

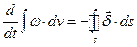(7.13)

Ми установили, що в лівій частині (7.13) стоїть зміна енергії електромагнітного поля в об'ємі V за одиницю часу. Оскільки енергія зникнути не може і поле не робить роботи по переміщенню зарядів у розглянутому випадку, то інтеграл по поверхні в правій частині (7.13) повинний визначати енергію електромагнітного поля, що витікаєз об'єму V за одиницю часу, тобто 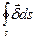є потік енергії електромагнітного поля через замкнуту поверхню S за одиницю часу. Звідси випливає фізичний зміст вектора 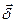це є густинапотоку енергії електромагнітного поля, тобто кількість енергії поля, що протікає в одиницю часу через одиничну площадку, перпендикулярну вектору 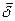. Вектор 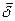, визначений формулою (7.8) називається вектором Умова-Пойтинга. Знак "-" у (7.13) указує, що енергія поля в об'ємі V зменшується, якщо потік енергії спрямований назовні з об'єму (тобто якщо потік позитивний - (див. визначення потоку вектора (2,15)).

У загальному випадку довільної електромагнітної системи співвідношення (7.11) показує, що зміна енергії електромагнітного поля в деякому об'ємі V дорівнює електромагнітної енергії, що витікає з V, і роботі виконаної полем по переміщенню зарядів усередині V. Таким чином, співвідношення (7.11) і, отже , співвідношення (7.5^//) є інтегральна і диференціальна форма запису закону збереження енергії для електромагнітних явищ.

Зауваження 1. Електромагнітне поле поряд з енергією володіє також і імпульсом. Імпульс електромагнітного поля 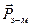в об'ємі V можна представити у вигляді інтеграла по об'єму від густини імпульсу 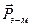(подібно тому як енергія W поля в об'ємі V можна виразити через густину енергії: ):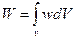