Тема 11. Контактные явления.

Работа выхода. Потенциал выхода. Потенциальная энергия электрона. Контактная разность потенциалов. Внешняя и внутренняя разность потенциалов. Эффект Зеебека. Эффект Пельтье.

Л. 1: § 9.60, § 9.62.

Тема 12. Контакт электронного и дырочного полупроводников.

Контакт полупроводников. p-n-переход. Основные и не основные носители тока. Изгибание электрических зон в области перехода. ВАХ p-n-перехода.

Л. 1: § 8.57.

Тема 13. Фотоэффект в полупроводниках.

Внутренний фотоэффект. Фотосопротивление, действие которого основано на внутреннем эффекте. Вентильный фотоэффект. Фото ЭДС. Применение внутреннего фотоэффекта: фотоэлектрические фотометры, экспонометры, люксметры.

Преобразователи солнечной энергии непосредственно в электрическую. Солнечные батареи.

Л. 1: § 2.9 Л. 2: § 10.36.

Тема 14. Люминесценция твердых тел.

Критерий длительности свечения Вавилова. Холодное свечение. Люминофоры. Изготовление кристаллофосфоров. Фотолюминесценция. Локальные уровни примеси – ловушки. Применение кристаллофосфоров – в электронно – лучевых (в частности, телевизионных) трубках, в люминесцентных лампах (лампах дневного света), аннигиляционных счетчиках заряженных частиц и для других целей.

Л. 1: § Л. 2: § 11.40.

Тема 15. Эффект Холла.

Электронная теория эффекта Холла. Постоянная Холла. Эффект Холла в полупроводниках. Определение концентрации носителей и подвижности носителей по измерениям постоянной Холла и проводимости s. Методы измерения эффекта Холла в многослойных (эпитаксиальных) структурах.

Тема 16. Кристаллическая решетка.

Структура кристаллической решетки. Решетки Бравэ. Решетки с базисом. Обозначение углов, направлений и плоскостей в кристалле (индексы Миллера).

Л. 1: § 6.45

Тема 17. Несовершенство и дефекты кристаллической решетки.

Мозаичная структура и границы зерен. Примеси. Дефекты по Френкелю и Шотки. Дислокации.

Литература (3, С 157 – 195, 197 – 228, 326 – 340)

МЕТОДИЧЕСКИЕ УКАЗАНИЯ.

В настоящем разделе дается знакомство с квантовыми статистиками Бозе – Эйнштейна и Ферми – Дирака. Предельным случаем этих статистик является статистика Больцмана – Максвелла. Будучи статистикой классической, она не учитывает спинавой характер микрочастиц, который подразделяются на фермионы с полуцелым спином, и бозоны со спином равным 0 или целому числу. Темы 10.4 – 10.15 посвящены изучению электрических, тепловых и оптических свойств металлов, полупроводников и диэлектриков. Объяснение контактных явлений в твердых телах ведется на основе квантово – механических представлений. Темы 10.16, 10.17 знакомят с кристаллической структурой твердых тел, кристаллографией и кристаллоструктурным анализом. Несовершенство и дефекты кристаллов изучаются на основании теории дефектов по Френкелю и Шоттки.

ОСНОВНЫЕ ФОРМУЛЫ.

Молярный объем кристалла:

V_m = M/r,

где М – молярная масса;

r - плотность кристалла.

Объем элементарной ячейки для решетки кубической сингонии:

V_ЭЛ = а³ ,

где а – параметр решетки.

Число элементарных ячеек в одном моле кристалла:

Z_m = V_m/V_ЭЛ, если кристалл состоит из одинаковых атомов, то:

Z_m = N_A/n,

где n – число одинаковых атомов, приходящихся на элементарную ячейку;

N_А – постоянная Авогадро.

Отношения числа элементарных ячеек к объему кристалла:

Z = Z_m/V_m;

если кристалл состоит из одинаковых атомов, то:

Z = rN_A/(nM).

Параметр кубической решетки из одинаковых атомов:

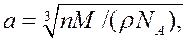
Расстояние между соседними атомами в кубической решетке:

1. 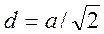(гранецинтрированной),

2. 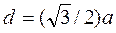(объемно – центрированной).

Средняя энергия квантового одномерного осциллятора

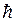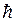< e > = e₀ + w/(e ^w/(RT) – 1),

где e₀ – нулевая энергия (e ₀ = 1/2 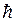w);

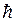– постоянная Планка ;

w - круговая частота колебаний осциллятора;

к – постоянная Больцмана;

Т – термодинамическая температура.

Молярная внутренняя энергия системы, состоящая из невзаимодействующих квантовых осцилляторов:

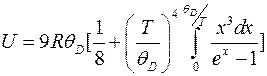
где R – молярная газовая постоянная;

Молярная теплоемкость кристаллического твердого тела по Дебаю:

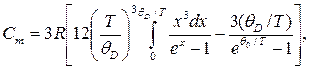
где q_D – характеристическая температура Дебая (q_D = 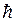w_max/k).

Молярная теплоемкость кристаллического твердого тела в области низких температур (предельный закон Дебая):

С_m = (12 p⁴/5) R (T/q_D)³ = 234 R(T/q_D)³ (T >> q_D),

Теплота, необходимая для нагрева тела:

,

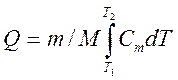где m – масса тела;

М – молярная масса;

T₁ и T₂ – начальная и конечная температуры тела.

Распределение свободных электронов в металле по энергиям при О К

dn (e ) = (1/2p²) (2m / h²)^3/2

e_F = (h²/2m) (3p² n)^2/3 ,

где n – концентрация электронов в металле.

Удельная проводимость собственных полупроводников:

g = en(b_n + b_p), где e – элементарный заряд;

n – концентрация носителей заряда ( электронов и дырок );

b_n и b_p – подвижности электронов и дырок.

Напряжение на гранях прямоугольного образца при эффекте Холла, холловская разность потенциалов:

U_н = R_нBja,

где R_н – постоянная Холла;

B – магнитная индукция;

j – плотность тока;

a – ширина пластины ( образца ).

Постоянная Холла для полупроводников типа алмаз, германий, кремний, и др., обладающих носителями заряда одного вида (n или p):

R_н = 3p/(8en),

где n – концентрация носителей заряда.

Связь магнитной индукции B с напряженностью Н магнитного поля в изотропном магнетике:

B = mm₀H,

где m - магнитная проницаемость среды;

m₀ – магнитная постоянная.

Намагниченность однородного изотропного магнетика:

J = ,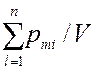

где 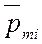– магнитный момент i – молекулы (атома);

N – число молекул в объеме V.

Молярная намагниченность однородного изотропного магнетика:

,

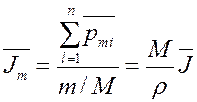где m – масса магнетика;

M – молярная масса;

r - плотность магнетика;

Удельная намагниченность однородного изотропного магнетика:

.

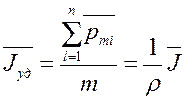Магнитная восприимчивость однородного изотропного магнетика:

c = J/H, где Н – напряженность магнитного поля.

Молярная магнитная восприимчивость однородного изотропного магнетика: c_m = J_m/ H = Mc/r.

Удельная магнитная восприимчивость однородного изотропного магнетика: c_уд = J_уд/H = c/r.

Связь магнитной восприимчивости с магнитной проницаемостью:

m = 1 + c.

Намагниченность при насыщении в случае однородного изотропного магнетика: ,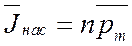

где n – концентрация молекул атомов с магнитным моментом p_m.

Магнитная восприимчивость парамагнитного однородного изотропного магнетика при условии p_mB << kT: c = m₀np²_m/(3kT),

где к – постоянная Больцмана;

Т – термодинамическая температура.

Магнетон Бора: m_в = 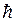е/(2m_e),

где m_e – масса электрона; m_в = 0,927.10^-23Дж/Тл.

Частота прецессии Лармора: w_l = eB/ (2m_e),

где B – магнитная индукция.