Еоретична частина. Розділ 1.1, 1.3, 1.5.
абораторна робота №5

ВИВЧЕННЯ ОСНОВНОГО РІВНЯННЯ ДИНАМІКИ ОБЕРТАЛЬНОГО РУХУ
 ТВЕРДОГО ТІЛА
ТВЕРДОГО ТІЛА
Мета роботи
| Експериментально перевірити основне рівняння динаміки обертального руху твердого тіла. |
Прилади та обладнання
| Маятник Обербека, секундомір, різноважки (тіла різної маси ), штанґенциркуль, міліметрова лінійка |
Опис вимірювального пристрою
Маятник Обербека (рис.1) складається з чотирьох стрижнів (1), закріплених на втулці (2) під прямими кутами. Вздовж стрижнів можуть фіксовано пересуватися чотири однакові циліндри (3).
|

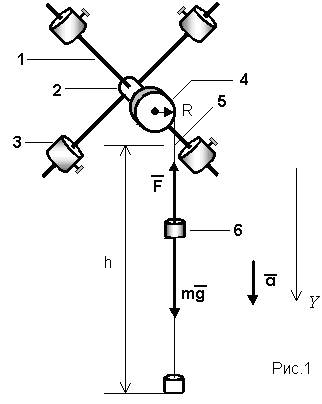
 Втулка і шків (4) радіуса R насаджені на спільний горизонтальний вал, що кріпиться у підшипниках до вертикального стояка. На шків намотується нитка (5), до кінця якої прикріплюються тіла (6) різних мас m (на основний вантаж можна накладати одну або дві різноважки). Якщо обертальна система відцентрована, то поступальний рух тіл масою m і обертальний рух маятника будуть рівноприскореними. Виведення розрахункових формул Другий закон Ньютона для тіла, яке опускається на нитці, в проекції на вісь Y (Рис.1): mα= mg–F,(1) де F - сила натягу нитки. Якщо експериментально виміряти час t проходження тілом відстані h, то з формули шляху рівноприскореного руху без початкової швидкості можна обчислити прискорення тіла: Втулка і шків (4) радіуса R насаджені на спільний горизонтальний вал, що кріпиться у підшипниках до вертикального стояка. На шків намотується нитка (5), до кінця якої прикріплюються тіла (6) різних мас m (на основний вантаж можна накладати одну або дві різноважки). Якщо обертальна система відцентрована, то поступальний рух тіл масою m і обертальний рух маятника будуть рівноприскореними. Виведення розрахункових формул Другий закон Ньютона для тіла, яке опускається на нитці, в проекції на вісь Y (Рис.1): mα= mg–F,(1) де F - сила натягу нитки. Якщо експериментально виміряти час t проходження тілом відстані h, то з формули шляху рівноприскореного руху без початкової швидкості можна обчислити прискорення тіла: 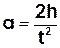 . (2) Використавши зв’язок між танґенціальним прискоренням точок на ободі диску, яке дорівнює прискоренню вантажу m, і кутовим прискоренням диску: α= . (2) Використавши зв’язок між танґенціальним прискоренням точок на ободі диску, яке дорівнює прискоренню вантажу m, і кутовим прискоренням диску: α=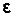 R,(3) одержимо вираз для кутового прискорення маятника: R,(3) одержимо вираз для кутового прискорення маятника: 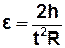 . (4) Обертальний момент сили, що викликає це прискорення: . (4) Обертальний момент сили, що викликає це прискорення: 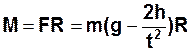 , (5) або через кутове прискорення: M=m(g– , (5) або через кутове прискорення: M=m(g–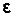 R)R .(6) R)R .(6) |
Отже, виконуючи експерименти з маятником Обербека, можна знаходити моменти сил, що діють на обертальну систему, та кутові прискорення системи.Оскільки крім моменту сили натягу нитки на систему діє ще момент сили тертя Mт, то експеримент зведеться до перевірки рівняння:
М–Мт = J 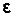 , (7)
, (7)
яке можна подати у вигляді:
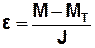 . (8)
. (8)
З формули (8) видно, що залежності, які випливають з рівняння (8),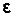 =f(M) та
=f(M) та 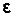 =
= 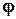 (1/J),повинні мати лінійний характер.
(1/J),повинні мати лінійний характер.
При підготовці до виконання роботи використати:
еоретична частина. Розділ 1.1, 1.3, 1.5.
Послідовність виконання роботи
| Завдання 1: експериментальна перевірка залежності кутового прискорення e маятника Обербека від моменту зовнішніх сил |
1. Тричі виміряти висоту опускання тіла hі записати у Табл. 1.
2. Три рази виміряти діаметр шківа d, результати записати у Табл.1.
3. Закріпити циліндри на мінімальній відстані від осі обертання.
4. Три рази виміряти час опускання основного вантажу;
результати записати у Табл. 2.
5. Дії, вказані в п.4, повторити ще два рази для більших мас m.
Для цього на основний вантаж, прикріплений до нитки, треба
накласти спочатку одну, а потім дві різноважки.
6. Перевівши результати вимірювань всіх величин в одиниці СІ,
за формулами (4), (5) розрахувати величини M i 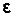 (для трьох
(для трьох
значень мас m ) Записати одержані значення в Табл. 3.
7. Побудувати графіки залежності 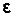 від М.
від М.
8. Обчислити похибки вимірювання кутового прискорення за
формулою :
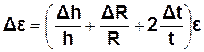 (9)
(9)
та записати їх в Табл. 3.
9. Відкласти в масштабі, вибраному для 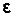 , відрізки ±
, відрізки ± 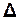
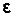 навколо
навколо
відповідних експериментальних точок ґрафіку
10. Провести через експериментальні точки ґрафіку найбільш
оптимальним способом пряму та знайти числове значення
моменту сил тертя Мт як точку перетину прямої з віссю моментів
сил. Записати це значення в Табл.3.
11. Перемістити циліндри на середину кожного з чотирьох
стрижнів, зафіксувати їх і виконати дії, вказані в пунктах 3-10.
12. Зафіксувати циліндри в крайніх положеннях і ще раз повторити
дії, вказані в пунктах 3-10.
| G | Графіки залежності 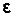 від М, одержані для трьох розміщень циліндрів на стрижнях, будувати на одних і тих координатних осях. від М, одержані для трьох розміщень циліндрів на стрижнях, будувати на одних і тих координатних осях. |
Завдання 2: експериментальна перевірка залежності кутово- го прискорення 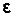 від моменту інерції J маятника Обербека при постійному моменті сил. від моменту інерції J маятника Обербека при постійному моменті сил. |
1. Обчислити моменти інерції маятника Обербека при різних
положеннях циліндрів на стрижнях як відношення приростів DМ
до D 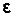 ґрафіків
ґрафіків 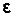 =f (М), побудованих у завданні 1.
=f (М), побудованих у завданні 1.
2. Для фіксованого значення моменту сили М1 виписати значення
кутового прискорення 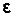 з трьох попередніх таблиць. Хоча
з трьох попередніх таблиць. Хоча
теоретично, згідно з (6), момент сили залежить від кутового
прискорення, однак в наших експериментах величина 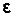 дуже мала
дуже мала
і момент сили практично дорівнює: М = mgR.
3. Побудувати ґрафік залежності кутового прискорення 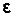 від
від
величини, оберненої до його моменту інерції. Виконати
аналогічні побудови для двох інших моментів сил М2 і М3.
Таблиці результатів вимірювань і розрахунків
аблиця 1
| № | h, мм | Δh, мм | d, мм | Δd, мм | R, мм | ΔR, мм |
| вимір | розрах. | вимір | розрах. | |||
| вимір | розрах. | вимір | розрах. | |||
| вимір | розрах. | вимір | розрах. | |||
| сер. | розрах. | розрах. | розрах. | розрах. | розрах. | розрах. |
аблиця 2
| № | m = 0,220кг | m = 0,303кг | m = 0,386кг | |||
| t, с | Δt, с | t, с | Δt, с | t, с | Δt, с | |
| вимір | розрах | вимір | розрах | вимір | розрах | |
| вимір | розрах | вимір | розрах | вимір | розрах | |
| вимір | розрах | вимір | розрах | вимір | розрах | |
| сер. | розрах. | розрах. | розрах. | розрах. | розрах. | розрах. |
аблиця 3
| m, кг | 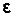 , с-2 , с-2 | M, Н·м | 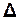 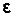 , c-2 , c-2 | Мт, Н·м |
| 0,220 | розрах. | розрах. | розрах. | розрах. |
| 0,303 | розрах. | розрах. | розрах. | розрах. |
| 0,386 | розрах. | розрах. | розрах. | розрах. |
| G | Таблиці 2 і 3 складати окремо для кожного з трьох розміщень циліндрів на стрижнях. |
аблиця 4
| Розміщення циліндрів | J, кг·м2 | 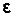 , с-2 , с-2 | 1/J, кг-1м-2 |
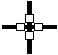 | розрах. | розрах. | розрах. |
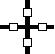 | розрах. | розрах. | розрах. |
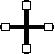 | розрах. | розрах. | розрах. |
Контрольні запитання
1. Що називається моментом інерції тіла ?
2. Записати і пояснити основне рівняння динаміки обертального
руху твердого тіла.
3. Що називається моментом сили відносно осі обертання ?
4. Що називають плечем сили ?
5. У чому полягає суть перевірки основного рівняння динаміки в даній лабораторній роботі ?
6. Як визначається момент інерції у даній роботі ?
7. Вивести формулу, що описує обертальний момент, діючий на маятник Обербека.
Рекомендована література
1. Курс фізики / За редакцією І.Є.Лопатинського.
– Львів: Вид. «Бескид Біт», 2002.
2. Трофимова Т.И. Курс физики.– М.: Высшая школа, 1990.
3. Савельев И. В. Курс общей физики, т.1 –М.: Наука, 1982.
