Теорема и ряд Котельникова

Б.И. Филиппов

Теория электрической связи

Учебное пособие

Рекомендуется для студентов телекоммуникационных вузов, изучаюших теорию и практику передачи информации по каналам связи

по направлению подготовки дипломированных специалистов 552500,

654200 (радиотехника), 550400 (телекоммуникации), по направлению общепрофессиональных дисциплин (ОПД) – «Теория электрической связи»,

«Радиотехнические цепи и сигналы» и др.

Новосибирск

УДК 621.391 (075)

ББК 32.81

Б.И. Филиппов

Теория электрической связи

Т33 2011. – 284 с.: ил.

Данная книга состоит из двух частей.

В первой части излагаются физические явления в нелинейных электрических и параметрических цепях, применяемых в системах связи. Выявляются основные характеристики и особенности схем нелинейных устройств, рассматриваются различные математические методы, применяемые при расчете таких цепей и устройств. Кроме того, в этой части рассматриваются случайные процессы, их представление, вероятностные и числовые характеристики.

Во второй части рассматривается теория передачи сигналов как единая научная дисциплина, основу которой составляют теория сигналов, теория помехоустойчивости и теория информации.

Излагаются общие закономерности передачи информации по каналам связи, определяются потенциальные возможности способов передачи и приема сигналов, сравниваются различные системы связи между собой.

Книга предназначена для студентов электротехнических университетов связи и инженеров, работающих в области радиотехники и связи.

Рецензенты: зав.кафедрой САПР СибГУТИ,

д.т.н., профессор Сединин В.И.

ученый секретарь ФГУП “СНИИМ”

д.т.н.,профессор, действительный член

Россияской метрологической академии

Пальчун Ю.А.

Предисловие

Настоящий учебник составлен в соответствии с программой по курсу «Теория электрической связи». В основу учебника положены лекции, читавшиеся автором в Сибирском Государственном Университете Телекоммуникаций и Информатики (СибГУТИ), г. Новосибирск. В работе были использованы учебные пособия, написанные проф. А.А. Макаровым и доц. Л.А. Чиненковым кафедры Радиотехнических систем СибГУТИ.

Курс теории электрической связи базируется на материалах теории линейных и нелинейных электрических цепей, теории случайных процессов и призван создать общие основы для изучения студентами с единых позиций современной теории связи. Автор стремился там, где это возможно, освободить изложение от обилия математических фактов и строгости в доказательствах с целью сделать ясным физическое толкование полученных результатов. С этой же целью основные положения теории иллюстрируются конкретными примерами из различных областей техники связи.

В работе над книгой большую помощь оказали автору сотрудники кафедры радиотехнических систем СибГУТИ. Ценные замечания были сделаны проф. В.И. Седининым и проф. Ю.А. Пальчуном. Пользуясь случаем, автор выражает всем, способствующим улучшению книги, свою искреннюю благодарность.

Автор

Часть I. Теория нелинейных электрических цепей

1. Задачи курса ТЭС

Общие сведения о курсе

Курс «Теория электрической связи» (ТЭС) относится к числу фундаментальных дисциплин подготовки высококвалифицированных инженеров, владеющих современными методами анализа и синтеза систем и устройств связи различного назначения. В нем принят единый методологический подход к решению задач электросвязи на основе вероятностных представлений.

Целью курса является изучение основных закономерностей и методов передачи информации по каналам связи. В курсе рассматриваются:

1) способы математического представления сообщений, сигналов и помех;

2) методы формирования сигналов и их преобразования в электрических цепях;

3) вопросы анализа помехоустойчивости и пропускной способности систем электросвязи;

4) методы помехоустойчивого кодирования, оптимального приема сообщений;

5) принципы многоканальной передачи и распределения информации в сетях связи;

6) вопросы оптимизации систем электросвязи.

Курс ТЭС базируется на таких дисциплинах, как высшая математика, физика, теория электрических цепей (ТЭЦ), электроника, квантовые приборы и микроэлектроника, вычислительная техника и программирование.

Курс ТЭС вместе с курсом ТЭЦ составляют теоретическую основу техники связи, элементы которой изучаются в последующих инженерных дисциплинах.

Общие сведения о системах электросвязи

Передача сообщений на расстояние из одного пункта в другой может быть осуществлена с помощью какого-либо материального носителя (бумаги, магнитной ленты, диска, флэш-карты и др.) перемещаемого в пространстве, либо с помощью физического процесса, способного распространятся на расстояния (электрический ток, звуковые и электромагнитные волны и др.). Физический процесс, несущий передаваемое сообщение из точки в точку, называется сигналом.

В процессе передачи по системе связи сообщение может подвергаться многочисленным преобразованиям, существенно меняющим его электрическое представление и физические характеристики. Однако, следует иметь в виду, что объектом передачи является не электрическое представление сообщения, а та полезная информация, содержащаяся в передаваемом сообщении, которая должна оставаться неизменной при всех преобразованиях.

Информацией называется совокупность сведений о каком-либо явлении, событии или объекте, которые увеличивают знания получателя о них.

Если в системах для передачи сообщений в качестве несущих используются электрические или электромагнитные сигналы, то такие системы называются системами электросвязи, в отличие от звуковых, гидроакустических и других систем связи. Обобщенная структурная схема простейшей системы электросвязи изображена на рис. 1.1.

Рисунок 1.1. Обобщенная структурная схема системы связи

Источник сообщения – человек, автомат, ЭВМ, датчик. Сообщениями могут быть: речь (системы телефонной связи); текст (системы телеграфной связи); неподвижное изображение (фототелеграфные системы связи); подвижные изображения (телевизионные системы связи); параметры каких-либо устройств (системы телеметрии); команды управления каким-либо устройствами (системы телеуправления); данные (системы передачи данных).

Кодирующее устройство (кодер) в общем случае осуществляет:

1) преобразование сообщения, поступающего от источника сообщений, в первичный электрический сигнал;

2) преобразование в случае необходимости, непрерывного сигнала в дискретный;

3) статистическое (эффективное) кодирование с целью увеличения скорости передачи информации (устранение избыточности в сообщении);

4) помехоустойчивое кодирование (введение избыточных символов) с целью повышения помехоустойчивости системы связи.

Генератор несущего колебания – формирует электрические колебания, которые являются переносчиком сообщения. Сигналом – переносчиком обычно служит либо гармоническое колебание, либо периодическая последовательность импульсов, либо шумоподобный сигнал.

Модулятор – изменяет один (или несколько) параметров сигнала переносчика в соответствии с модулирующим сообщением, поступающим от кодера. В процессе модуляции могут изменяться амплитуда, частота или фаза гармонической несущей; амплитуда, длительность импульсов, частота следования, фаза импульсного переносчика; тип использования шумоподобного сигнала. Иногда одновременно может осуществляться модуляция нескольких параметров сигнала-переносчика.

Выходное устройство ограничивает спектр частот передаваемого сигнала для устранения помех от соседних по частоте сигналов и увеличения эффективности использования полосы частот; обычно увеличивает мощность сигнала для обеспечения требуемой помехоустойчивости приема информации, передает сигнал в среду распространения. Таким образом, выходное устройство содержит полосовые фильтры, усилитель мощности и излучатель сигнала. Кодирующее устройство, модулятор, генератор несущего колебания и выходное устройство образуют передатчик.

Линия связи – совокупность технических средств (физическая цепь, волновод, кабель и т.п.), либо окружающая среда, через которые сигнал поступает от передатчика к приемнику. В линии связи сигнал претерпевает изменения из-за воздействия помех и искажений.

Помехи – это всякое постороннее воздействие на сигнал, препятствующее правильному приему (флуктуационный тепловой шум, атмосферные помехи, помехи от других передатчиков и т.п.).

Входное устройство – выделяет из линии связи сигнал нужного (требуемого) передатчика и усиливает его до необходимого уровня. Таким образом, входное устройство содержит полосовые фильтры и усилители.

Демодулятор (детектор) – преобразует принятый модулированный сигнал в сообщение, которым осуществлялась модуляция, и содержащее переданную информацию.

Декодер – производит обратное преобразование принятых сигналов (кодовых комбинаций) в исходное сообщение.

Получатель сообщения – человек, автомат, ЭВМ, реле и т. п.

Входное устройство, детектор, декодер образуют приемник.

Основная задача совершенствования систем связи состоит в том, на передаче за счет модуляции и кодирования создать сигнал, наименее подверженный действующим помехам и искажениям, а на приеме за счет фильтрации, детектирования и декодирования выделить передаваемое сообщение с наименьшими искажениями.

Наряду с понятием «система связи» часто оперируют более узким понятием – «канал связи». Это совокупность технических средств (включая линию связи), обеспечивающих передачу сообщений от источника к получателю.

Практика построения систем связи показала экономическую целесообразность использования ее многими абонентами, что приводит к созданию многоканальных систем связи. Это, несомненно, усложняет системы связи, т. к. требует объединения сигналов разных абонентов на передаче и, самое трудное, разделение их на прием без заметных взаимных помех.

Система связи, позволяющая осуществлять передачу сообщений только в одну сторону, называется односторонней (симплексный режим). В случае двухстороннего обмена потребуется система связи для передачи сообщений в противоположном направлении (дуплексный режим).

Практически классической является задача обмена между многими (сотнями и тысячами) отправителей и получателей в самых различных комбинациях. В этом случае используемые системы связи объединяются в сеть связи. Наиболее перспективное построение систем связи (при большом числе абонентов) связано с использованием электронных узлов коммутации, когда связь между абонентами осуществляется через один или несколько узлов коммутации с использованием систем связи различного типа, т. е. сети связи, которая имеет конечной целью передачу любой информации в любую точку страны (мира). Эта информация будет в основном цифровой. Как будет показано далее, цифровой сигнал является универсальным и позволяет передавать все виды сообщений, включая и телевизионные. Коммутация сообщений в сети связи осуществляется с помощью кодированных сигналов и ЭВМ при использовании существующих каналов связи (спутниковых, радиорелейных, кабельных, оптических и др.).

Кодер + Декодер = Кодек

Модулятор + Демодулятор = Модем

Кодер + Декодер + Модулятор + Демодулятор = Кодем

2. Сигналы связи

2.1. Формирование и преобразование сигналов. Кодирование и декодирование. Модуляция и демодуляция

Сигналы – в широком смысле физические явления, колебания, процессы осуществляющие перенос информации из одного пункта в другой, т.е. это переносчик сообщения (информации).

Электрический сигнал – некоторое электрическое возмущение отображающее передаваемое сообщение.

Таким образом, под сигналом будем понимать функцию времени, в которую тем или иным образом «вложено» передаваемое сообщение.

В радиотехнике (и радиотехнических системах) сообщения передаются посредством радиоволн, т. е. электромагнитного поля. Его мы и будем называть сигналом (радиосигналом).

Информация → сообщение → сигнал

U(t) S(t)

Рисунок 2.1. Сущность преобразования информации в сигнал

2.2. Классификация сигналов и их основные свойства

С информационной точки зрения сигналы могут быть:

1) детерминированными;

2) случайными.

Критерием такой классификации является возможность или невозможность предсказания их мгновенных значений в любые моменты времени.

Детерминированные – такие сигналы, для которых математическим описанием является заранее известная (определенная) функция времени, т. е. позволяющая предсказать мгновенное значение в любой момент времени 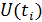с вероятностью 1.

Примеры:

1) ,

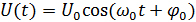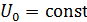– амплитуда,

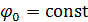– начальная фаза,

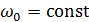– частота,

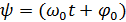– полная фаза.

2)

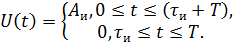
Рисунок 2.2. Последовательность однополярных прямоугольных импульсов

Случайные сигналы – такие сигналы, математическое описание которых является случайной функцией времени, т. е. мгновенные значения этих сигналов заранее неизвестны и могут бить предсказаны лишь с некоторой вероятностью .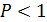

Примеры: сигналы речи, музыки, параметры последовательности принимаемых радиоимпульсов на входе радиолокационного приемника ( , , ).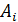

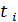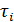Строго говоря, детерминированных сигналов в природе не существую, т.к. полностью известные сигналы не содержат в себе информации.

Реальные сигналы являются случайными по двум основным причинам:

а) случайной природой сообщений;

б) случайным характером помех, воздействующих на сигнал при его передаче. Математическое описание сигналов базируется на аппарате теории вероятностей, теории случайных процессов и математической статистике.

Значение детерминированных сигналов – при определенных условиях модель детерминированного сигнала может быть применена как более простая, например, при 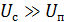. Кроме того, часть параметров сигнала являются детерминированными.

По виду временной функции

а) непрерывные;

б) дискретные;

в) цифровые;

г) импульсные.

Рисунок 2.3. Варианты структуры сигналов

Рисунок 2.4. Четыре класса сигналов

Особой разновидностью дискретных сигналов являются цифровые сигналы – у них отсчетные значения представляются в форме чисел (обычно в двоичной системе счисления по соображениям простоты аппаратурной реализации и обработки). Двоичная система счисления идеально подходит для описания импульсных последовательностей.

Рассмотренные виды сигналов используются в реальных системах связи.

В частности, дискретизация непрерывного сигнала по времени производится по теореме Котельникова, а квантование сигналов по уровню использует ИКМ (импульсно кодовая модуляция). Сигнал ИКМ – цифровой сигнал.

Пример:

Для речевого сигнала длина кодовой комбинации 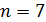, тогда число уровней 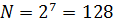, и в разные моменты времени ;

.

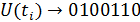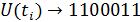Импульсные сигналы – важный для техники связи класс сигналов (например, рис. 2.5).

Рисунок 2.5. а) видеоимпульсы;

б) радиоимпульсы

По физическим характеристикам любой сигнал связи характеризуется рядом основных физических характеристик, необходимых для определения требований к каналу связи, по которым они передаются (рис. 2.6).

Рисунок 2.6

Основные характеристики сигнала:

1) длительность сигнала – ;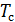

2) ширина спектра – ;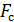

3) динамический диапазон – .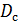

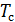– интервал времени, в пределах которого сигнал существует.

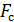– характеризует скорость изменения сигнала на интервале .

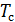Рисунок 2.6. а) быстро меняющаяся функция;

б) медленно меняющаяся функция

Чем выше скорость изменения функции, тем шире спектр: .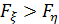

Спектр одиночного импульса:

Рисунок 2.7. Представление модуля функции типа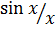

Практически (и теоретически) большинство сигналов имеют бесконечный спектр. Тогда, казалось бы, ширина полосы пропускания канала должна быть бесконечна. Реально это не так.

Под полосой сигнала 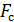понимают ту полосу частот 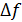, в пределах которой сосредоточена основная энергия (мощность) сигнала.

, ,

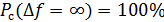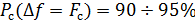где 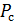– мощность сигнала.

Динамический диапазон сигнала 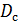определяется выражением:

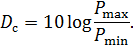
Рисунок 2.8. Пределы изменения уровня (напряжения) сигнала

Физический объем сигнала – обобщенная характеристика сигнала связи ( ).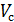

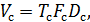
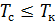– время, в течение которого канал занят сигналом,

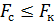– полоса пропускания канала связи,

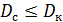– динамический диапазон сигнала, который пропускает канал связи с допустимыми искажениями.

По виду передаваемого сообщения

Вид сигнала определяется видом сообщения:

1. Телефонный (речевой) сигнал.

2. Телеграфный сигнал.

3. Фототелеграфный сигнал.

4. Передача данных.

5. Сигнал вещания.

6. Телевизионный сигнал.

Телефонный сигнал

Формируется микрофоном.

Речь имеет диапазон частот 50 ÷ 10000 Гц.

Основные требования – разборчивость, натуральность окраски.

МККТТ (Международный консультативный комитет по телефонии и телеграфии) рекомендует ограничить полосу частот 0,3 ÷ 3,4 кГц; 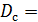25 ÷ 35 дБ.

Телеграфный сигнал

Рисунок 2.9. а) однополярные импульсы;

б) двуполярные импульсы

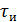– определяет скорость передачи сообщения.

Скорость передачи: 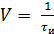[Бод].

Полоса частот: 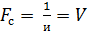[Бод].

1 Бод = 1 Илл/сек.

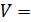50, 100, 200Бод –скорость передачи.

Сигнал передачи данных

Аналогичен телеграфному сигналу, но отличается более высокой скоростью передачи.

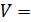600, 1200, 2400, 4800, 9600 Бод.

Фототелеграфный сигнал

Используется при передаче неподвижных изображений (фото, полос газет, чертежей, карт погоды). В факсимильных аппаратах скорость вращения барабанов:

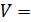60, 90, 120 (Оборот/минута),

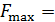732, 1100, 1465 Гц соответственно,

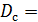25 дБ.

Сигнал звукового вещания

Речь диктора 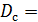25 ÷ 35 дБ.

Художественное чтение 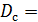40 ÷ 50 дБ.

Симфонический оркестр 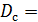65 дБ.

Спектр сигнала звукового вещания 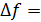30 ÷ 15000Гц.

Телевизионный сигнал

Отличается от факсимильной передачи тем, что изображение подвижно.

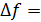0 ÷ 6 МГц, 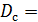40 дБ.

2.3. Кодирование, декодирование. Модуляция и демодуляция

Это основные преобразования сигналов в системах связи при передаче сообщений от источника к получателю.

Кодирование используется при передаче дискретных сообщений, а также при передаче непрерывных сообщений цифровым методом (ИКМ). Кодирование – это представление элементов дискретного общения в виде кодовых комбинаций по определенному правилу соответствия.

Кодовая комбинация– совокупность элементов.

Пример: телеграфный код № 2 (две комбинации):

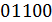
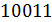
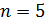– число элементов в кодовой комбинации,

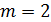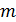код двоичный ( , где – основание кода).

В вычислительной технике используется 32-х и более элементный код.

Декодирование – обратное преобразование для восстановления сообщения из принятого сигнала.

Модуляция– преобразование первичного сигнала сообщения в другой сигнал наиболее пригодный для передачи по каналам связи, т.е. наилучшим образом согласованный по своим характеристикам линии связи с характеристикой линии связи. Для модуляции используется (по существу это перенос спектра сигнала) гармонический переносчик более высокой частоты (несущей).

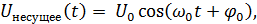
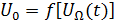– амплитудная модуляция,

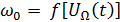– частотная модуляция,

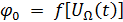– фазовая модуляция.

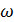– высокие частоты (ВЧ),

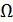– низкие частоты (НЧ),

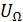– модулирующий сигнал.

Демодуляция – преобразование ВЧ модулированного сигнала в НЧ немодулированный. Сигнал на выходе демодулятора примерно соответствует сигналу на входе модулятора.

2.4. Детерминированные (регулярные) сигналы и их классификация

Детерминированные (регулярные) сигналы описываются известными функциями времени. Реальные сигналы и помехи – случайные функции времени.

Детерминированные сигналы применяются:

1. При возможных измерениях и испытаниях систем связи.

2. В технике связи случайные сигналы обычно являются отрезками (отдельными реализациями) регулярных сигналов.

Детерминированные сигналы делятся на:

1. Периодические.

2. Непериодические.

3. Почти периодические.

Периодический сигнал

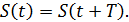
Рисунок 2.10. Периодическая последовательность импульсов сложной формы

Разложим сигнал 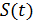в ряд Фурье:

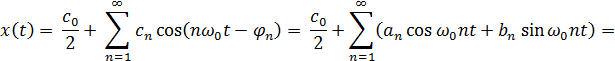
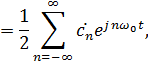
где:

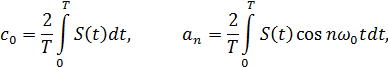
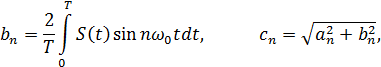
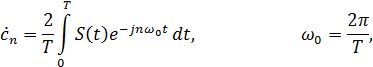
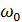– основная частота сигнала (первая гармоника),

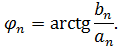
Непериодические сигналы (описываются непериодическими функциями времени) имеют сплошной спектр. Для его разложения используется преобразование Фурье.

Прямое преобразование Фурье:

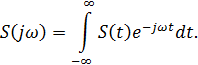
Обратное преобразование Фурье:

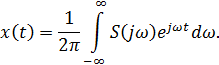
Почти периодические сигналы

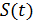– непрерывный по времени сигнал,

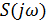– дискретный спектр сигнала.

Это модулированные сигналы.

2.5. Разложение сигналов в ряд по ортогональным функциям

Для исследования различных свойств сообщений, сигналов и помех удобно использовать разложение этих процессов в ряды.

Любой процесс (с некоторыми математическими ограничениями) можно представить в виде ряда:

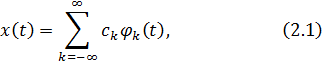
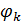– ортогональные простейшие функции, неслучайные. Например:

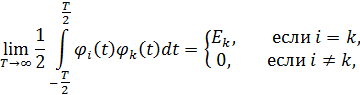
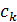– случайный коэффициент:

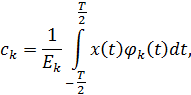
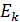– энергия ортогональных функций.

Если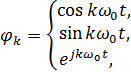

то ряд (2.1) Фурье:

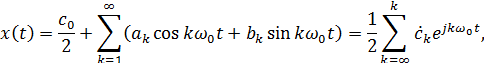
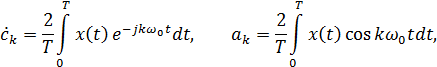
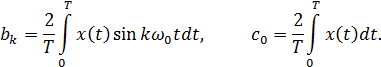
Теорема и ряд Котельникова

Радиотехнические сигналы подразделяются на непрерывные и дискретные. Непрерывные сигналы (функции) могут принимать любые, сколь угодно близкие друг к другу значения, в любые моменты времени. Примером непрерывного сигнала является гармоническое колебание.

Дискретные (цифровые) сигналы могут принимать только заранее известные значения, отличающиеся одно от другого на конечную величину, причем изменяться эти значения могут только в определенные моменты времени. Примером дискретного сигнала является (рис. 3.1) периодическая последовательность прямоугольных импульсов, которая в момент времени 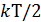принимает значения 0 или .

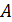Рисунок 3.1. Периодическая последовательность прямоугольных однополярных импульсов

Любая непрерывная функция, спектр которой не содержит частот выше 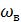, полностью определяется своими отсчетами, взятыми через интервал времени – теорема Котельникова.

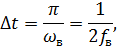
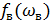– наивысшая частота спектра сигнала.

Рисунок 3.2. а) последовательность отсчетов непрерывной функции;

б) ограничение спектра непрерывной функции

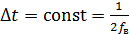– интервал Котельникова,

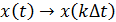– аппроксимирующая функция.

Доказательство: теорема Котельникова основывается на преобразовании Фурье:

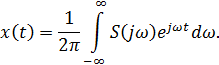
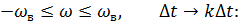
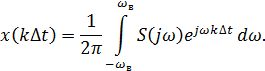
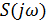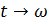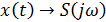Далее теорема Котельникова основывается на разложении функции в комплексный ряд Фурье, на осуществлении перехода от , от и от .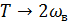

С математической точки зрения теорема Котельникова означает представление сигнала в виде ряда:

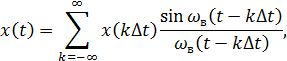
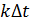– отсчеты, ( ),

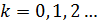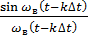– функция отсчетов.

Ряд Котельникова– это разложение сигнала 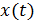в ряд по ортогональным функциям:

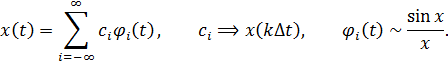
Выводы:

1. Ряд Котельникова является основание для восстановления на приеме непрерывного сигнала по отсчетам.

2. Ряд Котельникова лежит в основе всех импульсных способов передачи сигналов.

ИКМ – импульсно-кодовая модуляция,

АИМ – амплитудно-импульсная модуляция,

ШИМ – широтно-импульсная модуляция,

ФИМ – фазоимпульсная модуляция.

Замечание:

1. 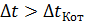– нельзя, т.к.:

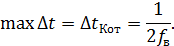
Иначе будет потеряна информация об исходном сообщении.

2. 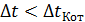можно, но точность передачи не возрастет; если

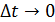, то .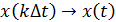

3.1. Восстановление непрерывного сигнала по отсчетам

Для восстановления исходного непрерывного сигнала из импульсов – отсчетов надо эти импульсы подать на вход идеального фильтра нижних частот (ИФНЧ), который имеет следующие характеристики.

Амплитудно-частотная характеристика идеального ФНЧ (АЧХ ИФНЧ) имеет вид:

Рисунок 3.3. АЧХ ИФНЧ

Идеальная реакция ИФНЧ, т.е. реакция на дельта-импульс, имеет вид:

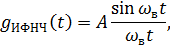
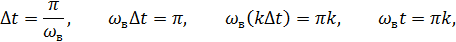
Формула (3.2) определяет точки, где функция 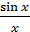обращается в ноль.

Спектр на выходе ИФНЧ:

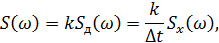
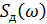– спектр дискретизированного сигнала,

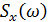– спектр входного воздействия,

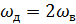– частота дискретизации.

Рисунок 3.4. Импульсная характеристика ИФНЧ

Сущность восстановления исходного сигнала по отсчетам Котельникова показана на рис. 3.5.

Рисунок 3.5. Процесс восстановления сигнала по отсчетам Котельникова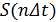

Таким образом, с точностью до постоянного множителя мы получим на выходе ИФНЧ спектр исходного сигнала. С временной точки зрения мы получим исходный непрерывный сигнал .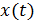

3.2. Погрешности дискретизации и восстановления непрерывных сигналов

Теорема Котельникова справедлива только для сигналов с финитным (ограниченным) спектром. На рис. 3.6 показаны некоторые варианты финитных спектров.

Финитный сигнал:

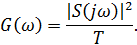
Рисунок 3.6. Пример финитных сигналов (с ограниченным спектром)

Однако спектры реальных информационных сигналов бесконечны. В этом случае Теорема Котельникова справедлива с погрешностью. Погрешность дискретизации определяется энергией спектральных оставляющих сигнала, лежащих за пределами частоты 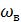(рис. 3.7).

Реальный сигнал:

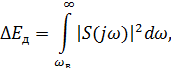
– погрешность дискретизации.

Рисунок 3.7. Спектр сигнала, ограниченного ω_в

Вторая причина возникновения погрешностей – неидеальность восстанавливающего ФНЧ. При этом нарушается ортогональность функции типа 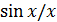и происходит смещение нулей.

Таким образом, погрешность дискретизации и восстановление непрерывного сигнала определяется следующими причинами:

1. Спектры реальных сигналов не финитны;

2. АЧХ идеальных ФНЧ неидеальна.

Пример:

Если в качестве ФНЧ использовать RC-фильтр, то восстановленный сигнал на его выходе будет иметь вид, представленный на рис. 3.8, с учетом того, что импульсная реакция RC-фильтра:

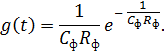
Рисунок 3.8. а) полученный на приеме сигнал;

б) переданный сигнал

Вывод:

Чем выше частота дискретизации 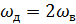и чем ближе спектральная характеристика ФНЧ к идеальной, тем восстановленный сигнал ближе к переданному.

3.3. Структурная схема передачи аналогового сигнала отсчетами Котельникова

На рис. 3.9 изображена структурная схема передачи аналогового сигнала с использованием теоремы Котельникова.

Сообщение от источника преобразовывается в первичный сигнал и поступает на фильтр нижних частот (ФНЧ), который определяет интервал дискретизации 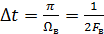, где 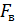– частота среза ФНЧ. Далее в дискретизаторе непрерывная функция преобразуются в дискретные отсчеты, которые с помощью переносчика (модулятора) преобразуются в сигнал, согласованный с линией связи. На приемной стороне после демодулятора отсчеты подаются на ФНЧ и далее сообщение поступает к получателю.

Рисунок 3.9. Структурная схема передачи аналогового сигнала отсчетами Котельникова

Временные и спектральные характеристики сигналов в различных точках структурной схемы показаны на рис. 3.10, 3.11.

Рисунок 3.10. Временные и спектральные характеристики сигналов на передающей стороне

Рисунок 3.11. Временные и спектральные характеристики сигналов на приемной стороне ( 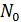– спектральная плотность мощности флуктуационной помехи)

4. Методы формирования и преобразования сигналов

4.1. Классификация радиотехнических цепей

Любая радиотехническая (электрическая) цепь описывается дифференциальным уравнением

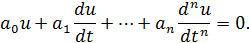
Если 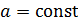, то это линейная электрическая (радиотехническая) цепь (ЛЭЦ). Она состоит из линейных элементов , , .

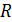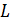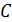Рисунок 4.1. Линейные элементы (ЛЭ)

Для линейной цепи справедлив принцип суперпозиции: реакция на суммарное воздействие равна сумме реакций на каждое из воздействий в отдельности.

Например:

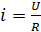– характеристика ЛЭЦ.

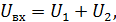
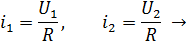
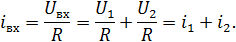
В линейной цепи невозможно появление новых частот, не содержащихся во входном воздействии (сигнале).

1. Если

,

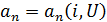то цепь называется нелинейной (НЭЦ) и состоит из нелинейных , , .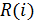

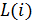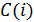Рисунок 4.2. Нелинейные элементы (НЭ)

Для НЭЦ не справедлив принцип суперпозиции. Пусть НЭЦ описывается уравнением:

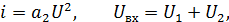
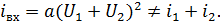
В НЭЦ возникают новые частоты, не содержащиеся во входном воздействии.

2. Если

,

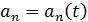то цепь называется параметрической (ПЭЦ) и состоит из элементов, зависящих от времени:

Рисунок 4.3. Параметрические элементы (ПЭ)

Для ПЭЦ:

а) справедлив принцип суперпозиции;

б) возможно появление новых частот.

ПЭЦ конструируется на основе нелинейных элементов, на которые мы подаем напряжение независящее от времени.

Рисунок 4.4. Пример использования параметрического элемента

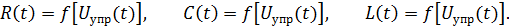
Принципы преобразования спектров

Рисунок 4.5. Использование ПЭ (НЭ)

Таблица 1 – Характеристики сигналов

На входе НЭ (ПЭ)	На выходе НЭ (ПЭ)
Спектр воздействия: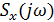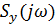
Функция плотности вероятностей: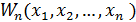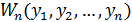
Функция распределения вероятностей: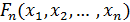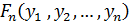
Математическое ожидание: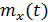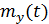
Дисперсия: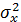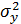
Функция корреляции: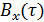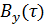
Интервал корреляции: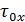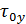
Коэффициент корреляции: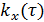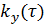
Энергетический спектр: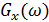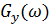
Полоса спектра: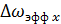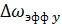

Преобразования бывают:

Пассивные преобразования – такое преобразование, в результате которого не возникает новых частот.

Активные преобразования – такое преобразование, в результате которого возникают новые частоты (которых не было в исходном возмущении). Активное преобразование возможно только с использованием нелинейного или параметрического элемента (т.е. возможно только в нелинейных или параметрических цепях).

Рассмотрим нелинейную цепь:

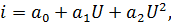
где 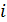– параметр цепи,

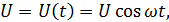
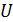– возмущение (воздействие),

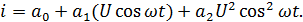
Т.к.

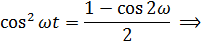
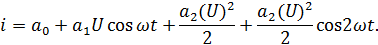
Амплитуда 1-й Постоянная Амплитуда 2-ой

гармоники составляющая гармоники

Иногда появление новых частот является вредным явлением, например, при усилении НЧ сигналов, что приводит к нелинейным искажениям.

Относительный уровень нелинейных искажений определяется коэффициентом гармоник и рассчитывается по формуле:

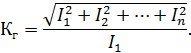
Рисунок 4.6. Спектры токов на входе и выходе НЭ

Рассмотрим воздействие бигармонического колебания на нелинейный элемент:

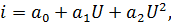
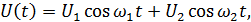
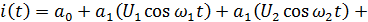
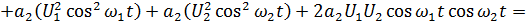
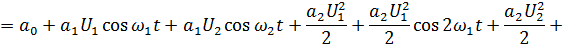
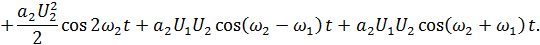
Рисунок 4.7. Спектры напряжений (токов) при воздействии бигармонического колебания на НЭ

Для параметрической цепи:

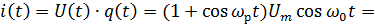
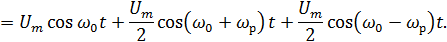
При преобразованиях кроме нелинейных элементов используются фильтры, т.е. линейные элементы.

4.2. Виды преобразования спектров сигнала

1. Умножение частоты – умножение частоты в целое число раз по отношению к частоте входного сигнала.

Рисунок 4.8. Пример умножения частоты на 3

Рисунок 4.9. Функциональные схемы умножителей частоты:

а) на диоде;

б) на транзисторе

2. Деление частоты – получение частоты в 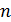раз меньше, чем частота входного сигнала.

3. Преобразование частоты – суммарно-разностные частоты, получаемые при преобразовании частоты из частот входного сигнала и некоторой частоты вспомогательного сигнала.

Рисунок 4.10. Функциональная схема преобразователя частоты

Рисунок 4.11. Пример преобразования частоты «вверх»

4. Модуляция.

В технике связи сигналы на большие расстояния предаются с помощью модуляции (с использованием для этой цели вспомогательного переносчика) т.е. вспомогательного несущего колебания. При модуляции, как и при преобразовании частоты, происходит перенос низкочастотного (НЧ) спектра в область высоких частот (ВЧ).

Примечание: модулированные колебания меньше искажаются в канале связи, чем НЧ сигналы, т.к. НЧ относительно широкополосные, а модулированные – узкополосные. Таким образом:

1) можно бороться с искажением;

2) при использовании вспомогательного несущего колебания можно осуществлять частотную селекцию, которая используется в многоканальных системах связи, т.к. такие сигналы можно разделять с помощью фильтров.

Модуляция – управление одним (или несколькими) из параметров несущего колебания по закону НЧ сигнала.

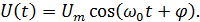
АМ ЧМ ФМ

5. Детектирование – это процесс, обратный процессу модуляции.

При детектировании выявляется, по какому закону промодулирован сигнал.

4.3. Амплитудно-модулированные сигналы

При амплитудной модуляции амплитуда высокочастотного (ВЧ) сигнала изменяется по закону передаваемого низкочастотного (НЧ) сигнала.

При модуляции гармоническим колебанием:

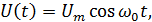
где 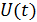– несущее колебание,

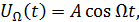
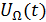– модулирующее колебание.

При АМ:

.

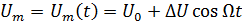Если 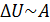,то:

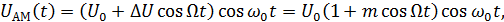
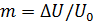– коэффициент глубины модуляции,

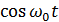– несущее ВЧ колебание,

,

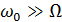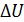– амплитуда огибающей,

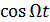– модулирующее НЧ колебание.

Рисунок 4.12. а) модулирующее колебание;

б) модулированное колебание

Рисунок 4.13. Временные характеристики АМ-колебания при различных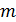

Если модулирующий сигнал более сложной формы (не гармоническое колебание):

Рисунок 4.14. Временные характеристики:

а) модулирующего колебания сложной формы;

б) АМ-колебания

Огибающая изменяется в соответствии с формой модулирующего сигнала.

4.4. Дискретная амплитудная модуляция (ДАМ)

Модулирующее колебание может быть не только непрерывным, но и дискретным. На рис. 4.14 приведен пример модуляции дискретным сигналом.

Рисунок 4.15. Пример ДАМ

Таким образом, под АМ понимается изменение амплитуды ВЧ сигнала переносчика, по закону передаваемого НЧ сигнала.

4.5. Спектральное и векторное представление амплитудно-модулированного сигнала

Спектральное представление:

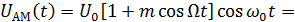
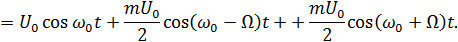
Рисунок 4.16. Спектральное представление АМ-сигнала при модуляции чистым тоном

Ширина спектра АМ сигнала в 2 раза шире спектра передаваемого (модулирующего) сигнала.

4.6. Определение глубины модуляции по спектральной диаграмме (графический метод)

,

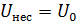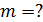
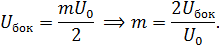
Векторное представление:

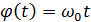– фаза колебания (пройденный путь),

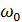– угловая скорость частоты.

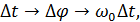
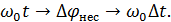
Рисунок 4.17. Векторная диаграмма АМ-колебания

Принято при изображении модулированного колебания вектор несущей 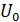считать неподвижным, а векторы боковых выражаются относительно концов несущей.

Рисунок 4.18. Векторное представление АМ-колебания в различные моменты времени ( , , )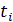

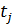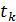Вывод:

Аналитическое, спектральное и векторное предс