Полуклассическая квантовая механика
Трудности классической
Статистической физики
На рубеже XIX–XX вв. делались попытки применить классическую статистическую физику для описания электромагнитного теплового излучения в полости и электронного газа в металле. Оказалось, что в этих областях ее следствия противоречат опыту. Рассмотрим два примера.
Теплоемкость твердых тел
Металл состоит из кристаллической решетки ионов, потерявших свои валентные электроны, и электронов, ставших свободными. Для одновалентного металла количество ионов равно количеству свободных электронов и для моля вещества равно числу Авогадро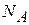 
. Теплоемкость складывается из теплоемкости электронного газа 
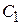и теплоемкости ионов решетки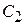 
.
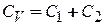Свободный электрон имеет 3 степени свободы и по теореме о распределении энергии по степеням свободы его средняя энергия
.
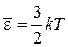Внутренняя энергия моля
,
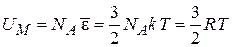молярная теплоемкость электронного газа
.
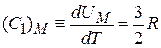Ион решетки имеет 3 колебательные степени свободы, на каждую приходится тепловая энергия kT, тогда средняя энергия иона и внутренняя энергия моля:
,
.
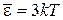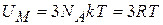В результате молярная теплоемкость кристаллической решетки
.
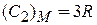Для молярной теплоемкости металла получаем
,
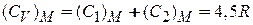для диэлектрика, не имеющего свободных электронов:
.
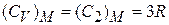Эксперименты при нормальной и более высокой температурах подтверждают закон Дюлонга и Пти (П.4.3)
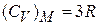
как для металлов, так и для диэлектриков. Следовательно, электронный газ не дает вклада в теплоемкость металла.
При температуре, существенно меньшей нормальной, эксперимент обнаруживает зависимость теплоемкости от температуры:
для диэлектриков
,
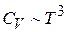для металлов
.
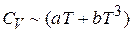Объяснить эти результаты классическая теория не в состоянии, необходимо учитывать квантовые свойства микрочастиц.
Магнетизм системы зарядов
Нильс Бор и Хендрик ван Лёвендоказали, что система зарядов, подчиняющаяся классической физике, не проявляет магнитных свойств, что противоречит известным свойствам магнетизма ряда металлов.
Требуется очертить рамки, в пределах которых можно доверять классической физике. Для этого рассмотрим основные положения квантовой механики. Когда они несущественны, тогда применима классическая физика.
Квантовые свойства
Квантовые свойства проявляет любая система при определенных значениях своих параметров. Например, полупроводниковые гетероструктуры микроскопического размера в виде потенциальных ям, квантовых нитей, точек, периодических структур, через которые распространяются микрочастицы – электроны, дырки, квазичастицы, имеют свойства, парадоксальные с точки зрения классической физики:
– общее сопротивление последовательно соединенных элементов не равно сумме сопротивлений;
– частица проходит через барьер, превышающий ее энергию;
– воздействие на частицу системы в перепутанном состоянии мгновенно влияет на другие частицы системы, на каком бы расстоянии они не находились;
– частица движется одновременно разными путями.
Квантовая механика объясняет явления, которые вызвали трудности у классической физики, и открывает новые технические возможности. Использование квантовых режимов работы приборов микро- и наноэлектроники делает квантовую механику инженерной дисциплиной. По данным 2003 г. около 30% национального продукта США базируется на изобретениях, ставших возможными благодаря квантовой механике.
ПОЛУКЛАССИЧЕСКАЯ КВАНТОВАЯ МЕХАНИКА
Исследования, выполненные на рубеже ХIX–ХХ вв., доказали, что свет и вещество проявляют аналогичные свойства. Это стало основой для создания полуклассической квантовой механики, описывающей частицы вещества.
Свет проявляет корпускулярно-волновую двойственность – в зависимости от длины волны и особенностей экспериментальной установки обнаруживаются волновые или корпускулярные свойства.
Волновые свойства света
Свет – электромагнитная волна. Магнитная составляющая волны не влияет на заряды, движущиеся со скоростями, гораздо меньшими скорости света. Если поляризация несущественна, то электрическая составляющая плоской гармонической волны, распространяющейся вдоль оси x, имеет вид
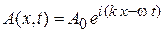, (1.1)
где
А0 – амплитуда;
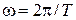– круговая частота, Т – период колебаний;
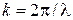– волновое число, λ – длина волны.
Плотность энергии волны определяется как усредненная по времени энергия единицы объема
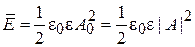. (1.2)
Интерференция
При наложении согласованных по фазе волн происходит перераспределение энергии в пространстве.
Если гармоническая волна разделяется на две волны с равными амплитудами, которые проходят пути x1 и x2 до области наложения волн, то амплитуда суммарного колебания зависит от разности хода
.
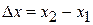Максимум интерференции – смещения в складывающихся волнах 1 и 2 происходят в фазе, результирующая амплитуда удваивается, плотность энергии (1.2) учетверяется.
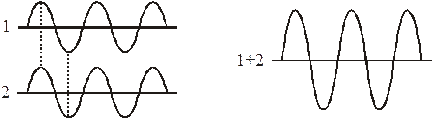
Разность хода кратна длине волны
, 
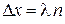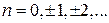(1.3)
Минимум интерференции – складывающиеся волны колеблются в противофазе и гасят друг друга, результирующая амплитуда и плотность энергии равны нулю.
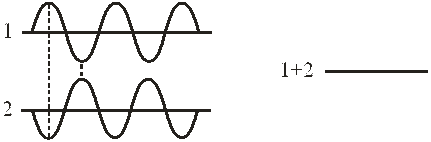
Разность хода кратна нечетному числу полуволн
,
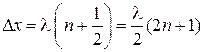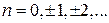
При малой длине волны по сравнению с разностью хода
, 
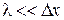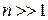
максимумы и минимумы сливаются, результат усредняется, интерференция не проявляется, и свет описывается геометрической оптикой.
Дифракция
Волна отклоняется от прямолинейного распространения при ограничении ее волновой поверхности.
Рассмотрим экран со щелью шириной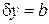 
, на который по оси x падает плоская волна. До экрана волновая поверхность неограничена в плоскости перпендикулярной оси x. Проекции волнового вектора и неопределенности положения и волнового вектора по оси y равны
,
, 
,
.
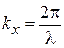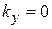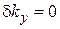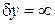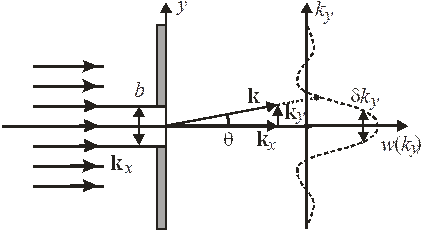
Щель ограничивает проходящую волновую поверхность. После щели амплитуда волны вдоль оси y описывается прямоугольной функцией
.
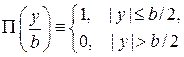Распределение прошедшей волны по поперечному волновому числу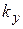 
является Фурье-образом волны
.
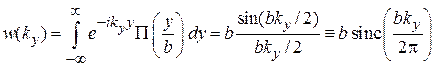Распределение показано на рисунке пунктиром. Максимум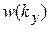 
расположен при 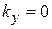. Вне области шириной
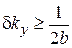
спектр составляет менее сотой доли от максимального значения.
Следовательно, из-за ограничения волновой поверхности интервалом
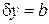
волна отклоняется от первоначального направления, т. е. дифрагирует, в пределах характерного угла
.
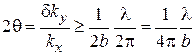Чем уже щель, тем сильнее дифракция.
При малой длине волны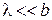 
получаем 
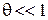, дифракция несущественна, свет описывается геометрической оптикой и проявляет корпускулярные свойства.