Наше представление о Вселенной 4 страница

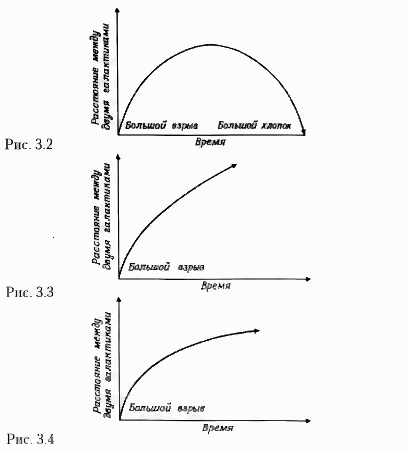
Сам Фридман рассматривал только одну модель, но можно указать три разные модели, для которых выполняются оба фундаментальных предположения Фридмана. В модели первого типа (открытой самим Фридманом) Вселенная расширяется достаточно медленно для того, чтобы в силу гравитационного притяжения между различными галактиками расширение Вселенной замедлялось и в конце концов прекращалось. После этого галактики начинают приближаться друг к другу, и Вселенная начинает сжиматься. На рис. 3.2 показано, как меняется со временем расстояние между двумя соседними галактиками. Оно возрастает от нуля до некоего максимума, а потом опять падает до нуля. В модели второго типа расширение Вселенной происходит так быстро, что гравитационное притяжение хоть и замедляет расширение, не может его остановить. На рис. 3.3 показано, как изменяется в этой модели расстояние между галактиками. Кривая выходит из нуля, а в конце концов галактики удаляются друг от друга с постоянной скоростью. Есть, наконец, и модель третьего типа, в которой скорость расширения Вселенной только‑только достаточна для того, чтобы избежать сжатия до нуля (коллапса). В этом случае расстояние между галактиками тоже сначала равно нулю (рис. 3.4), а потом все время возрастает. Правда, галактики «разбегаются» все с меньшей и меньшей скоростью, но она никогда не падает до нуля.

Модель Фридмана первого типа удивительна тем, что в ней Вселенная не бесконечна в пространстве, хотя пространство не имеет границ. Гравитация настолько сильна, что пространство, искривляясь, замыкается с самим собой, уподобляясь земной поверхности. Ведь, перемещаясь в определенном направлении по поверхности Земли, вы никогда не натолкнетесь на абсолютно непреодолимую преграду, не вывалитесь через край и в конце концов вернетесь в ту же самую точку, откуда вышли. В первой модели Фридмана пространство такое же, но только вместо двух измерений, поверхность Земли имеет три измерения. Четвертое измерение, время, тоже имеет конечную протяженность, но оно подобно отрезку прямой, имеющему начало и конец. Потом мы увидим, что если общую теорию относительности объединить с квантово‑механическим принципом неопределенности, то окажется, что и пространство, и время могут быть конечными, не имея при этом ни краев, ни границ.

Мысль о том, что можно обойти вокруг Вселенной и вернуться в то же место, годится для научной фантастики, но не имеет практического значения, ибо, как можно показать, Вселенная успеет сжаться до нуля до окончания обхода. Чтобы вернуться в исходную точку до наступления конца Вселенной, пришлось бы передвигаться со скоростью, превышающей скорость света, а это невозможно!

В первой модели Фридмана (в которой Вселенная расширяется и сжимается) пространство искривляется, замыкаясь само на себя, как поверхность Земли. Поэтому размеры его конечны. Во второй же модели, в которой Вселенная расширяется бесконечно, пространство искривлено иначе, как поверхность седла. Таким образом, во втором случае пространство бесконечно. Наконец, в третьей модели Фридмана (с критической скоростью расширения) пространство плоское (и, следовательно, тоже бесконечное).

Но какая же из моделей Фридмана годится для нашей Вселенной? Перестанет ли Вселенная наконец расширяться и начнет сжиматься или же будет расширяться вечно? Чтобы ответить на этот вопрос, нужно знать нынешнюю скорость расширения Вселенной и ее среднюю плотность. Если плотность меньше некоторого критического значения, зависящего от скорости расширения, то гравитационное притяжение будет слишком мало, чтобы остановить расширение. Если же плотность больше критической, то в какой‑то момент в будущем из‑за гравитации расширение Вселенной прекратится и начнется сжатие.

Сегодняшнюю скорость расширения Вселенной можно определить, измеряя (по эффекту Доплера) скорости удаления от нас других галактик. Такие измерения можно выполнить очень точно. Но расстояния до других галактик нам плохо известны, потому что их нельзя измерить непосредственно. Мы знаем лишь, что Вселенная расширяется за каждую тысячу миллионов лет на 5‑10%. Однако неопределенность в современном значении средней плотности Вселенной еще больше. Если сложить массы всех наблюдаемых звезд в нашей и других галактиках, то даже при самой низкой оценке скорости расширения сумма окажется меньше одной сотой той плотности, которая необходима для того, чтобы расширение Вселенной прекратилось. Однако и в нашей, и в других галактиках должно быть много темной материи, которую нельзя видеть непосредственно, но о существовании которой мы узнаем по тому, как ее гравитационное притяжение влияет на орбиты звезд в галактиках. Кроме того, галактики в основном наблюдаются в виде скоплений, и мы можем аналогичным образом сделать вывод о наличии еще большего количества межгалактической темной материи внутри этих скоплений, влияющего на движение галактик. Сложив массу всей темной материи, мы получим лишь одну десятую того количества, которое необходимо для прекращения расширения. Но нельзя исключить возможность существования и какой‑то другой формы материи, распределенной равномерно по всей Вселенной и еще не зарегистрированной, которая могла бы довести среднюю плотность Вселенной до критического значения, необходимого, чтобы остановить расширение. Таким образом, имеющиеся данные говорят о том, что Вселенная, вероятно, будет расширяться вечно. Единственное, в чем можно быть совершенно уверенным, так это в том, что если сжатие Вселенной все‑таки произойдет, то никак не раньше, чем через десять тысяч миллионов лет, ибо по крайней мере столько времени она уже расширяется. Но это не должно нас слишком сильно тревожить: к тому времени, если мы не переселимся за пределы Солнечной системы, человечества давно уже не будет – оно угаснет вместе с Солнцем!

Все варианты модели Фридмана имеют то общее, что в какой‑то момент времени в прошлом (десять‑двадцать тысяч миллионов лет назад) расстояние между соседними галактиками должно было равняться нулю. В этот момент, который называется большим взрывом, плотность Вселенной и кривизна пространства‑времени должны были быть бесконечными.

Поскольку математики реально не умеют обращаться с бесконечно большими величинами, это означает, что, согласно общей теории относительности (на которой основаны решения Фридмана), во Вселенной должна быть точка, в которой сама эта теория неприменима. Такая точка в математике называется особой (сингулярной). Все наши научные теории основаны на предположении, что пространство‑время гладкое и почти плоское, а потому все эти теории неверны в сингулярной точке большого взрыва, в которой кривизна пространства‑времени бесконечна. Следовательно, даже если бы перед большим взрывом происходили какие‑нибудь события, по ним нельзя было бы спрогнозировать будущее, так как в точке большого взрыва возможности предсказания свелись бы к нулю. Точно так же, зная только то, что произошло после большого взрыва (а мы знаем только это), мы не сможем узнать, что происходило до него. События, которые произошли до большого взрыва, не могут иметь никаких последствий, касающихся нас, и поэтому не должны фигурировать в научной модели Вселенной. Следовательно, нужно исключить их из модели и считать началом отсчета времени момент большого взрыва.

Мысль о том, что у времени было начало, многим не нравится, возможно, тем, что в ней есть намек на вмешательство божественных сил. (В то же время за модель большого взрыва ухватилась Католическая Церковь и в 1951 г. официально провозгласила, что модель большого взрыва согласуется с Библией). В связи с этим известно несколько попыток обойтись без большого взрыва. Наибольшую поддержку получила модель стационарной Вселенной. Ее авторами в 1948 г. были X. Бонди и Т. Гоулд, бежавшие из оккупированной нацистами Австрии, и англичанин Ф. Хойл, который во время войны работал с ними над проблемой радиолокации. Их идея состояла в том, что по мере разбегания галактик на освободившихся местах из нового непрерывно рождающегося вещества все время образуются новые галактики. Следовательно, Вселенная должна выглядеть примерно одинаково во все моменты времени и во всех точках пространства. Конечно, для непрерывного «творения» вещества требовалась некоторая модификация теории относительности, но нужная скорость творения оказывалась столь малой (одна частица на кубический километр в год), что не возникало никаких противоречий с экспериментом. Стационарная модель – это пример хорошей научной теории в смысле критериев главы 1: она простая и дает определенные предсказания, которые можно проверять путем наблюдений. Одно из ее предсказаний таково: должно быть постоянным число галактик и других аналогичных объектов в любом заданном объеме пространства независимо от того, когда и где во Вселенной производятся наблюдения. В конце 50‑х‑начале 60‑х годов астрономы из Кембриджского университета под руководством М. Райла (который во время войны вместе с Бонди, Гоулдом и Хойлом тоже занимался разработкой радиолокации) составили каталог источников радиоволн, приходящих из внешнего пространства. Эта кембриджская группа показала, что большая часть этих радиоисточников должна находиться вне нашей Галактики (многие источники можно было отождествить даже с другими галактиками) и, кроме того, что слабых источников гораздо больше, чем сильных. Слабые источники интерпретировались как более удаленные, а сильные – как те, что находятся ближе. Далее, оказалось, что число обычных источников в единице объема в удаленных областях больше, чем вблизи. Это могло означать, что мы находимся в центре огромной области Вселенной, в которой меньше источников, чем в других местах. Но, возможно, было и другое объяснение: в прошлом, когда радиоволны начали свой путь к нам, источников было больше, чем сейчас. Оба эти объяснения противоречат предсказаниям теории стационарной Вселенной. Кроме того, микроволновое излучение, обнаруженное в 1965 г. Пензиасом и Вильсоном, тоже указывало на большую плотность Вселенной в прошлом, и поэтому от модели стационарной Вселенной пришлось отказаться.

В 1963 г. два советских физика, Е. М. Лифшиц и И. М. Халатников, сделали еще одну попытку исключить большой взрыв, а с ним и начало времени. Лифшиц и Халатников высказали предположение, что большой взрыв – особенность лишь моделей Фридмана, которые в конце концов дают лишь приближенное описание реальной Вселенной. Не исключено, что из всех моделей, в какой‑то мере описывающих существующую Вселенную, сингулярность в точке большого взрыва возникает только в моделях Фридмана. Согласно Фридману, все галактики удаляются в прямом направлении друг от друга, и поэтому все они находились в одном месте. Однако в реально существующей Вселенной галактики никогда не расходятся точно по прямой: обычно у них есть еще и небольшие составляющие скорости, направленные под углом. Поэтому на самом деле галактикам не нужно находиться точно в одном месте – достаточно, чтобы они были расположены очень близко друг к другу. Тогда нынешняя расширяющаяся Вселенная могла возникнуть не в сингулярной точке большого взрыва, а на какой‑нибудь более ранней фазе сжатия; может быть, при сжатии Вселенной столкнулись друг с другом не все частицы. Какая‑то доля их могла пролететь мимо друг друга и снова разойтись в разные стороны, в результате чего и происходит наблюдаемое сейчас расширение Вселенной. Как тогда определить, был ли началом Вселенной большой взрыв? Лифшиц и Халатников занялись изучением моделей, которые в общих чертах были бы похожи на модели Фридмана, но отличались от фридмановских тем, что в них учитывались нерегулярности и случайный характер реальных скоростей галактик во Вселенной. В результате Лифшиц и Халатников показали, что в таких моделях большой взрыв мог быть началом Вселенной даже в том случае, если галактики не всегда разбегаются по прямой, по это могло выполняться лишь для очень ограниченного круга моделей, в которых движение галактик происходит определенным образом. Поскольку же моделей фридмановского типа, не содержащих большой взрыв, бесконечно больше, чем тех, которые содержат такую сингулярность, Лифшиц и Халатников утверждали, что на самом деле большого взрыва не было. Однако позднее они нашли гораздо более общий класс моделей фридмановского типа, которые содержат сингулярности и в которых вовсе не требуется, чтобы галактики двигались каким‑то особым образом. Поэтому в 1970 г. Лифшиц и Халатников отказались от своей теории.

Тем не менее их работа имела очень важное значение, ибо показала, что если верна общая теория относительности, то Вселенная могла иметь особую точку, большой взрыв. Но эта работа не давала ответа на главный вопрос: следует ли из общей теории относительности, что у Вселенной должно было быть начало времени – большой взрыв? Ответ на этот вопрос был получен при совершенно другом подходе, предложенном в 1965 г. английским математиком и физиком Роджером Пенроузом. Исходя из поведения световых конусов в общей теории относительности и того, что гравитационные силы всегда являются силами притяжения, Пенроуз показал, что когда звезда сжимается под действием собственных сил гравитации, она ограничивается областью, поверхность которой в конце концов сжимается до нуля. А раз поверхность этой области сжимается до нуля, то же самое должно происходить и с ее объемом. Все вещество звезды будет сжато в нулевом объеме, так что ее плотность и кривизна пространства‑времени станут бесконечными. Иными словами, возникнет сингулярность в некоей области пространства‑времени, называемая черной дырой.

На первый взгляд, эта теорема Пенроуза относится только к звездам: в ней ничего не говорится о том, испытала ли вся Вселенная в прошлом большой взрыв. В то время, когда Пепроуз доказал свою теорему, я, будучи аспирантом, отчаянно искал какую‑нибудь задачу, чтобы защитить диссертацию. За два года до этого врачи поставили мне диагноз «боковой амиотрофическнй склероз», или моторная болезнь нейронов, и дали понять, что я протяну не больше одного‑двух лет. При таких обстоятельствах не было особого смысла работать над диссертацией, ибо я не надеялся дожить до ее завершения. Но прошло два года, а хуже мне не стало. Мои дела шли прекрасно, и я был помолвлен с очаровательной девушкой по имени Джейн Уайлд. Для женитьбы мне требовалась работа, а чтобы ее получить, нужна была докторская степень.

В 1965 г. я прочитал о теореме Пенроуза, согласно которой любое тело в процессе гравитационного коллапса должно в конце концов сжаться в сингулярную точку. Вскоре я понял, что если в теореме Пенроуза изменить направление времени на обратное, так, чтобы сжатие перешло в расширение, то эта теорема тоже будет верна, коль скоро Вселенная сейчас хотя бы грубо приближенно описывается в крупном масштабе моделью Фридмана. По теореме Пенроуза конечным состоянием любой коллапсируюшей звезды должна быть сингулярность; при обращении времени эта теорема утверждает, что в любой модели фридмановского типа начальным состоянием расширяющейся Вселенной тоже должна быть сингулярность. По соображениям технического характера в теорему Пенроуза было введено в качестве условия требование, чтобы Вселенная была бесконечна в пространстве. Поэтому на основании этой теоремы я мог доказать лишь, что сингулярность должна существовать, если расширение Вселенной происходит достаточно быстро, чтобы не началось повторное сжатие (ибо только такие фридмановские модели бесконечны в пространстве).

Потом я несколько лет разрабатывал новый математический аппарат, который позволил бы устранить это и другие технические условия из теоремы о необходимости сингулярности. В итоге в 1970 г. мы с Пенроузом написали совместную статью, в которой наконец доказали, что сингулярная точка большого взрыва должна существовать, опираясь только на то, что верна общая теория относительности и что во Вселенной содержится столько вещества, сколько мы видим. Наша работа вызвала массу возражений, частично со стороны советских ученых, которые из‑за приверженности марксистской философии верили в научный детерминизм, а частично и со стороны тех, кто не принимал саму идею сингулярностей как нарушающую красоту теории Эйнштейна. Но с математической теоремой не очень поспоришь, и поэтому, когда работа была закончена, ее приняли, и сейчас почти все считают, что Вселенная возникла в особой точке большого взрыва. По иронии судьбы мои представления изменились, и теперь я пытаюсь убедить физиков в том, что на самом деле при зарождении Вселенной никакой особой точки не было. В следующих главах я покажу, что при учете квантовых эффектов сингулярность может исчезнуть.

В этой главе мы видели, как менее чем за полстолетия изменились представления людей о природе, формировавшиеся не одну тысячу лет. Начало этим изменениям положили открытое Хабблом расширение Вселенной и сознание незначительности нашей собственной планеты среди огромных просторов Вселенной. По мере того как множились экспериментальные и теоретические результаты, становилось все более ясно, что у Вселенной должно быть начало во времени. Наконец в 1970 г. мы с Пенроузом доказали это, исходя из общей теории относительности Эйнштейна. Из нашего доказательства следовало, что общая теория относительности представляет собой неполную теорию; в ней нет ответа на вопрос, как возникла Вселенная, потому что, согласно теории относительности, все физические теории, в их числе и она сама, нарушаются в точке возникновения Вселенной. Однако общая теория относительности и не претендует на роль полной теории: теоремы о сингулярности на самом деле утверждают лишь, что на некоей очень ранней стадии развития размеры Вселенной были очень малы, настолько, что тогда могли быть весьма существенными мелкомасштабные эффекты, которыми занимается уже другая величайшая теория XX века – квантовая механика. Итак, в начале 70‑х годов нам пришлось в своих исследованиях Вселенной переключиться с теории чрезвычайно большого на теорию крайне малого. Этой теории, квантовой механике, будет посвящена следующая глава, а затем мы перейдем к обсуждению того, как эти две частные теории можно было бы объединить в единую квантовую теорию гравитации.

Принцип неопределенности

Под влиянием успеха научных теорий, особенно ньютоновской теории тяготения, у французского ученого Пьера Лапласа в начале XIX в. выработался взгляд на Вселенную как на полностью детерминированный объект. Лаплас полагал, что должен существовать набор научных законов, которые позволяли бы предсказать все, что может произойти во Вселенной, если только известно полное описание ее состояния в какой‑то момент времени. Например, если бы мы знали положения Солнца и планет, отвечающие какому‑то моменту времени, то с помощью законов Ньютона мы могли бы вычислить, в каком состоянии оказалась бы Солнечная система в любой другой момент времени. В данном случае детерминизм довольно очевиден, но Лаплас пошел дальше, утверждая, что существуют аналогичные законы для всего, в том числе и для поведения человека.

Доктрина научного детерминизма встретила сильное сопротивление со стороны многих, почувствовавших, что этим ограничивается свободное вмешательство Бога в наш мир; тем не менее эта идея оставалась обычной научной гипотезой еще в самом начале нашего века. Одним из первых указаний на необходимость отказа от детерминизма стали результаты расчетов двух английских физиков, Джона Рэлея и Джеймса Джинса, из которых следовало, что горячий объект типа звезды должен все время излучать бесконечно большую энергию. Согласно известным тогда законам, горячее тело должно в равной мере излучать электромагнитные волны всех частот (например, радиоволны, видимый свет, рентгеновское излучение). Это означает, что должно излучаться одинаковое количество энергии и в виде волн с частотами от одного до двух миллионов миллионов волн в секунду, и в виде волн, частоты которых находятся в интервале от двух до трех миллионов миллионов волн в секунду. А поскольку разных частот бесконечно много, полная излучаемая энергия должна быть бесконечной.

Чтобы избавиться от этого явно абсурдного вывода, немецкий ученый Макс Планк в 1900 г. принял гипотезу, согласно которой свет, рентгеновские лучи и другие волны не могут испускаться с произвольной интенсивностью, а должны испускаться только некими порциями, которые Планк назвал квантами. Кроме того, Планк предположил, что каждый квант излучения несет определенное количество энергии, которое тем больше, чем выше частота волн. Таким образом, при достаточно высокой частоте энергия одного кванта может превышать имеющееся количество энергии и, следовательно, высокочастотное излучение окажется подавленным, а интенсивность, с которой тело теряет энергию, будет конечной.

Гипотеза квантов прекрасно согласовалась с наблюдаемыми значениями интенсивности излучения горячих тел, но что она означает для детерминизма, было неясно до 1926 г., когда другой немецкий ученый, Вернер Гейзенберг, сформулировал знаменитый принцип неопределенности. Чтобы предсказать, каким будет положение и скорость частицы, нужно уметь производить точные измерения ее положения и скорости в настоящий момент. Очевидно, что для этого надо направить на частицу свет. Часть световых волн на ней рассеется, и таким образом мы определим положение частицы в пространстве. Однако точность этого измерения будет не выше, чем расстояние между гребнями двух соседних волн, и поэтому для точного измерения положения частицы необходим коротковолновый свет. Согласно же гипотезе Планка, свет невозможно использовать произвольно малыми порциями, и не бывает меньшей порции, чем один квант. Этот квант света внесет возмущение в движение частицы и непредсказуемо изменит ее скорость. Кроме того, чем точнее измеряется положение, тем короче должны быть длины световых волн, а следовательно, тем больше будет энергия одного кванта. Это значит, что возмущение скорости частицы станет больше. Иными словами, чем точнее вы пытаетесь измерить положение частицы, тем менее точными будут измерения ее скорости, и наоборот. Гейзенберг показал, что неопределенность в положении частицы, умноженная на неопределенность в се скорости и на ее массу, не может быть меньше некоторого числа, которое называется сейчас постоянной Планка. Это число не зависит ни от способа, которым измеряется положение или скорость частицы, ни от типа этой частицы, т. е. принцип неопределенности Гейзенберга является фундаментальным, обязательным свойством нашего мира.

Принцип неопределенности имеет далеко идущие следствия, относящиеся к нашему восприятию окружающего мира. Даже по прошествии более пятидесяти лет многие философы так окончательно и не согласились с ними, и эти следствия до сих пор остаются предметом споров. Принцип неопределенности означал конец мечтам Лапласа о научной теории, которая давала бы полностью детерминированную модель Вселенной: в самом деле, как можно точно предсказывать будущее, не умея даже в настоящий момент производить точные измерения состояния Вселенной! Конечно, мы можем себе представлять, что существует некий набор законов, полностью определяющий события для какого‑то сверхъестественного существа, которое способно наблюдать современное состояние Вселенной, никак не возмущая ее. Однако такие модели Вселенной не представляют интереса для нас – простых смертных. Лучше, пожалуй, воспользовавшись тем принципом «экономии», который называется принципом «бритвы Оккама» (У. Оккам /1285‑1349/ – английский философ. Суть принципа «бритвы Оккама»: понятия, не поддающиеся проверке в опыте, должны быть удалены из науки. – прим. ред.) взять и вырезать все положения теории, которые не поддаются наблюдению. Приняв такой подход, Вернер Гейзенберг, Эрвин Шредингер и Поль Дирак в 20‑х годах нашего века пересмотрели механику и пришли к новой теории – квантовой механике, в основу которой был положен принцип неопределенности. В квантовой механике частицы больше не имеют таких определенных и не зависящих друг от друга характеристик, как положение в пространстве и скорость, недоступных для наблюдения. Вместо этого они характеризуются квантовым состоянием, которое представляет собой некую комбинацию положения и скорости.

Квантовая механика, вообще говоря, не предсказывает, что наблюдение должно иметь какой‑то единственный определенный результат. Наоборот, она предсказывает некий ряд разных результатов и дает вероятность каждого из них. Это значит, что, выполнив одно и то же измерение для многих одинаковых систем, начальные состояния которых совпадают, мы бы обнаружили, что в одном числе случаев результат измерения равен А, в другом – Б и т. д. Мы можем предсказать, в скольких примерно случаях результат будет равняться А и Б, но определить результат каждого конкретного измерения невозможно. Таким образом, квантовая механика вносит в науку неизбежный элемент непредсказуемости или случайности. Эйнштейн выступил очень резко против этой концепции, несмотря на ту огромную роль, которую сам сыграл в ее развитии. За огромный вклад в квантовую теорию Эйнштейну была присуждена Нобелевская премия. Но он никогда не мог согласиться с тем, что Вселенной управляет случай. Все чувства Эйнштейна нашли свое выражение в его знаменитом высказывании: «Бог не играет в кости». Однако большинство остальных ученых были склонны принять квантовую механику, потому что она прекрасно согласовалась с экспериментом. Квантовая механика в самом деле является выдающейся теорией и лежит в основе почти всей современной науки и техники. Принципы квантовой механики положены в основу работы полупроводниковых и интегральных схем, которые являются важнейшей частью таких электронных устройств, как телевизоры и электронно‑вычислительные машины. На квантовой механике зиждется современная химия и биология. Единственные области физики, которые пока не используют должным образом квантовую механику, – это теория гравитации и теория крупномасштабной структуры Вселенной.

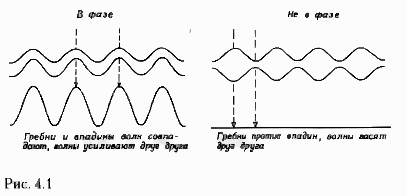
Несмотря на то что световое излучение состоит из волн, тем не менее, согласно гипотезе Планка, свет в каком‑то смысле ведет себя так, как будто он образован частицами: излучение и поглощение света происходит только в виде порций, или квантов. Принцип же неопределенности Гейзенберга говорит о том, что частицы в каком‑то смысле ведут себя как волны: они не имеют определенного положения в пространстве, а «размазаны» по нему с некоторым распределением вероятности. В квантово‑механической теории используется совершенно новый математический аппарат, который уже не описывает сам реальный мир на основе представлений о частицах и волнах; эти понятия можно теперь относить только к результатам наблюдений в этом мире. Таким образом, в квантовой механике возникает частично‑волновой дуализм: в одних случаях частицы удобно считать волнами, а в других лучше считать волны частицами. Из этого следует один важный вывод: мы можем наблюдать так называемую интерференцию между двумя волнами‑частицами. Гребни волн одной из них могут, например, совпадать со впадинами другой. Тогда две волны гасят друг друга, а не усиливают, суммируясь, как можно было бы ожидать, в более высокие волны (рис. 4.1). Всем известный пример интерференции света – переливающиеся разными цветами радуги мыльные пузыри. Это явление возникает в результате отражения света от двух поверхностей тонкой пленки воды, которая образует пузырь. Белый свет содержит всевозможные длины волн, отвечающие разным цветам. Гребни некоторых волн, отраженных от одной из поверхностей мыльной пленки, совпадают со впадинами волн той же длины, отраженных от второй поверхности пузыря. Тогда в отраженном свете будут отсутствовать цвета, соответствующие этим длинам волн, и отраженный свет окажется разноцветным.

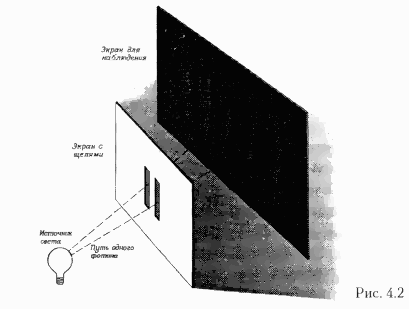
Итак, благодаря возникшему в квантовой механике дуализму частицы тоже могут испытывать интерференцию. Широко известный пример такой интерференции частиц – опыт с двумя щелями в экране (рис. 4.2). Рассмотрим экран, в котором прорезаны две узкие параллельные щели. По одну сторону от экрана со щелями помещен источник света какого‑то определенного цвета (т. е. определенной длины волны). Свет в основном попадает на поверхность экрана, но небольшая его часть пройдет сквозь щели. Далее представим себе экран для наблюдения, установленный по другую от источника света сторону экрана со щелями. Тогда в любую точку экрана для наблюдения будут попадать световые волны из обеих щелей. Но расстояние, пройденное светом через щели от источника до экрана, будет, вообще говоря, разным. Это означает, что волны, прошедшие через щели, попадут на экран в разной фазе: в одних местах они будут ослаблять друг друга, а в других – усиливать. В результате на экране получится характерная картина, составленная из темных и светлых полос.

Удивительно, что в точности такие же полосы возникают при замене источника света источником частиц, скажем, электронов, вылетающих с определенной скоростью (это означает, что им соответствуют волны определенной длины). Описанное явление тем более странно, что при наличии только одной щели никакие полосы не возникают и на экране появляется просто однородное распределение электронов. Можно было бы предположить, что еще одна щель просто увеличит число электронов, попадающих в каждую точку экрана, по на самом деле из‑за интерференции число этих электронов в некоторых местах, наоборот, уменьшается. Если пропускать через щели но одному электрону за раз, то можно было бы ожидать, что каждый из них пройдет либо через одну щель, либо через другую, т. е. будет вести себя так, как будто та щель, через которую он прошел, единственная, и тогда на экране должно возникнуть однородное распределение. Однако на самом деле полосы появляются даже в том случае, когда электроны выпускаются по одному. Следовательно, каждый электрон должен проходить сразу через обе щели!