Розділ 2. Принципи спеціальної теорії відносності. 4 страница
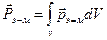 (7.14)
(7.14)
Докладний аналіз (який ми тут опускаємо) показує, що густина імпульсу електромагнітного поля 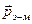 задається виразом:
задається виразом:
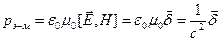 (7.15)
(7.15)
де в останньому з рівностей (7.15) ми скористалися формулою (6.11) для електродинамічної постійної (швидкості поширення електромагнітних хвиль у вакуумі). Формула (7.15) установлює природний зв'язок між густиною імпульсу і густиною потоку енергії електромагнітного поля.
Зауваження 2. Поряд з енергією й імпульсом електромагнітне поле володіє і моментом імпульсу 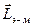 , що виражається через густину моменту імпульсу
, що виражається через густину моменту імпульсу 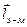 інтегралом:
інтегралом:
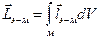 (7.16)
(7.16)
Подібно формулі 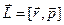 для механічного моменту імпульсу
для механічного моменту імпульсу 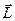 матеріальної точки, що має імпульс,
матеріальної точки, що має імпульс, 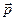 густина моменту імпульсу електромагнітного поля
густина моменту імпульсу електромагнітного поля 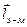 зв'язана з густиною імпульсу поля аналогічною формулою:
зв'язана з густиною імпульсу поля аналогічною формулою:
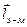 =
= 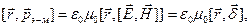 (7.17)
(7.17)
де в останніх двох рівностях ми скористалися виразом (7.15).
Зауваження 3. У цьому §7 ми переконалися, що класичні фізичні поля (електромагнітне, і - за аналогією - гравітаційне) характеризуються тими ж фундаментальними фізичними характеристиками (енергією, імпульсом, моментом імпульсу), що і механічні системи (класична речовина). Це підтверджує єдність двох форм фізичної матерії (речовини і поля) на рівні класичного (неквантового) розгляду. Повна єдність (синтез) у розумінні речовини і поля досягається тільки в квантово-польовій картині світу (у понятті так називаного квантового поля).
Додаток до частини 1
У цьому додатку ми зробимо ряд зауважень про застосування законів електродинаміки вакууму до вивчення електромагнітних явищ у матеріальних середовищах (газах, рідинах, твердих тілах). Єдина мета цього Додатка - показати, яким шляхом з'являються нові характеристики електромагнітного поля 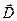 і
і 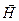 , що були у випадках вакууму формально уведені визначеннями (7.6). Докладні докази результатів, що приводяться, ми тут не приводимо.
, що були у випадках вакууму формально уведені визначеннями (7.6). Докладні докази результатів, що приводяться, ми тут не приводимо.
Застосування законів електродинаміки (5.1) - (5.4) до опису електромагнітних явищ у матеріальних середовищах (у речовині) засновано на наступних основних положеннях класичної електронної теорії Лоренца:
1) матеріальне середовище розглядається як система мікроскопічних зарядів, що рухаються, (наприклад, протонів і електронів);
2) мікроскопічні електромагнітні поля, створювані цими зарядами, описуються рівняннями вакууму (5.1) - (5.4), тобто рівняння мікроскопічної електродинаміки матеріальних середовищ записуються у вигляді:
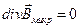 (П.1)
(П.1)
де мікроскопічні характеристики 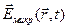 ,
, 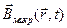 ,
, 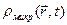 ,
, 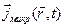 дуже швидко змінюють свої значення як при зміщенні точки спостереження
дуже швидко змінюють свої значення як при зміщенні точки спостереження 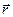 навіть на дуже малі відстані (порядку розмірів атомів), так і при найменшій зміні часу спостереження t (порядку часу протікання атомних процесів). Тому докладний мікроскопічний опис структури електромагнітного поля в речовині є дуже складна задача. На щастя, такий докладний опис найчастіше є і зайвим (наприклад, тіло макроскопічних розмірів не "почуває" флуктуацій поля в межах атома і реагує на електромагнітне поле так, начебто на нього діє поле, усереднене по багатьом атомам). Тому часто застосовують мікроскопічний спосіб опису полів, коли дискретним характером складу речовини зневажають і проводять усереднення всіх характеристик по фізично малому об'ємі і фізично малому проміжку часу. Проводячи таке усереднення рівнянь (П.1), одержуємо систему рівнянь макроскопічної електродинаміки:
навіть на дуже малі відстані (порядку розмірів атомів), так і при найменшій зміні часу спостереження t (порядку часу протікання атомних процесів). Тому докладний мікроскопічний опис структури електромагнітного поля в речовині є дуже складна задача. На щастя, такий докладний опис найчастіше є і зайвим (наприклад, тіло макроскопічних розмірів не "почуває" флуктуацій поля в межах атома і реагує на електромагнітне поле так, начебто на нього діє поле, усереднене по багатьом атомам). Тому часто застосовують мікроскопічний спосіб опису полів, коли дискретним характером складу речовини зневажають і проводять усереднення всіх характеристик по фізично малому об'ємі і фізично малому проміжку часу. Проводячи таке усереднення рівнянь (П.1), одержуємо систему рівнянь макроскопічної електродинаміки:
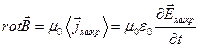 (П.2)
(П.2)
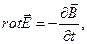 (П.3)
(П.3)
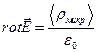 (П.4)
(П.4)
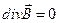 (П.5).
(П.5).
де 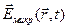 і
і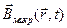 є (на відміну від частини 1) усереднені (мікроскопічні) характеристики поля, а
є (на відміну від частини 1) усереднені (мікроскопічні) характеристики поля, а 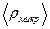 ,
, 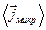 є середні (макроскопічні) значення густини заряду і густини струму.
є середні (макроскопічні) значення густини заряду і густини струму.
З макроскопічної точки зору середню густину заряду 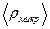 зручно розділити на дві частини:
зручно розділити на дві частини:
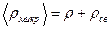 (П.6)
(П.6)
де r – середня густина вільних зарядів (розподіл таких зарядів не залежить від 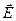 і найчастіше
і найчастіше 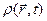 вважається заздалегідь відомою функцією координат і часу), а
вважається заздалегідь відомою функцією координат і часу), а 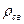 - середня густина зв'язаних зарядів (це заряди атомів і молекул які не можуть переміщатися на мікроскопічні відстані і
- середня густина зв'язаних зарядів (це заряди атомів і молекул які не можуть переміщатися на мікроскопічні відстані і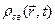 залежить від
залежить від 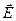 ). Докладний аналіз явищ поляризації середовища показує, що:
). Докладний аналіз явищ поляризації середовища показує, що:
` 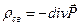 ,(П.7)
,(П.7)
де 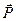 є вектор поляризації середовища (дипольний момент одиниця об'єму середовища).
є вектор поляризації середовища (дипольний момент одиниця об'єму середовища).
Підставляючи (П.6) і (П.7) у рівняння (П.4), перепишемо його вигляді:
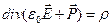 (П.4/)
(П.4/)
чи ,остаточно, у вигляді:
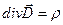 (П.4//)
(П.4//)
де ми ввели нову характеристику електричного поля в матеріальному середовищі - вектор електричної індукції 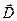 - по визначенню:
- по визначенню:
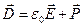 (П.8)
(П.8)
Основною характеристикою електричного поля є його напруженість 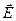 , тому що 1)
, тому що 1) 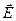 створюється всіма зарядами незалежно від їхньої природи (вільні вони чи зв'язані); 2) сила, що діє на заряд, визначається саме напруженістю електричного поля (див. 2.1). Вектор електричної індукції
створюється всіма зарядами незалежно від їхньої природи (вільні вони чи зв'язані); 2) сила, що діє на заряд, визначається саме напруженістю електричного поля (див. 2.1). Вектор електричної індукції 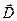 є допоміжна характеристика електричного поля, тому що
є допоміжна характеристика електричного поля, тому що 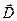 створюється тільки вільними зарядами (див.П.4//). Для безмежних, однорідних середовищ
створюється тільки вільними зарядами (див.П.4//). Для безмежних, однорідних середовищ 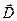 узагалі не залежить від виду середовища, тому що цілком визначається вільними зарядами. Для вакууму з (П.8) випливає
узагалі не залежить від виду середовища, тому що цілком визначається вільними зарядами. Для вакууму з (П.8) випливає 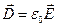 , чим ми і скористалися формально у формулі (7.6).
, чим ми і скористалися формально у формулі (7.6).
Далі з макроскопічної точки зору, у залежності від природи руху зарядів середню густину струму 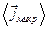 з рівняння (П.2) зручно розділити на три частини:
з рівняння (П.2) зручно розділити на три частини:
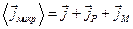 (П.9)
(П.9)
де 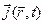 – середня густина струму провідності (у типових випадках провідних середовищ
– середня густина струму провідності (у типових випадках провідних середовищ 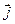 зв'язано з напруженістю електричного поля законом Ома в диференціальній формі:
зв'язано з напруженістю електричного поля законом Ома в диференціальній формі: 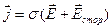 , де
, де 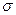 – питома електропровідність середовища, а
– питома електропровідність середовища, а 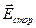 – стороння електрорушійна сила джерел струму, якщо такі маються). Величина
– стороння електрорушійна сила джерел струму, якщо такі маються). Величина 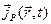 є середня густина поляризаційного струму, зв'язаного з рухом зв'язаних зарядів при поляризації середовища під дією електричного поля; легко показати, що
є середня густина поляризаційного струму, зв'язаного з рухом зв'язаних зарядів при поляризації середовища під дією електричного поля; легко показати, що 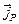 зв'язано з вектором поляризації
зв'язано з вектором поляризації 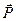 співвідношенням:
співвідношенням:
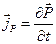 (П.10)
(П.10)
Величина 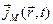 є середня густина струму намагніченості – це середнє значення густини молекулярних струмів. Можна показати, що вектор
є середня густина струму намагніченості – це середнє значення густини молекулярних струмів. Можна показати, що вектор 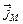 зв'язаний з вектором намагніченості
зв'язаний з вектором намагніченості 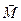 (тобто магнітним моментом одиниця об'єму середовища) співвідношенням:
(тобто магнітним моментом одиниця об'єму середовища) співвідношенням:
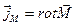 (П.11)
(П.11)
Підставляючи тепер вираження (П.9) - (П.11) у рівняння (П.2) переписуємо останнє у вигляді, чи, після перегруповування доданків, у вигляді:
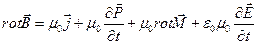
чи, після перегрупування доданків, у вигляді:
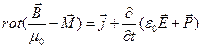 (П.2/)
(П.2/)
Уводячи визначення:

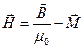
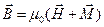 (П.12)
(П.12)
і використовуючи (П.8), переписуємо (П.2/) в остаточному вигляді:
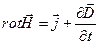 (П.2")
(П.2")
Визначенням (П.12) ми ввели нову характеристику магнітного поля 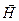 , що називається напруженістю магнітного поля. Магнітна індукція
, що називається напруженістю магнітного поля. Магнітна індукція 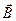 є основною характеристикою магнітного поля тому що 1) породжується рухом зарядів будь-якої природи (як вільних, так і зв'язаних); 2) визначає (відповідно до закону Ампера) силовий вплив магнітного поля на заряди, що рухаються, (струми). Напруженість
є основною характеристикою магнітного поля тому що 1) породжується рухом зарядів будь-якої природи (як вільних, так і зв'язаних); 2) визначає (відповідно до закону Ампера) силовий вплив магнітного поля на заряди, що рухаються, (струми). Напруженість 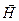 є допоміжною характеристикою магнітного поля, тому що породжується рухом не всіх зарядів, а тільки вільних зарядів (це видно з (П.2")). Вектор
є допоміжною характеристикою магнітного поля, тому що породжується рухом не всіх зарядів, а тільки вільних зарядів (це видно з (П.2")). Вектор 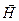 уводиться для спрощення розрахунків при розгляді електромагнітних явищ у матеріальних середовищах. У вакуумі немає молекулярних струмів, тому
уводиться для спрощення розрахунків при розгляді електромагнітних явищ у матеріальних середовищах. У вакуумі немає молекулярних струмів, тому 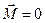 ,і визначення (П.12) для вакууму збігається з формальним визначенням (7.6). Підкреслимо, що при розгляді електромагнітних явищ у вакуумі немає ніякої фізичної причини для використання характеристики
,і визначення (П.12) для вакууму збігається з формальним визначенням (7.6). Підкреслимо, що при розгляді електромагнітних явищ у вакуумі немає ніякої фізичної причини для використання характеристики 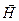 : ми використовували її в §7 чисто формально, тобто тільки для запису результатів у компактній формі.
: ми використовували її в §7 чисто формально, тобто тільки для запису результатів у компактній формі.
Випишемо тепер ще раз систему рівнянь (П.2"), (П.3), (П.4") і (П.5)
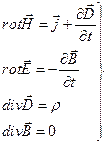 (П.13)
(П.13)
Це є рівняння макроскопічної електродинаміки і називаються рівняннями Максвела. У цьому зв'язку відзначимо , що рівняння макроскопічної електродинаміки (П.10) називається рівняннями Максвела-Лоренца вони мають такий же вигляд, як і рівняння Максвела для електродинаміки вакууму (5.1)-(5.4).
Зауваження 1. Система рівнянь (П.13) не є повною, тобто її недостатньо для визначення всіх характеристик електромагнітного поля в матеріальному середовищі. До цих рівнянь необхідно додати співвідношення між 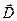 і
і 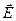 , а також між
, а також між 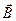 і
і 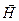 , що задаються формулами (П.8) і (П.12), відповідно. Ці співвідношення називаються матеріальними рівняннями (чи матеріальними умовами). Так як
, що задаються формулами (П.8) і (П.12), відповідно. Ці співвідношення називаються матеріальними рівняннями (чи матеріальними умовами). Так як 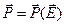 і
і 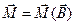 , то завдання матеріальних рівнянь зводиться до завдання явного вигляду функцій
, то завдання матеріальних рівнянь зводиться до завдання явного вигляду функцій 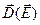 і
і 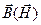 . У найпростішому випадку однорідних і ізотропних середовищ ці функції мають відомий простий вигляд:
. У найпростішому випадку однорідних і ізотропних середовищ ці функції мають відомий простий вигляд:
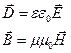 (П.14)
(П.14)
і система рівнянь (П.13) разом з матеріальними умовами (П.14) є повною системою рівнянь макроскопічної електродинаміки однорідних і ізотропних матеріальних середовищ. Однак, для довільних (неоднорідних і анізотропних) середовищ явний вигляд матеріальних рівнянь:
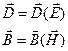 (П.15)
(П.15)
у загальному випадку невідомий, функції (П.15) можуть мати дуже складний вигляд, що залежить від характеру (властивостей) середовища. Тому рівняння (П.15) задаються, як правило, феноменологично, тобто беруться з досвіду.
Зауваження 2. При одержанні фізичних рішень системи рівнянь (П.13) і (П.15) необхідно задати додатково відповідні постійні конкретної задачі –початкові і граничні умови. У багатьох важливих випадках (при наявності граничних поверхонь - границь роздягнула між різними середовищами) такими граничними умовами є співвідношення між нормальними і тангенціальними (стосовно поверхні розподілу) складовими векторів 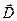 ,
, 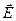 ,
,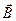 ,
, 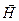 , що легко одержуються (ми їх не приводимо) з відповідної інтегральної форми рівнянь (П.13).
, що легко одержуються (ми їх не приводимо) з відповідної інтегральної форми рівнянь (П.13).
Зауваження 3. Система рівнянь макроскопічної електродинаміки записана тут у системі одиниць СІ. У гауссовой системі одиниць рівняння (П.13) - (П.14) приймають наступний вигляд:
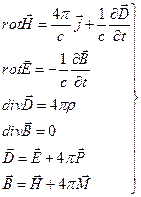 (П.16)
(П.16)
де с - швидкість електромагнітних хвиль у вакуумі .
Зауваження 4. Зробимо одне зауваження методичного характеру. На нашу думку, класичну електродинаміку в педагогічному інституті раціонально викладати в послідовності тем (розділів), зображеної схематично на наступній структурно-логічній схемі:
|

|
|
|
|
|
|
|
|

|




|
|
|
|
|
|

|


Виклад електродинаміки в такій логічній послідовності дозволяє: 1) раціонально сполучити індуктивний (теми I-II ) і дедуктивний (теми III-VII) методи викладу; 2) методологічно правильно освітити зв'язок між електричним і теоретичним рівнем фізичних знань (див. частину 1); 3) акцентувати увагу студентів на основних законах електродинаміки; 4) підкреслити єдність методики застосування рівнянь Максвела до конкретних фізичних задач (теми III - VII); здійснити міжпредметні зв'язки з відповідним розділом курсу загальної фізики (тема I).
Розділ 2. Принципи спеціальної теорії відносності.
Аж до початку XX століття у фізиці панували механістичні уявлення про простір, час, рух (див. частина I, гл. 1), незважаючи на те, що вже була побудована перша фундаментальна теорія (електродинамік Максвела – див. гл. 1) електромагнітної картини світу. Принципово нові уявлення про простір, час, рух виникли тільки в спеціальній теорії відносності (СТВ), побудованої А. Ейнштейном у 1905 році. У СТВ вивчаються високоенергетичні фізичні процеси, зокрема механічний рух тіл з великими швидкостями. При цьому (як і в механіці) дослідження в СТВ проводяться відносно інерціальних систем відліку (ІСВ). Важливо відзначити, що хоча тут ми викладаємо СТВ разом з електродинамікою, однак СТВ є загальфізична теорія, принципи якої відіграють важливу роль і в квантово-польовій картині світу (а не тільки в електромагнітній картині світу). Вивчення ж СТВ разом з електродинамікою доцільно по наступним розуміннях методичного характеру:
1) електродинамічна постійна 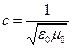 (див. §6) грає в СТВ роль фундаментальної фізичної постійної (саме усвідомлення фундаментальної ролі цієї постійної лежить в основі всіх "парадоксальних" фізичних наслідків СТВ);
(див. §6) грає в СТВ роль фундаментальної фізичної постійної (саме усвідомлення фундаментальної ролі цієї постійної лежить в основі всіх "парадоксальних" фізичних наслідків СТВ);
2) саме електродинаміка є приклад першої релятивістськи інваріантною фізичною теорією (тобто теорією, що задовольняє всім принципам СТВ – див. гл. 3);
3) перші експериментальні обґрунтування СТВ одержали саме в області електромагнітних явищ.
§8. Постулати СТВ. Перетворення Лоренца.
Фундаментальним принципом (постулатом) класичної механіки, у якому концентровано виражені механістичні уявлення про простір, час і рух, є принцип відносності Галілея (ПВГ), що говорить: закони механіки формулюються однаково у всіх ІСВ, пов'язаних між собою перетвореннями Галілея (див. частина I, гл. 1, §…).Зі сказаного ясно, що зміна уявлень про простір, час і рух у новій фізичній теорії (у даному випадку, у СТВ) тісно зв'язана зі зміною принципу відносності теорії (у даному випадку, ПВГ).
Першою фізичною теорією, що суперечить ПВГ, виявилася електродинаміка Максвела. Дійсно, легко переконатися, що рівняння Максвела (5.1) – (5.4) неінваріантні щодо перетворень Галілея, тобто формулюються неоднаково в різних галілеєвських ІСВ. З іншого боку, у заданій ("нерухомої") ІСВ ці рівняння безумовно справедливі. Таким чином, у наявності протиріччя між електродинамікою і ПВГ.
Для усунення протиріччя, що створилося, можна стати на одну з наступних точок зору (в історії фізики були спроби реалізувати кожну з них):
1) справедливі і закони механіки, і закони електродинаміки; ПВГ же справедливий тільки для механічних явищ: електродинаміка не повинна підкоряться ПВГ у силу специфіки електромагнітного поля. Але якщо послідовно дотримуватися цієї точки зору, то потрібно визнати, що за допомогою електромагнітних явищ можна виділити переважну ІСВ, а це суперечить результатам експериментів з електромагнітними хвилями (наприклад, досвіду Майкельсона – Морлі);
2) ПВГ справедливий (без змін)дляусіх фізичних явищ (у тому числі і для електромагнітних), тобто всі закони фізики повинні бути інваріантні щодо перетворень Галілея; отже рівняння Максвела (які суперечать ПВГ) необхідно модифікувати (змінити). Ясно, що ця точка зору також приходить до протиріччя з експериментом, тому що рівняння Максвела мають надійне експериментальне підтвердження й обґрунтування;
3) закони електродинаміки (5.1) - (5.4) справедливі у всіх ІСВ, тобто електродинаміка (як і інші закони фізики) також задовольняє деякому принципу відносності, однак цим принципом не може бути ПВГ, справедливість якого обмежена тільки рамками класичної механіки. Таким чином, ця точка зору націлює на пошук таких правил перетворення при переході від однієї ІСВ до іншої (відмінних від перетворення Галілея), щоб виконувалися наступні вимоги:
а) рівняння (5.1) - (5.4) були інваріантні щодо цих перетворень;
б) закони класичної механіки не можуть бути інваріантні щодо цих перетворень, тому закони механіки Ньютона необхідно модифікувати (узагальнити) так, що б ці нові закони механіки вже були б інваріантні щодо нових перетворень координат і часу; при цьому нові шукані перетворення від однієї ІСВ до іншої (які ми надалі назвемо перетвореннями Лоренца) і нові закони механіки (які надалі ми будемо називати релятивістською механікою) повинні бути зв'язані з перетворенням Галілея і законами Ньютона за принципом відповідності (див. частина I, Вступ).
Альберт Ейнштейн у своїх дослідженнях став саме на останню (третю з перерахованих) точку зору, що привело його до швидкої й успішної побудови СТВ. Він першим усвідомив значення факту сталості швидкості поширення електромагнітних хвиль (зокрема світла) у вакуумі і фундаментальне значення принципу відносності для фізичної теорії і поклав тому в основу СТВ наступні два фізичних постулати (постулати СТВ):
1) спеціальний принцип відносності Ейнштейна (ПВЕ):
усі закони фізики формулюються однаково у всіх ІСВ, зв'язаних між собою перетвореннями Лоренца (фізичні закони, що задовольняють ПВЕ, називаються релятивістськи інваріантними законами: математичний запис таких законів не залежить від вибору ІСВ);
2) принцип сталості швидкості світла: швидкість світла у вакуумі не залежить від руху джерела світла, однакова у всіх ІСВ і дорівнює електродинамічної постійний с » 2.99792458×108 м/сек.
Зауваження 1. ПВЕ і ПВГ розрізняються в двох важливих пунктах:
