Studying the phenomenon of interference
Оптика
Для студентів інженерно-технічних спеціальностей
денної форми навчання
Методичні вказівки до лабораторних робіт з фізики. Оптика. Для студентів інженерно-технічних спеціальностей денної форми навчання / Укладачі: Лоскутов С.В.., Правда М.І., Лущин С.П., Серпецький Б.О – Запоріжжя: ЗНТУ, 2011 . - 90 с.
У к л а д а ч і: Лоскутов С.В., професор, д-р. фіз-матем. наук.; Правда М.І., канд. фіз.-матем. наук, доцент; Лущин С.П., канд. фіз.-матем. наук, доцент; Серпецький Б.О., канд. фіз.-матем. наук, доцент.
Р е ц е н з е н т и: Курбацький В.П., канд. фіз.-матем. наук, доцент; Сокол Т.О., старший викладач кафедри іноземної мови.
Затверджено на засіданні кафедри фізики ЗНТУ,
протокол № 10 від 04.07.2011 р .
Відповідальний за випуск: Правда М.І. канд. фіз.-матем. наук, доцент.
ЗМІСТ
Вступ . . . . . . . . . .. . . . . ……. . . . . ………………………………….........4
1 Лабораторна робота № 61 Дослідження явища інтерференції світла……………………………………………………………………….......5
2 Лабораторна робота № 62 Дослідження дифракції Фраунгофера на щілині…………………………………………………………………..…10
3 Лабораторна робота № 63 Дифракція на дифракційній решітці ….18
4 Лабораторна робота № 64 Дослідження поляризованого світла…..23
5 Лабораторна робота № 65 Перевірка закону Стефана-Больцмана...29
6 Лабораторна робота № 66 Побудова дисперсійної кривої монохроматора УМ-2……………………………………………………………..34
7 Лабораторна робота № 67 Дослідження спектру атома водню...…38
8 Лабораторна робота № 68. Визначення показника заломлення рідини за допомогою рефрактометра………………………..………...….…….42
9 Laboratory work № 61 Studing the phenomenon of interference……...47
10 Laboratory work № 63 Investigation phenomena of polarization
of light ……………………………………………………………….…..49
11 Laboratory work № 65 Study of energy levels of a hydrogen atom…..53
12 Лабораторна робота № 62.1 дослідження явища інтерференції світла (комп’ютерний вар.)……………..…………………………………...58
13 Laboratory work № 62.1 Study of the phenomenon of light interference (cjmputer var.)……………………………….…………………………....61
14 Лабораторна робота № 64.1 Дослідження дифракції Фраунгофера на дифракційній решітці (комп’ютерний вар.)………………………..63
15 Laboratory work № 64.1 Study of difraction Fraunhofer on difraction grating (computer var.)………………………………………………........66
16 Лабораторна робота № 69 Дисперсія світла (комп’ютерний вар.)..68
17 Laboratory work № 69 Dispersion of light (computer var.)…………..69
18 Лабораторна робота № 70 Фотоефект (комп’ютерний вар.)………70
19 Laboratory work № 70 Photoeffect (computer var.)…………………..72
20 Лабораторна робота № 71 Атомні спектри (комп’ютерний вар.)…74
21 Laboratory work № 71 Atomic spectrum (computer var.)……….……75
22 Газовий лазер ……………………...……………………...………….76
23 Laser………………………………………………………………...…88
ВСТУП
Методичні вказівки містять лабораторні роботи для студентів усіх спеціальностей.
Головна спрямованість методичних вказівок з предмету фізика - дати можливість студентам за допомогою досліду вивчити важливі фізичні явища. Опис лабораторних робіт не претендує на те, щоб створити у студентів повне уявлення про явища, які вивчаються. Таке уявлення може виникнути лише внаслідок опрацювання лекцій та підручників.
Велика увага в методичних вказівках з фізики для студентів технічних спеціальностей приділяється обробленню результатів вимірювань. Для успішного виконання робіт необхідна попередня самостійна підготовка, в першу чергу теоретична.
Кожна лабораторна робота розрахована на дві академічні години занять у лабораторії. Перед заняттям студент повинен підготувати протокол лабораторної роботи, вивчивши відповідний теоретичний матеріал.
Під час заняття студенти проводять необхідні виміри, виконують розрахунки, доводять звіт до висновку. Результати вимірювання обговорюються з викладачем і затверджуються.
Повністю оформлений звіт по лабораторній роботі потрібно подати викладачу до кінця заняття. Він повинен містити: титульний лист, номер лабораторної роботи та її назву, перелік приладів і приладдя, мету роботи, схему установки, розрахункові формули, таблицю результатів вимірів і розрахунки, висновки за результатами роботи. Графіки повинні бути виконані на міліметровому папері.
Якщо студент не встигає захистити лабораторну роботу до кінця заняття, дозволяється оформити звіт (графіки) з використанням комп’ютерних програм (Excel, Origin) до наступного заняття.
Лабораторна робота вважається виконаною після успішно проведеного захисту шляхом співбесіди студента з викладачем (захист звіту + оцінка за теоретичний матеріал).
Захист звіту: мета роботи + експериментальна методика + висновки.
Теоретичний матеріал: знання фізичних явищ, які вивчалися у даній лабораторній роботі (закони, формули).
1 ЛАБОРАТОРНА РОБОТА № 61. ДОСЛІДЖЕННЯ ЯВИЩА ІНТЕРФЕРЕНЦІЇ СВІТЛА
Мета роботи - дослідити явище інтерференції. Визначити довжину хвилі лазерного випромінювання.
Прилади і обладнання: лазер, подвійна щілина, екран, лінійка.
Теоретична частина
Явище інтерференції полягає у перерозподілі світлового потоку у просторі при накладанні когерентних хвиль. Когерентними називаються хвилі, які мають однакову частоту і сталу у часі різницю фаз.
Розглянемо накладання хвиль від двох точкових джерел S 1та S2, які випромінюють монохроматичне світло однакової частоти (рис.2.1).
Зафіксуємо у просторі довільну точку спостереження – т.Р. Для того щоб потрапити у т.Р
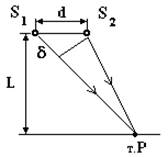
Рисунок 1.1
світло від джерела S 1 проходить шлях l1, а від джерела S2 - шлях l2. Величина:
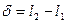 (1.1)
(1.1)
називається різницею ходу променів, а величина
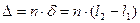 (1.2)
(1.2)
називається оптичною різницею ходу, де n - абсолютний показник заломлення середовища, в якому розповсюджується світло.
Якщо на оптичній різниці ходу Δ вміститься ціла кількість довжин хвиль, тобто якщо буде виконуватись умова
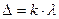 , (1.3)
, (1.3)
де 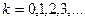 , то в довільну точку спостереження - Р. хвилі від джерел S 1 та S2 прийдуть в одній фазі і при накладанні посилять одна одну, так що в точці Р. виникне максимум інтенсивності світла. Тому умова (1.3) називається умовою інтерференційного максимуму.
, то в довільну точку спостереження - Р. хвилі від джерел S 1 та S2 прийдуть в одній фазі і при накладанні посилять одна одну, так що в точці Р. виникне максимум інтенсивності світла. Тому умова (1.3) називається умовою інтерференційного максимуму.
Якщо на оптичній різниці ходу Δ вміститься напівціла кількість довжин хвиль, тобто якщо буде виконуватись умова
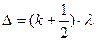 , (1.4)
, (1.4)
де 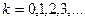 , то в довільну точку спостереження - Р. хвилі від джерел S 1 та S 2 прийдуть у протилежних фазах і при накладанні послаблять одна одну, так що в точці Р. виникне мінімум інтенсивності світла. Тому умова (1.4) називається умовою інтерференційного мінімуму.
, то в довільну точку спостереження - Р. хвилі від джерел S 1 та S 2 прийдуть у протилежних фазах і при накладанні послаблять одна одну, так що в точці Р. виникне мінімум інтенсивності світла. Тому умова (1.4) називається умовою інтерференційного мінімуму.
Експериментальна частина
Для експериментального дослідження явища інтерференції направимо промінь лазера (1) на дві близько розташовані одна від
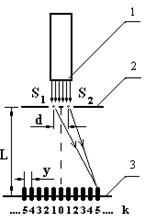
Рисунок 1.2
одної щілини (2) (рис. 1.2) Ширина кожної щілини та відстань між ними дорівнюють приблизно 0,1 мм. Щілини освітлені лазером в такий спосіб являють собою два монохроматичних джерела світла, крім того кожна точка у просторі за щілинами має певне фіксоване значення різниці фаз коливань, що накладаються одне на одне. Тобто ми маємо два когерентних джерела світла. В результаті у просторі за щілинами утворюється сталий перерозподіл інтенсивності світла з максимумами та мінімумами інтенсивності. Якщо за щілинам розмістити екран (3), то на ньому утвориться інтерференційна картина мінімумів та максимумів інтенсивності світла, які чергуються.
З геометрії задачі отримуємо формулу для зв’язку між величинами
 , (1.5)
, (1.5)
де y - відстань між сусідніми максимумами; λ - довжина хвилі; L- відстань між щілинами та екраном; d - відстань між щілинами.
З формули (1.5) для довжини хвилі одержуємо
 . (1.6)
. (1.6)
2.3 Хід роботи
1.Направити промінь лазера на дві щілини та отримати на екрані інтерференційну картину.
2.Виміряти відстань L між щілинами та екраном.
3.Зафіксувати на міліметровому папері інтерференційну картину, яка б складалася щонайменше з трьох груп ярких інтерференційних максимумів (рис. 1.3).
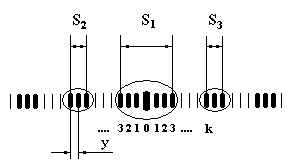
Рисунок 1.3
4.Для розрахунку довжини хвилі за формулою (1.6) необхідно виміряти середню відстань між сусідніми максимумами - 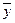 , але ця відстань занадто мала, щоб її можна було виміряти звичайною міліметровою лінійкою. Тому підрахуємо кількість ярких максимумів в центральній групі максимумів. Нехай ця кількість дорівнює
, але ця відстань занадто мала, щоб її можна було виміряти звичайною міліметровою лінійкою. Тому підрахуємо кількість ярких максимумів в центральній групі максимумів. Нехай ця кількість дорівнює 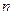 , а проміжків між ними (а це саме і є відстань y) буде
, а проміжків між ними (а це саме і є відстань y) буде 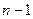 . Виміряємо відстань S 1, між крайніми максимумами в цій групі. Аналогічно виміряємо відстані S2 , S 3, так як показано на рис. 1.3 і обчислимо відповідно три значення
. Виміряємо відстань S 1, між крайніми максимумами в цій групі. Аналогічно виміряємо відстані S2 , S 3, так як показано на рис. 1.3 і обчислимо відповідно три значення 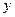 за формулами:
за формулами:
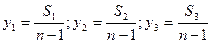 . (1.7)
. (1.7)
Результати вимірювань занесемо в таблицю 1.1.
Таблиця 1.1 
| № | Si , мм | yi , мм | 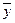 , мм , мм | L , мм | d , мм | λ , мм |
| 0,22 | ||||||
5. За формулою (1.6), користуючись середнім значенням 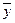 , розрахувати довжину хвилі лазерного випромінювання в міліметрах, одержаний результат перевести в метри і остаточно в нанометри. Експериментальне значення λ порівняти з табличним.
, розрахувати довжину хвилі лазерного випромінювання в міліметрах, одержаний результат перевести в метри і остаточно в нанометри. Експериментальне значення λ порівняти з табличним.
6. Похибки вимірювань обчислити за формулами (1.8) – (1.12).
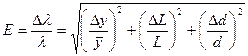 ; (1.8)
; (1.8)
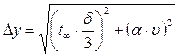 ,де
,де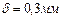 ,
, 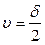 ;(1.9)
;(1.9)
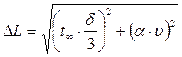 , де
, де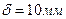 ,
, 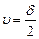 ; (1.10)
; (1.10)
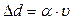 ,де
,де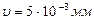 ;(1.11)
;(1.11)
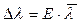 . (1.12)
. (1.12)
6. Остаточний результат вимірів довжини хвилі λ представити у вигляді
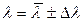 . (1.13)
. (1.13)
Порівняти одержаний результат з табличним значенням:
λ табл. = 630 нм
Контрольні запитання
1.В чому полягає явище інтерференції світла?
2.Які джерела хвиль називають когерентними?
3.Що таке оптична різниця ходу?
4.Якими формулами визначаються умови інтерференційного максимуму та мінімуму?
Література
1.Ландcберг Г. С. Оптика. – М.: Наука, 1976.- с. 62 – 94.
2.Сивухин Д. В. Общий курс физики. – т. 4. – М.: Наука, 1980.- с 188- - 256.
3.Савельев И. В. Курс общей физики.– т. 2. – М.: Наука, 1982.- с. 347 – 374.
2 ЛАБОРАТОРНА РОБОТА № 62. ДОСЛІДЖЕННЯ ДИФРАКЦІЇ ФРАУНГОФЕРА НА Щ1ЛИНІ
Мета роботи -дослідити явище дифракції на одній щілині.
Прилади і обладнання: лазер, щілина, екран, лінійка.
Теоретична частина
В початковому вузькому сенсі дифракція це є огинання хвилями перешкод, у сучасному, більш широкому – будь-яке відхилення від законів геометричної оптики при розповсюдженні хвиль. Дифракцією називають сукупність явищ при розповсюдженні світла в середовищі з різкими неоднорідностями, такими як маленький круглий отвір, вузька щілина, дифракційна решітка тощо. В звичайних умовах дифракцію світла спостерігають у вигляді нерізкої розмитої границі тіні освітленого предмета.
Між явищами інтерференції та дифракції немає принципової фізичної різниці. Обидва ці явища полягають у перерозподілі світлового потоку при суперпозиції (накладанні) когерентних хвиль. Але при суперпозиції хвиль від точкових джерел говорять про інтерференцію, а при суперпозиції хвиль від джерел, які мають певні кінцеві розміри говорять про дифракцію.
Явища дифракції зазвичай класифікують в залежності від відстаней між джерелом i точкою спостереження (екраном) та перешкодою, що розташована на шляху світла. Якщо ці відстані великі (нескінченно великі) то говорять про дифракцію в паралельних променях – дифракцію Фраунгофера. У протилежному випадку говорять про дифракцію в непаралельних променях – дифракцію Френеля.
Простим для розрахунку та практично важливим випадком дифракції є дифракція на довгій прямокутній щілині. Світлове поле за щілиною знайдеться за принципом Гюйгенса-Френеля, який полягає в наступному: кожна точка хвильового фронту є джерелом вторинних хвиль, притому інтенсивність світла у довільній точці простору можна розглядати як результат інтерференції вторинних хвиль, які випромінюються нескінченно малими ділянками хвильової поверхні.
При застосуванні принципу Гюйгенса-Френеля на випадок щілини, будемо розглядати інтенсивність світла у довільній точці спостереження як результат інтерференції когерентних вторинних хвиль, що випромінюються різними ділянками хвильового фронту на щілині.
Нехай на щілину шириною 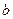 нормально падає плоска монохроматична хвиля довжиною
нормально падає плоска монохроматична хвиля довжиною  . Розглянемо інтерференційну картину на екрані, який розташований на відстані L >> b від щілини – ця умова є умовою дифракції Фраунгофера (рис.2.1).
. Розглянемо інтерференційну картину на екрані, який розташований на відстані L >> b від щілини – ця умова є умовою дифракції Фраунгофера (рис.2.1).
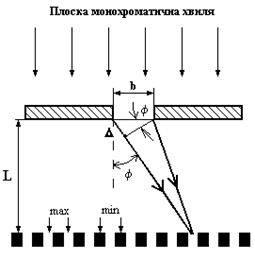
Рисунок 2.1
Інтерференційна картина буде являти собою чергування на екрані світлих (max), та темних (min) смуг. Умова дифракційного мінімуму в цьому випадку має вигляд
 , (2.1)
, (2.1)
де  - кут дифракції;
- кут дифракції; 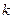 - порядок дифракційного мінімуму;
- порядок дифракційного мінімуму; 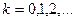
А умова дифракційного максимуму виглядає
 , (2.2)
, (2.2)
де 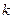 - порядок дифракційного максимуму;
- порядок дифракційного максимуму; 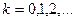
Умова (2.1) означає: різниця ходу 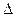 між хвилями, що випромінюються крайніми точками щілини, повинна містити ціле число хвиль
між хвилями, що випромінюються крайніми точками щілини, повинна містити ціле число хвиль
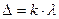 , (2.3)
, (2.3)
В той же час з геометрі задачі маємо:
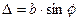 . (2.4)
. (2.4)
Одержаний результат легко пояснити без будь-яких розрахунків. Припустимо, з початку, що  і формула (2.1) приймає вигляд
і формула (2.1) приймає вигляд
 . (2.5)
. (2.5)
Розділимо щілину на дві рівні частини. Тоді хвилі від цих частин щілини прийдуть в певну точку спостереження, для якої виконується умова 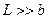 , в протилежних фазах i погасять одна одну при інтерференції – утвориться min інтенсивності 1-го порядку. Якщо ж виконується умова (2.1), то щілину треба розділити на 2k ділянок однакової ширини. Хвилі від ділянок з непарними номерами прийдуть в певну точку спостереження в фазах, протилежних фазам хвиль, що прийшли від частин з парними номерами.
, в протилежних фазах i погасять одна одну при інтерференції – утвориться min інтенсивності 1-го порядку. Якщо ж виконується умова (2.1), то щілину треба розділити на 2k ділянок однакової ширини. Хвилі від ділянок з непарними номерами прийдуть в певну точку спостереження в фазах, протилежних фазам хвиль, що прийшли від частин з парними номерами.
Експериментальна частина
Схему лабораторної установки, яка складається з лазера (1), щілини (2) та екрану (3) представлено на рис. 2.2.
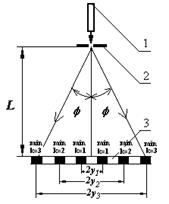
Рисунок 2.2
Завдання 1. Визначити ширину щілини по відомій довжині хвилі  .
.
Порядок виконання:
1.Направити промінь лазера (1) на щілину (2) та отримаємо на екрані (3) інтерференційну картину мінімумів та максимумів інтенсивності світла, що чергуються (рис.3.2).
2. Виміряти відстань від щілини до екрану  .
.
3. Зафіксувати на міліметровому папері інтерференційну картину, яка повинна містити не менше трьох мінімумів та максимумів інтенсивності світла в обидві сторони від центрального – нульового максимуму (рис.2.2). Виміряємо відстані між двома мінімумами 1-го порядку - 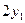 , 2-го порядку -
, 2-го порядку - 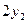 , та 3-го порядку -
, та 3-го порядку -  . Величини
. Величини 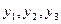 занесемо в таблицю 3.1.
занесемо в таблицю 3.1.
Таблиця 2.1
| k | y , мм | b , мм | L , мм | λ ,мм | 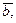 мм мм |
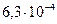 | |||||
4. Враховуючи, що при малих кутах  , формула (2.1) може бути записана у вигляді
, формула (2.1) може бути записана у вигляді
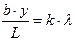 , (2.6)
, (2.6)
звідки для ширини щілини одержуємо
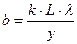 . (2.7)
. (2.7)
4.За формулою (2.7) для 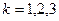 розрахувати три значення
розрахувати три значення 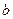 та знайти середнє значення ширини щілини
та знайти середнє значення ширини щілини 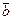 .
.
5.Розрахувати відносну похибку вимірювань Е за формулою
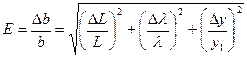 . (2.8)
. (2.8)
Абсолютні похибки величин 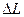 ,
, 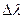 ,
, 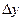 визначити за формулами
визначити за формулами
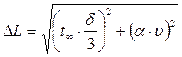 , де
, де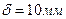 ,
, 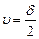 ; (2.9)
; (2.9)  ,де
,де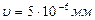 ;(2.10)
;(2.10)
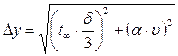 ,де
,де 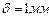 ,
, 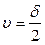 . (2.11)
. (2.11)
7. Оцінити абсолютну похибку вимірювань довжини хвилі Dl за формулою
 , (2.12)
, (2.12)
8.Остаточний результат вимірів довжини хвилі  представити у вигляді
представити у вигляді
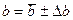 .(2.13)
.(2.13)
Завдання 2. Дослідити залежність інтерференційної картини при дифракції на щілині від її ширини. Перевірити умову інтерференційного максимуму при дифракції на щілині.
Порядок виконання:
1.Направити промінь лазера (1) на щілину (2), ширину якої можна регулювати за допомогою мікрометричного гвинта, та отримаємо на екрані (3) інтерференційну картину мінімумів та максимумів інтенсивності світла, що чергуються (рис.2.2).
2. Дослідити спочатку якісно залежність інтерференційної картини від ширини щілини.Із зменшенням ширини щілини відстань кожного мінімуму від центра картини зростає, центральна світла смуга розширюється і захоплює все більшу частину екрана, а освітленість прямує стати рівномірною по всьому екрану. І навпаки, при збільшенні ширини щілини положення перших мінімумів присувається все ближче до центру картини, а центральні максимуми стають все більш чіткими.
3. Виміряти відстань L від щілини до екрана.
4. Встановити за допомогою мікрометричного гвинта ширину щілини b = 0. Обертаючи мікрометричний гвинт, збільшувати щілину i слідкувати за змінами дифракційної картини на екрані. Намалювати на міліметровому папері дифракційну картину при п’яти значеннях b в діапазоні b = 0,05… 0,25 мм з кроком 0,05 мм (рис.2. 3).

Рисунок 2.3
3. Виміряти відстані між мінімумами 1 – 3 порядків: 2y1, 2y2, 2y3 (рис.2.3).. Величини y1, y2, y3 занести в таблицю 3.2.
Таблиця 2.2
| № | b, мм | Експеримент | Теорія | L, мм | ||||
| y, мм | y, мм | |||||||
| k = 1 | k = 2 | k = 3 | k = 1 | k = 2 | k = 3 | |||
5. Приймаючи до уваги, що у формулі (2.1) при малих кутах  , для величини
, для величини 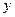 одержуємо:
одержуємо:

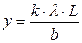 . (2.14)
. (2.14)
Використовуючи формулу (214), розрахувати теоретичні значення величин у1, y2, y3 в залежності від b. Прийняти, що довжина хвилі випромінювання лазера дорівнює 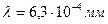 .
.
Данні занести в таблицю 2.2.
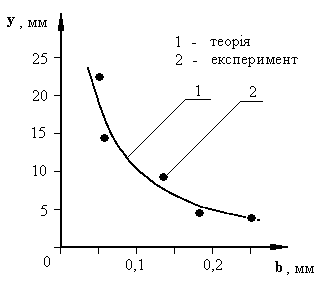
Рисунок 2.4
4. Побудувати три графіка залежностей 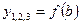 для максимумів перших трьох порядків при k = 1,2,3 (рис. 2.4). У висновку відобразити результати експериментальної перевірки умови дифракційного мiнiмуму - формули (2.1).
для максимумів перших трьох порядків при k = 1,2,3 (рис. 2.4). У висновку відобразити результати експериментальної перевірки умови дифракційного мiнiмуму - формули (2.1).
Контрольні запитання
1.Яке явище називається дифракцією світла?
2.Що таке різниця ходу світових хвиль?
3.Написати умови виникнення дифракційного мінімуму та максимуму інтенсивності.
4.Як формулюється принцип Гюйгенса-Френеля?
Література
1. Ландcберг Г. С. Оптика. – М.: Наука, 1976.- с.150 – 219.
2. Сивухин Д. В. Общий курс физики. – т. 4. – М.: Наука, 1980.- 262 – 298.
3. Савельев И. В. Курс общей физики.– т. 2. – М.: Наука, 1982.- 381 – 400.
3 ЛАБОРАТОРНА РОБОТА № 63. ДИФРАКЦІЯ НА ДИФРАКЦІЙНІЙ РЕШІТЦІ
Мета роботи: 1. Перевірити умову дифракційного максимуму при дифракції на дифракційній решітці.
2. Визначити довжину хвилі лазерного випромінювання.
Прилади та обладнання: дифракційна решітка, лазер, екран, лінійка.
Теоретична частина
У вузькому розумінні під дифракцією розуміють огинання світловими хвилями перешкод. Дифракцією (від лат. difractus – розламаний, заломлений) називають сукупність явищ при розповсюдженні світла в середовищі з різкими неоднорідностями. Важливою для практичного застосування є дифракція на дифракційній решітці – оптичному приладі, який являє собою періодичну структуру, яка складається з великої кількості регулярно розташованих елементів, наприклад паралельних штрихів, які знаходяться на однаковій відстані один від одного. Дифракційні решітки, що застосовуються для роботи в різних областях спектру, відрізняються розмірами, формою, матеріалом поверхні, профілем штрихів та їх частотою (від 6000 штрих / мм для рентгенівських променів до 0,25 штрих / мм для інфрачервоного діапазону). Головна властивість дифракційної решітки – її здатність розкладувати складне світло по довжинам хвиль, тому дифракційна решітка застосовуються у якості диспергуючого елемента в спектральних приладах. На дифракційній решітці здійснюється багатопроменева інтерференція когерентних пучків дифрагованого світла, які випромінюються щілинами решітки при її освітленні. Нехай на дифракційну решітку нормально до її поверхні падає плоска монохроматична хвиля. Різниця ходу між вторинними хвилями, що випромінюються сусідніми щілинами решітки буде дорівнювати 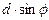 , а різниця фаз становить
, а різниця фаз становить
 , (3.1)
, (3.1)
де k – хвильове число, d – період дифракційної решітки (сума довжин прозорого та непрозорого проміжків), а j - кут дифракції.
У випадку, коли 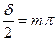 , з формули (3.1) одержуємо:
, з формули (3.1) одержуємо:
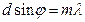 , (3.2)
, (3.2)
де m = 0, 1, 2, …
В напрямках, що визначаються формулою (3.2), утворюються максимуми інтенсивності, які в N2 разів перевершують інтенсивності хвилі від однієї щілини в тому самому напрямку. Ці максимуми називаються головними максимумами. Ціле число m називається порядком головного максимуму, або порядком спектру. Знаючи положення головних максимумів, можна розрахувати довжину хвилі l за формулою (3.2).
3.2 Хід роботи
Схема лабораторної установки представлена на рис.3.1 Промінь лазера 1 освітлює щілини дифракційної решітки 2 так, що у просторі за решіткою утворюються мінімуми та максимуми інтенсивності, спостерігати які можна на екрані 3.
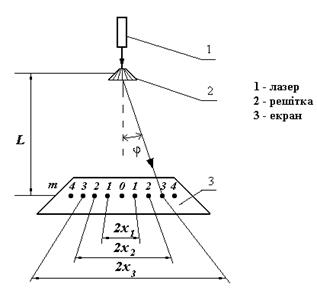
Рисунок 3. 1
1.Виміряти відстань від дифракційної решітки до екрану L.
2. Зафіксувати в зошиті положення максимумів 1-го, 2-го, …,5-го порядків. Виміряти відстань між максимумами 1-го, 2-го, …,5-го порядків 2 x 1 , 2 x2 ,…, 2 x5 . Якщо кут φ малий, то буде виконуватись умова
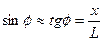 . (3.3)
. (3.3)
При цьому формула (3.2) може бути записана у вигляді
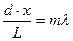 . (3.4)
. (3.4)
3.Позначимо через 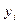 величину
величину

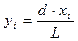 , (3.5)
, (3.5)
тобто
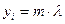 . (3.6)
. (3.6)
4. За формулою (3.6) розрахувати 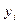 . Дані занести в таблицю 3.1.
. Дані занести в таблицю 3.1.
5. Експериментальні результати представити в графічному вигляді 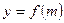 . Згідно формули (3.6) цей графік повинен бути лінійним. Через експериментальні точки провести найкращу пряму, яка б проходила через максимальну густину точок. По графіку визначити середнє значення довжини хвилі лазерного випромінювання
. Згідно формули (3.6) цей графік повинен бути лінійним. Через експериментальні точки провести найкращу пряму, яка б проходила через максимальну густину точок. По графіку визначити середнє значення довжини хвилі лазерного випромінювання 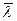 як
як 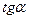 (рис. 3.2) за формулою:
(рис. 3.2) за формулою:
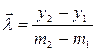 , (3.7)
, (3.7)
де (m1, y1) та (m2, y2) дві довільні точки на графіку, але не експериментальні дані з таблиці 3.1.
6. Зробити висновок щодо справедливості умови дифракційного максимуму при дифракції на решітці - формули (3.2): якщо графік лінійний, то формула (3.2) справедлива.
Таблиця 3.1
| m | x i , мм | yi, мм | d, мм | L, мм | 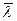 , нм , нм |
| 0.032 | |||||

Рисунок 3. 2
4. Розрахувати відносну похибку вимірювань Е за формулою
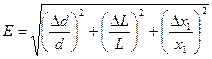 .
.  (3.8)
(3.8)
Абсолютні похибки величин 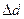 ,
, 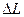 ,
, 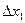 визначити за формулами:
визначити за формулами:
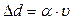 ,де
,де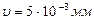 ;(3.9)
;(3.9)
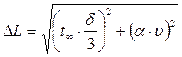 , де
, де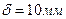 ,
, 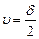 ; (3.10)
; (3.10)
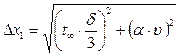 , де
, де 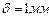 ,
, 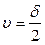 . (3.11)
. (3.11)
8. Оцінити абсолютну похибку вимірювань довжини хвилі Dl за формулою
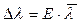 , (3.12)
, (3.12)
9.Остаточний результат вимірів довжини хвилі  представити у вигляді:
представити у вигляді:
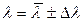 . (3.13)
. (3.13)
Порівняти одержаний результат з табличним значення 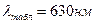 .
.
Контрольні запитання
1.Яке явище називається дифракцією світла?
2.Що таке дифракційна решітка, для чого вона призначена?
3.Чому дифракційна решітка розкладує світло в спектр?
4.Різниця ходу та різниця фаз при дифракції на дифракційній решітці.
5.Написати умови виникнення дифракційного максимуму інтенсивності при дифракції на дифракційній решітці.
Література
1. Ландcберг Г. С. Оптика. – М.: Наука, 1976.- с. 198 – 204.
2. Сивухин Д. В. Общий курс физики. – т. 4. – М.: Наука, 1980.- с. 302 – 312.
3. Савельев И. В. Курс общей физики.– т. 2. – М.: Наука, 1982.- с. 407 – 415.
4. Физический энциклопедический словарь.- М.: СЭ, 1999.- с. 169.
4 ЛАБОРАТОРНА РОБОТА № 64. ДОСЛІДЖЕННЯ ПОЛЯРИЗОВАНОГО СВ1ТЛА
Мета роботи - Ознайомитись з явищем поляризації. Перевірити закон Малюса.
Прилади і обладнання: лазер, поляроїд-аналізатор, фотодіод, міліамперметр.
Теоретична частина
Світло являє собою електромагнітну хвилю, в якій у взаємно перпендикулярних площинах відбуваються коливання векторів напруженості електричного 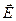 та магнітного
та магнітного 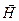 полів. Вектор швидкості хвилі
полів. Вектор швидкості хвилі 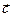 перпендикулярний обом цим векторам, так що вектори
перпендикулярний обом цим векторам, так що вектори 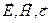 складають правобічну трійку векторів. Тобто розповсюдження електромагнітної хвилі відбувається у напрямку, який перпендикулярний площинам в яких відбуваються коливання напруженості електричного та магнітного полів. Це означає, що електромагнітна хвиля поперечна (рис.4.1).
складають правобічну трійку векторів. Тобто розповсюдження електромагнітної хвилі відбувається у напрямку, який перпендикулярний площинам в яких відбуваються коливання напруженості електричного та магнітного полів. Це означає, що електромагнітна хвиля поперечна (рис.4.1).
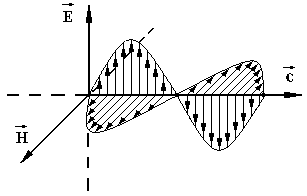
Рисунок 4.1
Перехрестя векторів 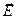 та
та 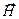 може бути зорієнтоване у просторі як завгодно відносно напрямку розповсюдження променя – вектора
може бути зорієнтоване у просторі як завгодно відносно напрямку розповсюдження променя – вектора 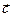 . В природному світлі ця орієнтація змінюється хаотично (осьова симетрія). Площина в якій водночас знаходяться вектори
. В природному світлі ця орієнтація змінюється хаотично (осьова симетрія). Площина в якій водночас знаходяться вектори 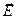 та
та 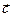 називається площиною коливань, або площиною поляризації. У площині поляризації відбуваються коливання вектора
називається площиною коливань, або площиною поляризації. У площині поляризації відбуваються коливання вектора 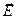 і у природному світлі ці коливання відбуваються рівно ймовірно по всіх напрямках (рис.4.2а).
і у природному світлі ці коливання відбуваються рівно ймовірно по всіх напрямках (рис.4.2а).
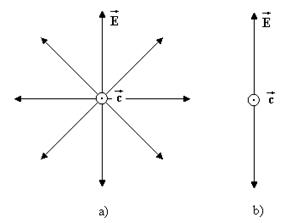
Рисунок 4.2
Світло, в якому площина коливань не змінюється хаотично, а має певну орієнтацію у просторі (рис.4.2b), називається поляризованим. Таке світло можна одержати, якщо природне світло пропустити через деякі природі кристали, які поглинають світлові промені у котрих електричний вектор перпендикулярний до їх оптичної осі. Промені ж, у яких електричний вектор паралельний до оптичної осі кристала, проходять через нього практично без поглинання. Таку ж саму властивість мають штучно виготовлені поляроїди. Тобто після проходження через поляроїд природне світло (рис.4.2а) перетворюється на поляризоване (рис.4.2b). Поляроїд, який використовується для одержання поляризованого світла називається поляризатор, а поляроїд, який використовується для дослідження поляризованого світла називається аналізатор.
Поставимо на шляху природного світла два поляроїди – 1 і 2 (рис.4.3а). Після проходження через поляроїд 1 природне світло 3 перетворюється на поляризоване 4. Позначимо через 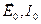 електричний вектор та інтенсивність світлової хвилі, що після проходження через поляризатор 1 падає на аналізатор 2; а через
електричний вектор та інтенсивність світлової хвилі, що після проходження через поляризатор 1 падає на аналізатор 2; а через 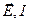 - електричний вектор та інтенсивність світлової хвилі, яка пройшла через два поляроїда.
- електричний вектор та інтенсивність світлової хвилі, яка пройшла через два поляроїда.

Рисунок 4.3
2. Коливання вектора 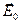 відбуваються у оптичній площині поляризатора, а коливання вектора
відбуваються у оптичній площині поляризатора, а коливання вектора 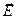 - у оптичній площині аналізатора, тому, як видно з рис.4.3b між величинами
- у оптичній площині аналізатора, тому, як видно з рис.4.3b між величинами 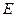 та
та 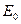 повинно існувати співвідношення:
повинно існувати співвідношення:
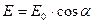 , (4.1)
, (4.1)
де 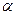 - це кут між площиною поляризації падаючого світла та оптичною площиною аналізатора. Оскільки інтенсивність
- це кут між площиною поляризації падаючого світла та оптичною площиною аналізатора. Оскільки інтенсивність 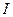 пропорційна квадрату амплітуди
пропорційна квадрату амплітуди 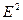 , то для інтенсивності світла
, то для інтенсивності світла 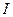 одержуємо:
одержуємо:
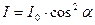 . (4.2)
. (4.2)
Співвідношення (4.2) називається законом Малюса.
Експериментальна частина
Для експериментальної перевірки закону Малюса використовується пристрій, схему якого зображено на рис. 4.4. Промінь від лазера 1 відбивається від дзеркала 2 , проходить через поляроїд 3, і потрапляє на фотодіод 4, який генерує фотострум 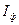 , що фіксується міліамперметром 5.
, що фіксується міліамперметром 5.
Світло більшої інтенсивності призводить до генерації більшого фотоструму. Дослід показує, що фотострум 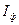 лінійно залежить від інтенсивності світла
лінійно залежить від інтенсивності світла 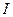 , що потрапляє на фотодіод. Позначимо через
, що потрапляє на фотодіод. Позначимо через 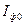 максимальне значення фотоструму. Тоді будуть виконуватись співвідношення:
максимальне значення фотоструму. Тоді будуть виконуватись співвідношення:
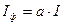 та
та 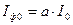 , (4.3)
, (4.3)
де а – певний коефіцієнт пропорційності між інтенсивністю світла та фотострумом. З рівнянь (4.3) одержуємо:
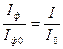 . (4.4)
. (4.4)
З іншого боку відношення 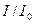 згідно закону Малюса дорівнює
згідно закону Малюса дорівнює 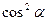 .
.
4.3 Хід роботи
1. Направимо промінь від лазера 1 за допомогою дзеркала 2 через поляроїд 3 на фотодіод 4. При цьому міліамперметр 5 покаже певний
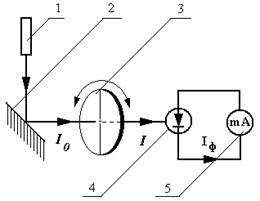
Рисунок 4.4
струм, сила якого залежатиме від інтенсивності світлового потоку.
2.Будемо повільно обертати поляроїд 3 навколо власної осі у якийсь один бік з метою встановити на міліамперметрі 5 максимальне значення струму. Коли фотострум досягне максимального значення 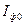 , це означатиме, що площина поляризації лазерного променя співпала з власною оптичною площиною поляроїда; при цьому у формулі (4.2) кут
, це означатиме, що площина поляризації лазерного променя співпала з власною оптичною площиною поляроїда; при цьому у формулі (4.2) кут  .
.
3.Повільно обертаючи поляроїд у якийсь один бік, будемо фіксувати значення фотоструму 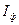 через кожні
через кожні 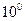 в інтервалі
в інтервалі 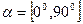 . Данні занесемо в таблицю.
. Данні занесемо в таблицю.
4. Тепер встановимо на міліамперметрі мінімальне значення струму. Це означатиме, що кут 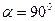 . Пройдемо той самий інтервал
. Пройдемо той самий інтервал 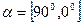 у зворотному напрямку, фіксуючи значення фотоструму
у зворотному напрямку, фіксуючи значення фотоструму 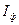 через кожні
через кожні 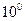 . Знайдемо середнє значення фотоструму
. Знайдемо середнє значення фотоструму  для кожного кута.
для кожного кута.
5.Розрахуємо відношення 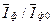 , де
, де  - максимальне значення фотоструму при
- максимальне значення фотоструму при 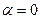 . Данні занесемо в таблицю.
. Данні занесемо в таблицю.
6. Побудуємо графік залежності величини 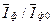 від
від 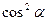 (рис.4.5). Лінійний характер графіку підтверджуватиме справедливість закону Малюса.
(рис.4.5). Лінійний характер графіку підтверджуватиме справедливість закону Малюса.
Таблиця 4.1
| α | cos α | cos2 α | I ф, мА |  | 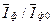 | |
| 0,98 | 0,97 | |||||
| 0,94 | 0,88 | |||||
| 0,87 | 0,75 | |||||
| 0,76 | 0,59 | |||||
| 0,64 | 0,41 | |||||
| 0,50 | 0,25 | |||||
| 0,34 | 0,12 | |||||
| 0,17 | 0,03 | |||||
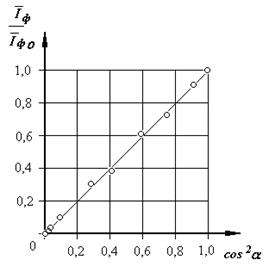
Рисунок 4.5
7.Зробити висновки щодо справедливості закону Малюса.
Контрольні запитання
1. Що таке світло з сучасної наукової точки зору?
2.Як в електромагнітній хвилі орієнтовані один відносно одного вектори 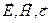 ?
?
3. Що таке площина поляризації?
4.Чим поляризоване світло відрізняється від природного?
5.В чому полягає закон Малюса?.
Література
1. Ландcберг Г. С. Оптика. – М.: Наука, 1976.- с.370 – 379.
2. Сивухин Д. В. Общий курс физики. – т. 4. – М.: Наука, 1980.- с. 397 – 400.
3. Савельев И. В. Курс общей физики.– т. 2. – М.: Наука, 1982.- с. 428 – 432.
5 ЛАБОРАТОРНА РОБОТА № 65. ПЕРЕВІРКА ЗАКОНУ СТЕФАНА-БОЛЬЦМАНА
Мета роботи -Перевірити закон Стефана-Больцмана.
Прилади і обладнання: джерело струму, лампа розжарювання, термостовпчик, міліамперметр.
Теоретична частина
Випромінювання світла відбувається в результаті переходів атомів і молекул із станів з більшою енергією в стани з меншою енергією. Теплове випромінювання відрізняється від інших видів випромінювання (люмінесценції) способом переходу систем, що випромінюють, у збуджені стани. При тепловому випромінюванні такий перехід відбувається за рахунок теплового руху атомів та молекул. Інтенсивність теплового випромінювання характеризується енергетичною світимістю 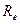 , яка визначається як кількість променевої енергії, що випромінюється одиницею поверхні тіла за одиницю часу, тобто
, яка визначається як кількість променевої енергії, що випромінюється одиницею поверхні тіла за одиницю часу, тобто
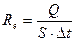 , (5.1)
, (5.1)
де Q – енергія, що випромінюється тілом з площі S за час Dt.
Теплове випромінювання складається з хвиль різної довжини λ. Доля енергетичної світимості, яка припадає на елементарний інтервал dλ має вигляд
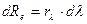 , (5.2)
, (5.2)
тому енергетична світимість може бути представлена у вигляді:
 , (5.3)
, (5.3)
де rλ – емісійна здатність тіла, або густина енергетичної світимості, яка
визначається як:
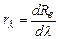 . (5.4)
. (5.4)
Нехай на елементарну площину dS в діапазоні хвиль dλ падає потік променевої енергії dФλ. Частина цього потоку dФ′λ поглинається тілом. Тоді величина:
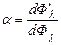 (5.5)
(5.5)
називається поглинальною здатністю тіла.
Тіло, що поглинає випромінювання будь-якої довжини хвилі називається абсолютно чорним. Для абсолютно чорного тіла α = 1 для всіх довжин хвиль. Якщо для деякого тіла α < 1 і для всіх довжин хвиль λ стале, то таке тіло називається сірим.
Згідно з законом Стефана-Больцмана енергетична світимість абсолютно чорного тіла

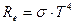 , (5.6)
, (5.6)
а для сірого тіла
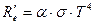 , (5.7)
, (5.7)
де Т – абсолютна температура, а σ – стала Стефана-Больцмана, яка дорівнює: σ » 5,67×10– 8 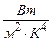 , а величина α < 1, має назву коефіцієнта чорноти.
, а величина α < 1, має назву коефіцієнта чорноти.
Експериментальна частина
Схема лабораторної установки представлена на рис. 1. Джерело струму 1 живить лампу розжарювання 4. Струм та напруга на лампі
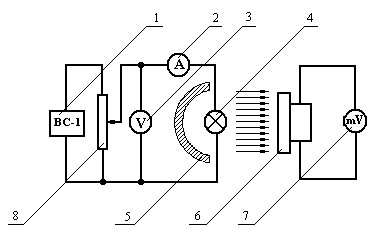
Рисунок 5.1
фіксуються відповідно амперметром 2 та вольтметром 3, що розташовані на джерелі струму 1. Світло від лампи розжарювання відбивається від екрану 5 і потрапляє на термостовпчик 6, що генерує напругу, яка вимірюється міліамперметром 7.
5.3 Хід роботи
1. Перед тим як увімкнути джерело струму в мережу впевнимось, що потенціометр 8 джерела знаходиться у крайньому лівому положенні, при якому струм та напруга на лампі розжарювання дорівнюють нулю. Увімкнемо джерело струму в мережу і повільно обертаючи потенціометр джерела по годинній стрільці, встановимо максимальне значення струму через лампу 5А (не більше!).
2. Зачекаємо приблизно 1 хвилину поки в системі не встановиться стан рівноваги і мілівольтметр 7 покаже певне стале значення напруги, що генерується термостовпчиком 6.
3. Результати вимірів струму та напруги на лампі, а також напругу на термостовпчику занести в таблицю. Поступово зменшуючи струм через лампу, повторити виміри при значеннях сили струму в інтервалі від 5 до 1 амперу з кроком в 0,5 ампера. Після встановлення кожного нового значення струму напругу на термостовпчику - 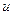 записувати не раніше ніж через 1 хвилину для того, щоб система була в змозі прийти в стан рівноваги. Данні вимірювань занести в таблицю 5.1.
записувати не раніше ніж через 1 хвилину для того, щоб система була в змозі прийти в стан рівноваги. Данні вимірювань занести в таблицю 5.1.
Таблиця 5.1
| № | I ,A | U, B | R , Ом | t , 0 C | T ,K | u, мВ | ln T | ln u |
| 4,5 | ||||||||
| 3,5 | ||||||||
| 2,5 | ||||||||
| 1,5 | ||||||||
4. Для кожної пари значень сили струму 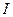 та напруги
та напруги 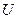 визначити по закону Ома опір нитки накалу лампи розжарювання
визначити по закону Ома опір нитки накалу лампи розжарювання 
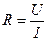 . (5.8)
. (5.8)
Данні занести в таблицю 5.1.
5. Опір лампи розжарювання пов'язаний з температурою її нитки формулою:
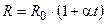 , (5.8)
, (5.8)
де 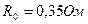 - опір при
- опір при 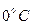 ;
; 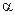 - температурний коефіцієнт опору, який дорівнює:
- температурний коефіцієнт опору, який дорівнює:  ;
; 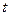 - температура по шкалі Цельсія.
- температура по шкалі Цельсія.
З формули (5.8) знаходимо температуру нитки лампи в градусах Цельсія
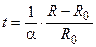 (5.9)
(5.9)
і абсолютну температуру за формулою
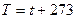 (5.10).
(5.10).
6. Напруга, що виникає в термостовпчику практично лінійно залежить від енергетичної світимості нитки, тобто можна вважати, що
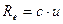 , (5.11)
, (5.11)
де 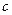 - певна стала величина. З іншого боку згідно закону Стефана-Больцмана енергетична світимість пропорційна четвертому ступеню температури. Для перевірки цього факту, користуючись формулами (5.6) та (5.11) для енергетичної світимості запишемо:
- певна стала величина. З іншого боку згідно закону Стефана-Больцмана енергетична світимість пропорційна четвертому ступеню температури. Для перевірки цього факту, користуючись формулами (5.6) та (5.11) для енергетичної світимості запишемо:
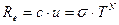 . (5.12)
. (5.12)
Після логарифмування формули (12) одержуємо:
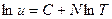 , (5.13)
, (5.13)
де 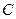 - певна стала величина.
- певна стала величина.
Візьмемо логарифми від напруги 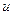 , та температури
, та температури 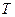 . Данні занесемо в таблицю.
. Данні занесемо в таблицю.
7. Побудуємо графік залежності  від
від 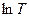 (рис.5.2).
(рис.5.2).
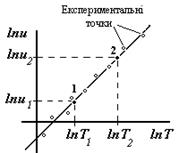
Рисунок 5.2
8. Користуючись побудованим графіком, визначимо показник 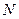 . Для чого виберемо на графіку (але не з таблиці!)дві будь-які довільні точки і розрахуємо
. Для чого виберемо на графіку (але не з таблиці!)дві будь-які довільні точки і розрахуємо 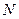 за формулою:
за формулою:
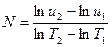 . (5.14)
. (5.14)
Порівняймо одержане значення 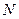 з показником ступеня в законі Стефана-Больцмана.
з показником ступеня в законі Стефана-Больцмана.
Контрольні запитання
1. Яке випромінювання називається тепловим?
2. Що таке енергетична світимість?
3. Що таке густина енергетичної світимості?
4. Як пов’язані між собою енергетична світимість і густина енергетичної світимості?
5. Яке тіло називається абсолютно чорним?
6. В чому полягає закон Стефана-Больцмана?
Література
1. Ландcберг Г. С. Оптика. – М.: Наука, 1976.- с. 682 – 698.
2. Сивухин Д. В. Общий курс физики. – т. 4. – М.: Наука, 1980.- с. 685 – 687.
3. Савельев И. В. Курс общей физики.– т. 3. – М.: Наука, 1982.- с. 16 – 18.
6 ЛАБОРАТОРНА РОБОТА № 66. ПОБУДОВА ДИСПЕРСІЙНОЇ КРИВОЇ МОНОХРОМАТОРА УМ-2
Мета роботи - Побудувати дисперсійну криву монохроматора УМ-2 по відомим довжинам хвиль лінійчатого спектра ртуті.
Прилади і обладнання: Монохроматор УМ-2, ртутна лампа, джерело живлення ЕПС-2.
Теоретична частина
Фізичний зміст абсолютного показника заломлення 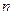 полягає в тому, що він показує, в скільки разів швидкість розповсюдження світла в вакуумі більше швидкості розповсюдження світла у даному середовищі
полягає в тому, що він показує, в скільки разів швидкість розповсюдження світла в вакуумі більше швидкості розповсюдження світла у даному середовищі
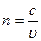 , (6.1)
, (6.1)
де 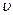 - швидкість розповсюдження світла в даному середовищі;
- швидкість розповсюдження світла в даному середовищі; 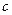 - швидкість розповсюдження світла у вакуумі, яка згідно сучасних уявлень, є найбільшою швидкістю, що відома в природі, вона приблизно дорівнює:
- швидкість розповсюдження світла у вакуумі, яка згідно сучасних уявлень, є найбільшою швидкістю, що відома в природі, вона приблизно дорівнює:  .
.
Дослід показує, що показник заломлення залежить від довжини хвилі. Залежність показника заломлення світла від довжини хвилі називається дисперсією. Дисперсія притаманна всім середовищам за винятком абсолютного вакууму і вона виникає внаслідок вимушених коливань заряджених частинок речовини – електронів та іонів під впливом змінного поля електромагнітної хвилі.
