Ентропія як параметр стану термодинамічної системи

Термін ентропія (від грец. entropia – міра перетворень ) введений у 1865 році Клаузіусом.

Поняття про ентропію будується на основі наступних розумінь.

Рівняння 1-го закону ТТД, як відомо має вид: 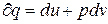чи

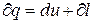
У цьому рівнянні 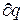не є повним диференціалом, оскільки в праву частину рівняння входить член 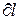, який не є повним диференціалом, тому що робота є не параметром стану газу, а функцією процесу (тобто щоб проінтегрувати праву частину цього вираження потрібно знати залежність р від v, тобто процес, який робить газ). Унаслідок цього, рівняння не можна проінтегрувати в інтервалі двох довільно обраних станів газу.

Як відомо з математики, усякий двочлен можна представити у виді повного диференціала, якщо його помножити на так званий інтегруючий множник. Таким інтегруючим множником для елементарної кількості теплоти 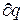є 1/Т, тобто одержуємо:

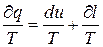, (3.19)

Рівняння (3.19) можна представити в іншому виді:

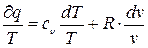, так як 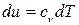а р/Т=R/v , (3.20)

Вираження (3.20) говорить про те, що 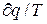являє собою повний диференціал деякої функції S (тобто 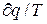=S) є параметром стану газу, оскільки вона залежить тільки від двох параметрів газу і тому не залежить від того яким шляхом газ з одного стану перейшов в інший. Цей параметр стану газу зветься ентропією газу і позначається через S і має розмірність Дж/К.

Ентропію, віднесену до 1 кг газу звуть питомою ентропією газу, позначається s і виміряється в Дж/кг К.

Проінтегрував обидві частини рівності (3.20) по будь-якому шляху переходу зі стану 1 у стан 2, одержимо: 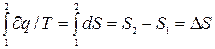, (3.21)

Зі сказаного випливає, що ентропія є функція будь-якої пари параметрів стану:

S = f1 (p,T); S = f2 ( 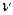,T); S = f3 (p, 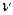); S = f4 (u, 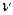); S = f5 (h, T); і т.д.

Таким чином ентропію можна визначити із рівнянь I-го закону ТТД.

;

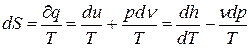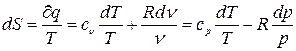
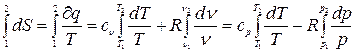
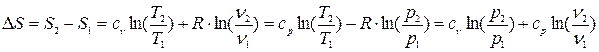,(3.22)

В оборотних процесах dS і 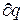мають однаковий знак, тому що Т має тільки позитивний знак. Тоді при підведенні теплоти до робочого тіла 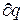> 0 ентропія збільшується, при відводі теплоти 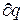< 0 - ентропія зменшується, у процесі без відводу і підведення теплоти 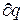= 0 (адіабатний процес) ентропія залишається постійної dS = 0.

Таким чином по характеру зміни ентропії можна судити про напрямок процесу переносу теплоти.

З (3.21) випливає, що кількість теплоти, яка брала участь у тім чи іншому ТД процесі при зміні стану робочого тіла від стану 1 до стану 2 можна виразити таким чином:

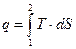, (3.23)

Теплова T, S – діаграма

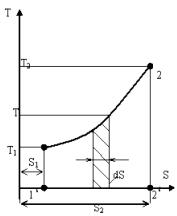
Поняття ентропії дозволяє ввести надзвичайно зручну для ТД розрахунків T,S – діаграму, на якій (як і на p, v – діаграмі) стан ТД системи зображується крапкою, а рівноважний ТД процес – лінією, мал.3.3.

Любий оборотний ТД процес, зображений у p, v – діаграмі, може бути перенесений у T, S – діаграму. Для цього треба знати рівняння процесу f (p, v)=0 і залежність S=f (p, v) ентропії від параметрів стану p і v.

Для відшукання крапки процесу на діаграмі по рівнянню стану і відомих значеннях v і p визначають температуру Т та значення ентропії S.

T, S – діаграма дає представлення про кількість теплоти, підведеної чи відведеної до робочого тіла в процесі у виді площі під процесом (пл.1-2-2 -1 ). Це випливає з рівняння .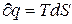

По T, S – діаграмі можна судити також про напрямок теплообміну між джерелом теплоти і робочим тілом.

Як вже відзначалося, напрямок теплового потоку повинний збігатися з алгебраїчним знаком dS, тому що абсолютна температура Т – завжди позитивна величина. Таким чином, оборотний процес зі збільшенням ентропії йде з підведенням

Мал.3.3 теплоти, а оборотний процес зі зменшенням ентропії йде з відводом теплоти від робочого тіла.

Рівняння Майєра

Відповідно до 1-го закону ТТД для закритих систем маємо: 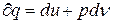, (3.24)

З урахуванням співвідношення (3.4.а) і (3.24) маємо:

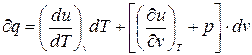, (3.25)

Для ізохорного процесу (v = const) це рівняння приймає вид:

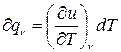, з огляду на те, що 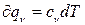, одержимо:

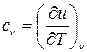, (3.26)

т.ч. ізохорна теплоємність тіла дорівнює частинної похідної від його внутрішньої енергії по температурі і характеризує темп росту внутрішньої енергії в ізохорному процесі з ростом температури.

Для ізобарного процесу (p=const) з рівняння (3.25) і 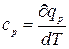одержуємо (підставляючи значення 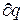з рівняння (3.25) у вираження :

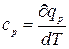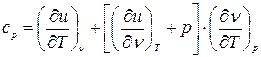, (3.27) 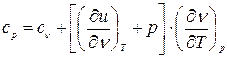, (3.28)

Це рівняння показує зв'язок між 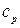і 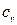. Для ідеального газу воно значно спрощується. Дійсно, внутрішня енергія ідеального газу визначається тільки його температурою і не залежить від об’єму, тому 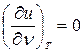і крім того, з рівняння Клапейрона випливає: 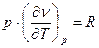відкіля 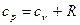, (3.29)

Це співвідношення зветься рівнянням Майєра і є одним з основних у ТТД.

Множачи всі члени рівняння (3.29) на молекулярну масу 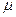в результаті одержимо:

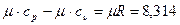кДж/кмоль К, (3.30)

З цього рівняння видно, що для ідеальних газів різниця мольних теплоємкостей є величина постійна, рівна універсальній газовій постійній.

ЛЕКЦІЯ 4