Свойства частиц и взаимодействий 3 страница
где Eсв(A, Z) и Eсв(A, Z-1) - энергии связи исходного и конечного ядер; mn, mp и me - массы нейтрона, протона и электрона.
Qe = Eсв( 7Li) - Eсв( 7Be) - 0.78 МэВ = (39.3 - 37.6 - 0.78) МэВ ~ 0,9 МэВ.
Из законов сохранения энергии и импульса следует
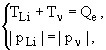
где TLi, 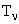 - кинетические энергии отдачи ядра и нейтрино. Нейтрино - релятивистская частица, а ядро - нерелятивистское:
- кинетические энергии отдачи ядра и нейтрино. Нейтрино - релятивистская частица, а ядро - нерелятивистское:
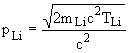 ;
; 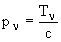 ;
;
Окончательно имеем
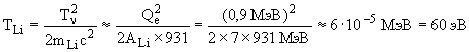 .
.
11. Определить кинетическую энергию конечного ядра при  --распаде ядра 64Cu (64Cu
--распаде ядра 64Cu (64Cu  64Zn + e +
64Zn + e +  e) когда
e) когда
1) энергия антинейтрино 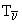 = 0, 2) энергия электрона Te = 0. Энергии связи ядер 64Cu - 559.32 Мэв и 64Zn - 559.12 МэВ.
= 0, 2) энергия электрона Te = 0. Энергии связи ядер 64Cu - 559.32 Мэв и 64Zn - 559.12 МэВ.
Энергия  -- распада
-- распада
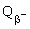 = Eсв(A,Z+1) - Eсв(A, Z) + (mn - mp)c2 - mec2 = Eсв(A,Z+1) - Eсв(A,Z) + 0.78 МэВ = 0.58 МэВ,
= Eсв(A,Z+1) - Eсв(A, Z) + (mn - mp)c2 - mec2 = Eсв(A,Z+1) - Eсв(A,Z) + 0.78 МэВ = 0.58 МэВ,
где Eсв(A, Z) и Eсв(A, Z + 1) - энергии связи исходного и конечного ядер; mn, mp и me - массы нейтрона, протона и электрона. Энергия отдачи ядра при  -- распаде будет:
-- распаде будет:
1) 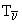 = 0. Запишем законы сохранения энергии и импульса
= 0. Запишем законы сохранения энергии и импульса
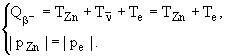
Для импульсов, учитывая, что pZn - нерелятивистский импульс, pe - релятивистский импульс, можно записать 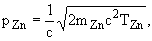
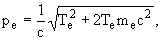
где mZn - масса ядра 64Zn. Из законов сохранения имеем
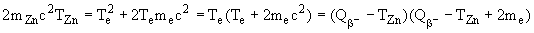 .
.
Далее, т.к. me << mZn, то TZn << 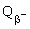
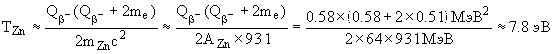 .
.
2) Te = 0. Аналогично как и в первом случае
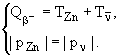
Импульс антинейтрино ультрарелятивистский
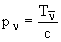 .
.
Окончательно получим
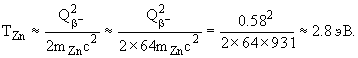 .
.
12. Даны избытки масс атомов -
 (114Cd) = -90.021 МэВ,
(114Cd) = -90.021 МэВ,  (114In) = -88.379 МэВ и
(114In) = -88.379 МэВ и  (114Sn) = -90.558 МэВ.
(114Sn) = -90.558 МэВ.
Определить возможные виды  -распада ядра 114In.
-распада ядра 114In.
Для ядра 114In b - распады выглядят так:
 --распад - 114In --распад - 114In  114Sn + e- + 114Sn + e- +  e, e, |
 +-распад - 114In +-распад - 114In  114Cd + e+ + 114Cd + e+ +  e, e, |
e- захват - 114In + e-  114Cd + 114Cd +  e. e. |
Если величина энергии распада положительна, то ядро неустойчиво к распаду этого типа.
Энергии распадов:
 --распад - --распад - | 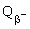 = =  (A,Z) - (A,Z) -  (A,Z+1); (A,Z+1); |
 +-распад - +-распад - | 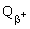 = =  (A,Z) - (A,Z) -  (A,Z-1) - 2meс2; (A,Z-1) - 2meс2; |
| e- захват - | Qe =  (A,Z) - (A,Z) -  (A,Z-1); (A,Z-1); |
где  (A, Z) - избыток масс исходного ядра,
(A, Z) - избыток масс исходного ядра,  (A, Z + 1) и
(A, Z + 1) и  (A, Z - 1) - избытки масс конечных ядер, me - масса электрона. Подставим значения:
(A, Z - 1) - избытки масс конечных ядер, me - масса электрона. Подставим значения:
 --распад - --распад - | 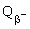 = 90.558 - 88.379 = 2.179 МэВ > 0; = 90.558 - 88.379 = 2.179 МэВ > 0; |
 +-распад - +-распад - | 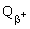 = 90.021 - 88.379 - 1.022 = 0.62 МэВ > 0; = 90.021 - 88.379 - 1.022 = 0.62 МэВ > 0; |
| e- захват - | Qe = 90.021 - 88.379 = 1.642 МэВ > 0; |
Таким образом, ядро 114In испытывает все три вида  - распада.
- распада.
13. Показать, что в случае  -распада 42Sc имеет место разрешенный переход типа Ферми, а 32P - типа Гамова-Теллера.
-распада 42Sc имеет место разрешенный переход типа Ферми, а 32P - типа Гамова-Теллера.
К разрешенным  -переходам относятся переходы, при которых суммарный орбитальный момент l, уносимый электроном и нейтрино, равен нулю. Разрешенные переходы делятся на переходы типа Ферми, при которых спины электрона и нейтрино антипараллельны, и типа Гамова-Теллера, при которых спины электрона и нейтрино параллельны. Для разрешенных
-переходам относятся переходы, при которых суммарный орбитальный момент l, уносимый электроном и нейтрино, равен нулю. Разрешенные переходы делятся на переходы типа Ферми, при которых спины электрона и нейтрино антипараллельны, и типа Гамова-Теллера, при которых спины электрона и нейтрино параллельны. Для разрешенных  -переходов справедливы соотношения
-переходов справедливы соотношения
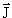 i +
i + 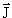 j = 0, Pi = Pf для переходов Ферми,
j = 0, Pi = Pf для переходов Ферми,
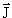 i +
i + 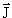 j = 0, 1 (кроме 0
j = 0, 1 (кроме 0  0 переходов), Pi = Pf для переходов Гамова-Теллера, i и f обозначают начальное и конечное ядро.
0 переходов), Pi = Pf для переходов Гамова-Теллера, i и f обозначают начальное и конечное ядро.
Рассмотрим переход 42Sc (0+)  42Ca (0+): для него Pi = Pf и
42Ca (0+): для него Pi = Pf и 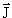 i +
i + 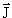 j = 0, то есть выполнены все условия для перехода типа Ферми.
j = 0, то есть выполнены все условия для перехода типа Ферми.
Рассмотрим переход 32P (1+)  32Sc (0+): для него Pi = Pf и
32Sc (0+): для него Pi = Pf и 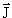 i +
i + 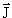 j = 1, то есть все условия для перехода типа Гамова-Теллера выполнены.
j = 1, то есть все условия для перехода типа Гамова-Теллера выполнены.
14. Определить порядок запрета следующих  -переходов:
-переходов:
- 89Sr(5/2+)
 89Y(1/2-);
89Y(1/2-); - 36Cl(2+)
 36Ar(0+);
36Ar(0+); - 137Cs(7/2+)
 137Ba(3/2+).
137Ba(3/2+).
Запрещенные переходы подразделяются по порядку запрета, который определяется суммарным орбитальным моментом l, уносимым электроном и нейтрино. Если l = 1, то это запрещенный переход первого порядка, l = 2 - второго порядка и т.д. Справедливы следующие соотношения:
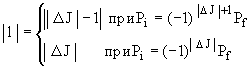 .
.
- 89Sr(5/2+)
 89Y(1/2-) - возможны два варианта:
89Y(1/2-) - возможны два варианта:
 J = 2; l = 1; Pi = (-1)3 Pf - первого порядка запрета и
J = 2; l = 1; Pi = (-1)3 Pf - первого порядка запрета и
 J = 3; l = 3; Pi = (-1)3 Pf - третьего порядка запрета.
J = 3; l = 3; Pi = (-1)3 Pf - третьего порядка запрета.
Так как вероятность -переходов сильно падает при увеличении порядка запрета, то в данном случае будет преобладать
-переходов сильно падает при увеличении порядка запрета, то в данном случае будет преобладать  -переход первого порядка запрета.
-переход первого порядка запрета. - 36Cl(2+)
 36Ar(0+) - возможен всего один вариант:
36Ar(0+) - возможен всего один вариант:
 J = 2; l = 2; Pi = (-1)2 Pf - это
J = 2; l = 2; Pi = (-1)2 Pf - это  -переход второго порядка запрета.
-переход второго порядка запрета. - 137Cs(7/2+)
 137Ba(3/2+) - возможны два варианта:
137Ba(3/2+) - возможны два варианта:
 J = 2, 3; l = 2; Pi = (-1)2,4 Pf -
J = 2, 3; l = 2; Pi = (-1)2,4 Pf -  -переход второго порядка запрета и
-переход второго порядка запрета и
 J = 4, 5; l = 4; Pi = (-1)4,6 Pf - это b -переход четвертого порядка запрета.
J = 4, 5; l = 4; Pi = (-1)4,6 Pf - это b -переход четвертого порядка запрета.
Преобладающим будет -переход второго порядка.
-переход второго порядка.
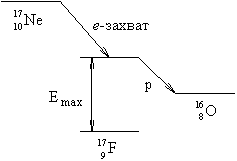 15. Для ядра 17Ne определить максимальную энергию запаздывающих протонов, вылетающих из ядра 17F, образующегося в результате e-захвата на ядре 17Ne. Энергии связи Eсв(17Ne) = 112.91 МэВ, Eсв(17F) = 128.23 МэВ и Eсв(16O)=126.63 МэВ.
15. Для ядра 17Ne определить максимальную энергию запаздывающих протонов, вылетающих из ядра 17F, образующегося в результате e-захвата на ядре 17Ne. Энергии связи Eсв(17Ne) = 112.91 МэВ, Eсв(17F) = 128.23 МэВ и Eсв(16O)=126.63 МэВ.
Рассматриваемый процесс 17Ne + e-  17F* +
17F* +  e
e  16O + p. Максимальная энергия возбуждения ядра 17F* равна энергии e-захвата
16O + p. Максимальная энергия возбуждения ядра 17F* равна энергии e-захвата
Emax(17F*) = Qe = Eсв(17F) - Eсв.(17Ne) - 0.78 МэВ = 128.23 МэВ - 112.91 МэВ = 14.54 МэВ.
Энергия отделения протона для ядра 17F
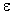 p = Eсв(A, Z) - Eсв(A-1, Z-1) = Eсв(17F) - Eсв(16O) = 128.23 МэВ - 126.63 МэВ = 1.6 МэВ.
p = Eсв(A, Z) - Eсв(A-1, Z-1) = Eсв(17F) - Eсв(16O) = 128.23 МэВ - 126.63 МэВ = 1.6 МэВ.
Максимальная энергия запаздывающих протонов 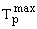 есть
есть
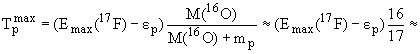
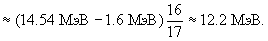
16. Определить типы и мультипольности  -переходов:
-переходов:
| 1) | 1-  0+, 0+, | 4) | 2+  3-, 3-, |
| 2) | 1+  0+, 0+, | 5) | 2+  3+, 3+, |
| 3) | 2-  0+, 0+, | 6) | 2+  2+. 2+. |
Изменения состояний атомных ядер, сопровождающиеся испусканием или поглощением квантов электромагнитного поля, называются  -переходами. Полный момент количества движения фотона J называется его мультипольностью. Значение спина фотона Jmin= 1. Полный момент J может принимать только целочисленные значения (кроме нуля).
-переходами. Полный момент количества движения фотона J называется его мультипольностью. Значение спина фотона Jmin= 1. Полный момент J может принимать только целочисленные значения (кроме нуля).
Различаются переходы электрические (EJ) и магнитные (MJ). Для электрических фотонов четность P = (-1)J. Для магнитных фотонов P = (-1)J+1.
- 1-
 0+ - J = 1; P = -1, фотоны типа E1;
0+ - J = 1; P = -1, фотоны типа E1; - 1+
 0+ - J = 1; P = +1, фотоны типа M1;
0+ - J = 1; P = +1, фотоны типа M1; - 2-
 0+ - J = 2; P = -1, фотоны типа M2;
0+ - J = 2; P = -1, фотоны типа M2; - 2+
 3- - J = 1, 2, 3, 4, 5; P = -1, фотоны типа E1, M2, E3, M4, E5; преобладают фотоны типа E1;
3- - J = 1, 2, 3, 4, 5; P = -1, фотоны типа E1, M2, E3, M4, E5; преобладают фотоны типа E1; - 2+
 3+ - J = 1, 2, 3, 4, 5; P = +1, фотоны типа M1, E2, M3, E4, M5; преобладают фотоны типа M1 и E2;
3+ - J = 1, 2, 3, 4, 5; P = +1, фотоны типа M1, E2, M3, E4, M5; преобладают фотоны типа M1 и E2; - 2+
 2+ - J = 1, 2, 3, 4; P = +1, фотоны типа M1, E2, M3, E4; преобладают фотоны типа M1 и E2.
2+ - J = 1, 2, 3, 4; P = +1, фотоны типа M1, E2, M3, E4; преобладают фотоны типа M1 и E2.
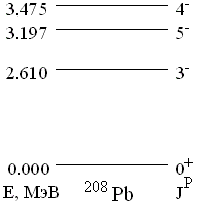 17. По схеме низших возбужденных состояний ядра 208Pb определить наиболее вероятный путь распада возбужденного состояния 4- с энергией 3.475 МэВ. Указать мультипольности переходов.
17. По схеме низших возбужденных состояний ядра 208Pb определить наиболее вероятный путь распада возбужденного состояния 4- с энергией 3.475 МэВ. Указать мультипольности переходов.
Период полураспада T1/2  -переходов зависит от мультипольности перехода J и длины волны излучения
-переходов зависит от мультипольности перехода J и длины волны излучения 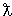 .
.
| Для электрических переходов EJ - | 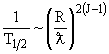 , , |
| для магнитных переходов MJ - | 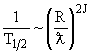 , , |
где R - радиус ядра.
Рассмотрим переходы с уровня E(JP = 4-) = 3.475 МэВ:
· переход (4-  5- ) имеет J = 1, 2, 3, 4, 5, 6, 7, 8, 9; Pi / Pf = +1 и типы переходов M1 + E2 + M3 + E4 + M5 + E6 + M7 + E8 + M9; распад происходит в основном с излучением фотонов типа M1 + E2;
5- ) имеет J = 1, 2, 3, 4, 5, 6, 7, 8, 9; Pi / Pf = +1 и типы переходов M1 + E2 + M3 + E4 + M5 + E6 + M7 + E8 + M9; распад происходит в основном с излучением фотонов типа M1 + E2;
· переход (4-  3- ) имеет J = 1, 2, 3, 4, 5, 6, 7; Pi / Pf = +1 и типы переходов M1 + E2 + M3 + E4 + M5 + E6 + M7; распад происходит в основном с излучением фотонов типа M1 + E2;
3- ) имеет J = 1, 2, 3, 4, 5, 6, 7; Pi / Pf = +1 и типы переходов M1 + E2 + M3 + E4 + M5 + E6 + M7; распад происходит в основном с излучением фотонов типа M1 + E2;
· переход (4-  0+) имеет J = 4; Pi / Pf = - 1 и тип перехода M4.
0+) имеет J = 4; Pi / Pf = - 1 и тип перехода M4.
Наибольшую вероятность имеют переходы с наименьшей мультипольностью, в данном случае это (4-  5- ) и (4-
5- ) и (4-  3- ). Из этих двух переходов большую вероятность имеет переход (4-
3- ). Из этих двух переходов большую вероятность имеет переход (4-  3- ), так как энергия этого перехода
3- ), так как энергия этого перехода
E (4-  3-) = 3.475 - 2.610 = 0.865 МэВ больше энергии перехода
3-) = 3.475 - 2.610 = 0.865 МэВ больше энергии перехода
E (4-  5-) = 3.475 - 3.197 = 0.278 МэВ, и, соответственно, длина волны
5-) = 3.475 - 3.197 = 0.278 МэВ, и, соответственно, длина волны 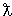 излучения, входящая в знаменатель выражения для вероятности перехода, меньше.
излучения, входящая в знаменатель выражения для вероятности перехода, меньше.
Таким образом, распад возбужденного состояния ядра 208Pb с E(JP = 4- ) = 3.475 МэВ происходит в основном по каналу (4-  3-
3-  0+).
0+).
18. Согласно классической электродинамике, электрический диполь размера l в единицу времени излучает энергию, определяемую соотношением
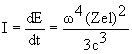 ,
,
где w - циклическая частота колебаний диполя, Ze и l - заряд и размер диполя. Используя это соотношение, оценить среднее время для электрических дипольных переходов  -квантов с энергией 1 МэВ в ядре A
-квантов с энергией 1 МэВ в ядре A 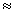 70.
70.
Предположим, что для ядра с массовым числом A=70 зарядовое число Z=30 и определим радиус диполя равным радиусу ядра - R = r0A1/3, где величина r0 = 1.2 Фм. Число  -квантов в единицу времени N, учитывая, что
-квантов в единицу времени N, учитывая, что 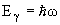 :
:
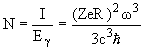 .
.
Оценим среднее время жизни:
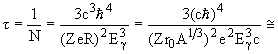
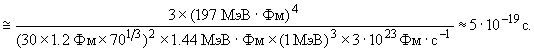
19. Оценить допплеровское уширение спектральной линии с энергией 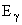 = 1 МэВ при комнатной температуре (T = 300 K).
= 1 МэВ при комнатной температуре (T = 300 K).
Допплеровское уширение спектральной линии
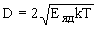 ,
,
где T - температура в абсолютной шкале, k - постоянная Больцмана. Энергия отдачи ядра при испускании  -кванта
-кванта
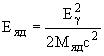 .
.
Предположим, что масовое число ядра A = 50. Учитывая, что для комнатной температуры T = 300 K величина kT = 0.025 эВ, получаем
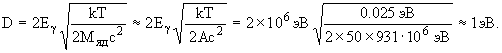
20. Используя формулу Вайцзеккера, получить соотношение для вычисления энергии спонтанного деления на два одинаковых осколка и рассчитать энергию симметричного деления ядра 238U.
Энергия деления ядра на два одинаковых осколка Qf = (mисх - 2mоск) = 2Wоск - Wисх, где mисх и mоск - массы исходного ядра и каждого из осколков, а Wисх и Wоск - их энергии связи. Формула Вайцзеккера для энергии связи ядра
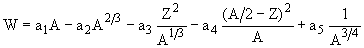 ,
,
где a1 = 15.78 МэВ, a2 = 17.8 МэВ, a3 = 0.71 МэВ, a4 = 94.8 МэВ, a5 = 0 для ядер с нечетным A, a5 = +34 МэВ для четно- четных ядер и a5 = - 34 МэВ для нечетно- нечетных ядер. Последний член a5/A3/4 вследствие его малости рассматривать не будем.
При делении исходного ядра (Aисх, Zисх) на два одинаковых осколка (Aоск, Zоск) их массовые числа и заряды имеют следующие соотношения: Aоск = Aисх/2 и Zоск = Zисх/2. Энергия деления ядра будет зависеть только от второго и третьего членов формулы Вайцзеккера - поверхностной и кулоновской энергии:
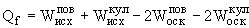
Поверхностная энергия осколков
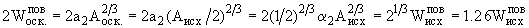 .
.
Кулоновская энергия осколков
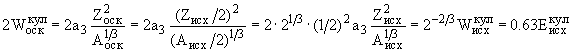 .
.
Энергия деления ядра Qf выделяется в результате изменения кулоновской и поверхностной энергии исходного ядра и осколков
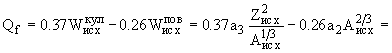
Свойства частиц и взаимодействий
Ядерные реакции
1.Перечислить несколько ядерных реакций, в которых может образоваться изотоп 8Be.

Используя закон сохранения заряда и закон сохранения числа нуклонов, получим
1.  + +   8Be + 8Be +  , , | 5.  + 10Be + 10Be  8Be + d, 8Be + d, |
2. d + 6Li  8Be + 8Be +  , , | 6. p + 10B  8Be + 3He, 8Be + 3He, |
3. p + 7Li  8Be + 8Be +  , , | 7. p + 11B  8Be + 8Be +  , , |
4.  + 9Be + 9Be  8Be + n, 8Be + n, | 8. p + 10B  8Be + 8Be +  . . |
2.Какую минимальную кинетическую энергию в лабораторной системе Tmin должен иметь нейтрон, чтобы стала возможной реакция 16O(n,  )13C?
)13C?

Минимальная энергия, при которой возможна реакция, равна порогу реакции. Вычислим энергию реакции:
Q=8.071 - 4.737 - 2.424 -3.125 = -2.215 МэВ
Для вычисления пороговой энергии Tпор используем нерелятивистское приближение (2.14a):
Tmin = Tпор = 2.215(1 + 1/17) = 2.35 МэВ.
3. Является ли реакция 6Li(d,  )4He эндотермической или экзотермической? Даны удельные энергии связи ядер в МэВ:
)4He эндотермической или экзотермической? Даны удельные энергии связи ядер в МэВ: 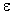 (d) = 1.11;
(d) = 1.11; 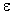 (
(  ) = 7.08;
) = 7.08; 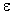 (6Li) = 5.33.
(6Li) = 5.33.
