Задача молекулярно-кінетичної теорії полягає в тому, щоб встановити зв'язок між мікроскопічними і макроскопічними параметрами.

Використовуючи модель ідеального газу, обчислимо тиск газу на стінку посудини. Тиск виникає внаслідок ударів молекул о стінки посудини. Визначається тиск силою, з якою діє газ на одиницю площі поверхні стінки і яка напрямлена перпендикулярно поверхні 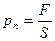. Щоб знайти тиск газу, потрібно знайти, який імпульс передає газ одиниці площі стінки посудини в секунду. Будемо вважати, що зіткнення окремої молекули зі стінкою посудини підкоряється законам пружного зіткнення: молекула відскакує від стінки з початковим за модулем імпульсом, а кут її падіння дорівнює куту відбивання. При цьому проекція швидкості молекули перпендикулярна стінці змінює свій знак на протилежний, але залишається постійною за модулем; проекція швидкостіпаралельна стінці залишається незмінною (рис.1).

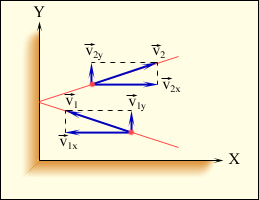Рисунок 1 - Пружне зіткнення молекули зі стінкою

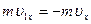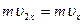Тому в результаті зіткнень молекули зі стінкою проекція її імпульсу на вісь OX змінюється від до . Зміна імпульсу молекули буде дорівнювати 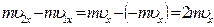, де m – маса молекули.

Виділимо деяку площадку S (рис.2). За час Δt з цією площадкою зіштовхнуться всі молекули, що мають проекцію швидкості υ_x, спрямовану убік стінки, і що знаходяться в циліндрі з площею основи S і висотою υ_xΔt.

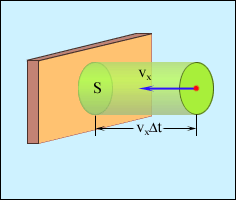Рисунок 2 - Визначення числа зіткнень молекул із площадкою S

Припустимо, що газ знаходиться в стані рівноваги, тобто газ як одне ціле покоїться відносно стінок посудини, а число молекул, що рухаються в довільному напрямку дорівнює числу молекул, що рухаються в протилежну сторону. Нехай в одиниці об'єму посудини міститься n молекул; тоді число молекул в об'ємі циліндра дорівнює nSυ_xΔt. Але з них лише половина рухається до стінки. Інша половина рухається від неї.Отже, число ударів молекул об площадку S за час Δt дорівнює 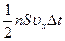. Оскільки кожна молекула при зіткненні зі стінкою змінює свій імпульс на величину 2mυ_x, то повна зміна імпульсу всіх молекул, що зіштовхнулися за час Δt із площадкою S, дорівнює 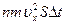. За законами механіки ця зміна імпульсу всіх молекул, що зіштовхнулися зі стінкою, відбувається піддією імпульсу сили F_хDt, де F_х – деяка середня сила, що діє на молекули з боку стінки площадці S. Але за 3-м законом Ньютона така ж по модулю сила діє з боку молекул на площадку S. Тому можна записати:

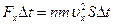(1)

Розділивши обидві частини на SΔt, одержимо:

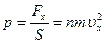(2)

де p – тиск газу на стінку посудини, який дорівнює відношенню нормальної компоненти сили до одиниці площі поверхні.

При виведенні цього співвідношення передбачалося, що всі n молекул, які містяться в одиниці об'єму газу, мають однакові проекції швидкостей на вісь X. Насправді це не так. Врахуємо різницю швидкостей молекул та їх проекцій на вісі координат тим, що замінимо величину 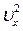, що входить у формулу (2), її середнім значенням .

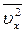Оскільки всі напрямки для векторів швидкостей молекул рівноймовірні, середнє значення квадратів їх проекцій на координатні осі рівні між собою (газ ізотропний):

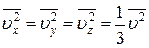(6)

Остання рівність випливає з формули:

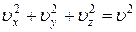
Формула для середнього тиску газу на стінку посудини запишеться у вигляді

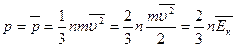(7)

Величина 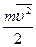в формулі (7) являє собою середню кінетичну енергію однієї молекули газу. Рівняння (7) встановлює зв'язок між тиском p ідеального газу, масою молекули m, концентрацією молекул n, середнім значенням квадрата швидкості 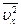і середньою кінетичною енергією 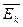поступального руху молекул. Його називають основним рівнянням молекулярно-кінетичної теорії газів.

Таким чином, тиск газу дорівнює двом третинам середньої кінетичної енергії поступального руху молекул, що містяться в одиниці об'єму.

Температура

В основне рівняння молекулярно-кінетичної теорії газів входить добуток концентрації молекул n на середню кінетичну енергію 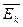поступального руху. Якщо газ знаходиться в посудині незмінного об’єму V, то концентрація 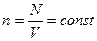(де N – число молекул у посудині). У цьому випадку зміна тиску Δp пропорційна зміні середньої кінетичної енергії .

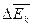Виникає питання: яким чином можна змінювати середню кінетичну енергію руху молекул у посудині незмінного об’єму? Яку фізичну величину потрібно змінити, щоб змінилася середня кінетична енергія 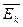. З досліду відомо, що за умов постійного об’єму тиск газу, і відповідно 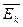, можна змінювати тільки одним способом: його нагріванням чи охолодженням; при нагріванні газу його тиск зростає, при охолодженні – зменшується. Отже, між температурою і середньою кінетичною енергією молекул повинен існувати зв’язок.

Стосовно до ідеального газу, зручно казати, що температура дорівнює двом третинам кінетичної енергії молекул, тому що це спрощує вигляд формули (7) для тиску газу:

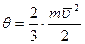
Тоді рівняння (7) набуває вигляду:

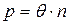
Визначену таким чином температуру q - називають енергетичною температурою. В системі СІ енергетична температура q вимірюється в джоулях. На практиці абсолютна температура вимірюється в кельвінах (К). Кількість джоулів, що відповідає одному кельвінові, - перехідний множник від градуса до джоуля - позначається буквою k і називається сталою Больцмана. Таким чином,

,

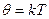p =qn= nkT (8)

Стала Больцмана – одна з фундаментальних фізичних констант. Її чисельне значення в СІ дорівнює:

k = 1,38·10^–23 Дж/К.

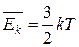(9)

Середня кінетична енергія хаотичного руху молекул газу прямо пропорційна абсолютній температурі.

Таким чином, з молекулярно-кінетичної точки зору, температура є мірою середньої кінетичної енергії поступального руху молекул.

Варто звернути увагу на те, що середня кінетична енергія поступального руху молекули не залежить від її маси. Броунівська частка, зважена в рідині або газі, має таку ж середню кінетичну енергію, як і окрема молекула, маса якої на багато порядків менше маси броунівської частки.