Основы фильтрации в частотной области

Каждый элемент фурье-образа 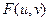содержит все отсчеты функции 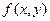. Поэтому обычно, за исключением тривиальных случаев, невозможно установить прямое соответствие между характерными деталями изображения и его фурье-образа. Однако некоторые общие утверждения относительно взаимосвязи частотных составляющих фурье-образа и пространственных характеристик изображения могут быть сделаны. Частоты в фурье-преобразовании связаны с вариацией яркости на изображении. Наиболее медленно меняющаяся (постоянная) частотная составляющая (u=v=0) совпадает со средней яркостью изображения. Низкие частоты, отвечающие точкам вблизи начала координат фурье-преобразования, соответствуют медленно меняющимся компонентам изображения. На изображении комнаты, например, они могут соответствовать плавным изменениям яркости стен и пола. По мере удаления от начала координат, более высокие частоты начинают соответствовать все более и более быстрым изменениям яркости, которые суть границы объектов (контуры) и другие детали изображения, характеризуемые резкими изменениями яркости, такие как шум.

Один из часто используемых способов обработки изображения, которая выполняется с различными целями, является частотная фильтрация.

Процедура фильтрации в частотной области состоит из следующих шагов (рис.1.7):

1. Исходное изображение умножается на 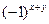, чтобы его преобразование Фурье оказалось центрированным.

2. Вычисляется прямое ДПФ 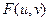изображения, полученного после шага 1.

3. Функция 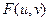умножается на функцию фильтра .

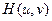4. Вычисляется обратное ДПФ от результата шага 3.

5. Выделяется вещественная часть результата шага 4.

6. Результат шага 5 умножается на .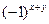

Пусть 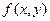обозначает входное изображение после шага 1, 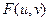- его фурье-образ. Тогда фурье-образ выходного изображения определяется выражением:

.

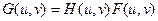Умножение функций двух переменных 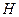и 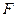осуществляется поэлементно, т.е. первый элемент функции 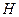умножается на первый элемент функции 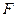, второй элемент функции 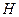умножается на второй элемент функции 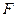и т.д. В общем случае компоненты фильтра 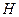являются комплексными величинами. На практике чаще всего используются 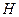с действительными компонентами. В этом случае и действительная и мнимая части функции 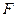умножаются на одну и ту же действительную функцию фильтра 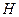. Такие фильтры называются фильтрами нулевого фазового сдвига, поскольку не меняют фазу фурье-преобразования.

Фильтрованное изображение получается вычислением обратного преобразования Фурье от фурье-образа :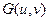

Фильтрованное изображение = F^-1 .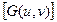

Искомое изображение получается выделением действительной части из последнего результата и умножения на 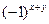, чтобы скомпенсировать эффект от умножения входного изображения на ту же величину. Обратное фурье-преобразование в общем случае является комплексным. Однако в случае вещественного входного изображения и вещественной функции фильтра мнимые части всех значений обратного фурье-преобразования должны равняться 0. Но на практике значения обратного фурье-преобразования, как правило, содержат паразитную мнимую составляющую, что связано с ошибками округлений при вычислениях. Этой составляющей необходимо пренебречь.

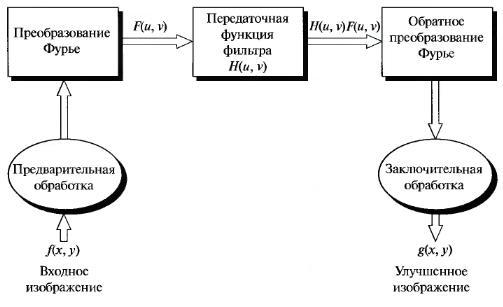
Рис.1.7. Основные этапы фильтрации в частотной области