Приложение В – Основные свойства и теоремы

Введение

В современных системах управления наряду с непрерывными способами передачи и преобразования сигналов широко применятся дискретные способы, в которых используется в том или ином виде дискретизация сигнала. Дискретизация состоит в замене непрерывного сигнала его дискретными значениями и может быть осуществлена по времени, по уровню, по времени и уровню. В импульсных системах хотя бы одна из величин, характеризующих состояние системы, квантуется по времени. В цифровых системах используется квантование по времени и уровню.

Область применения дискретных систем в настоящее время очень разнообразна. Можно выделить две категории таких систем:

- системы дискретные по своей природе (например, радиолокационные системы обнаружения и сопровождения цели);

- системы, в которых информация существует непрерывно, но намеренно квантуется для получения новых свойств, которые не могут быть получены в непрерывных системах, таких как повышенные точность, помехоустойчивость, быстродействие, простота реализации алгоритмов управления и др.).

Современные системы управления почти всегда снабжаются цифровым компьютером. Компьютеры работают с последовательностью чисел, а не с непрерывными функциями времени. Чтобы соединить аналоговый объект с компьютером, нужно преобразовать непрерывную функцию в последовательность чисел (произвести квантование) с последующим восстановлением непрерывного сигнала по последовательности чисел.

Чтобы понять, как работают такие системы, необходимо изучить эффекты, связанные с квантованием непрерывного сигнала.

Между аналоговым и цифровым управлением есть существенные различия. При описании непрерывных систем используются непрерывные сигналы (функции непрерывного времени), дифференциальные уравнения, преобразование Лапласа. При описании дискретных систем управления используются дискретные по времени сигналы, разностные уравнения, Z-преобразование. Но наряду с отличием при анализе и синтезе дискретных систем имеется много общего. Как и при анализе непрерывных систем, при анализе дискретных систем используются передаточные функции, временные и частотные характеристики. Поэтому для усвоения необходимы знания и умения, приобретенные при изучении непрерывных систем управления.

Целью контрольной работы является практическое освоение методов получения математического описания импульсных и цифровых систем управления.

1 Теоретическая часть

1.1 Общие сведения об импульсных и цифровых системах управления

Системы, которые являются непрерывными, за исключением одной или нескольких операций квантования по времени, называются импульсными системами. В общем случае импульсная автоматическая система может быть представлена взаимодействующими между собой непрерывной (НЧ) и импульсной (ИЧ) частей (рисунок 1). Импульсная часть выполняет операции квантования по времени и восстановления данных.

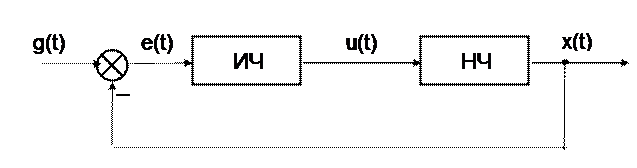
Рисунок 1 – Обобщенная функциональная схема импульсной автоматической системы управления

Импульсную часть можно рассматривать как некоторый преобразователь непрерывного сигнала e(t) в управляющее воздействие u(t). В простейшем случае импульсная часть является реальным импульсным элементом (РИЭ) (импульсным модулятором), на выходе которого формируется последовательность импульсов, зависящая от непрерывного сигнала ошибки. Например, при амплитудно-импульсной модуляции ИЧ преобразует непрерывный сигнал е(t) в последовательность импульсов, амплитуды которых пропорциональны значениям непрерывного сигнала ошибки в равноотстоящие моменты времени Т.

При анализе реальный импульсный элемент заменяют последовательным соединением идеального импульсного элемента (ИИЭ) (квантователя) и формирующего элемента (ФЭ) (фиксатора) (рисунок 2).

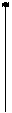
Рисунок 2 – Функциональная схема импульсной системы с идеальным импульсным элементом

Идеальный импульсный элемент под воздействием непрерывного сигнала e(t) формирует идеальные мгновенные импульсы вида δ-функций, «амплитуды площадей» которых равны значениям входного сигнала в моменты квантования nT, где n=0,1,2,…Т – период квантования.

Механизм квантования по времени иллюстрируется на рисунке 3. Квантователь (ИИЭ), представленный на рисунке 2 в виде ключа, можно рассматривать как импульсный модулятор с несущей в виде последовательности мгновенных единичных импульсов (рисунок 3,б)

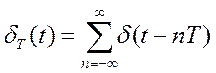(1)

и огибающей в виде входного непрерывного сигнала e(t) (рисунок 3,а), где

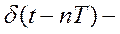
смещенная на время nΤ дельта-функция, площадь которой

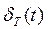равна единице. Функцию называют функцией единичных импульсов и широко используют при исследовании импульсных систем.

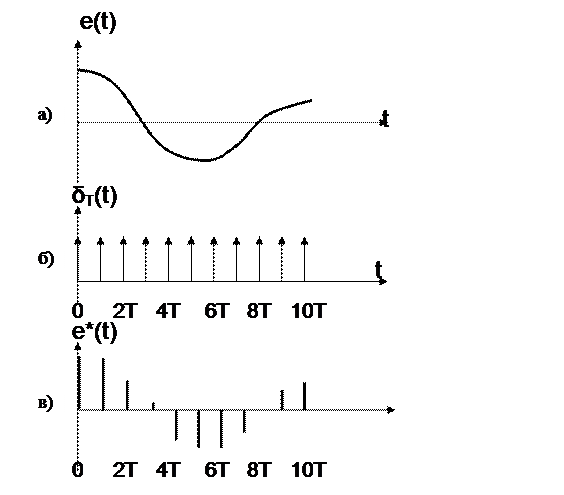
Рисунок 3 – Квантование сигнала по времени

Назначение ФЭ сводится к тому, чтобы преобразовать квантованный сигнал в форму, близкую исходному непрерывному сигналу.
Простейшим и наиболее распространенным устройством восстановления данных является фиксатор (экстраполятор) нулевого порядка. Передаточная функция фиксатора нулевого порядка

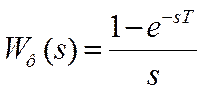. (2)

Выходной сигнал экстраполятора нулевого порядка u(t) в течение всего периода квантования сохраняет постоянное значение, равное значению исходного сигнала e(t) в момент квантования. Принцип действия цепи из последовательно соединенных идеального квантователя и фиксатора нулевого порядка показан на рисунке 4.

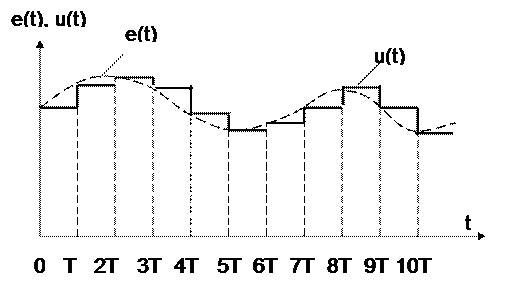
Рисунок 4 – Входной и выходной сигналы цепи квантователь/фиксатор

Необходимо отметить, что квантователь (ключ) не является моделью реального квантователя, а блок с передаточной функцией (2) не является моделью реального фиксатора. Однако комбинация этих элементов точно отражает соотношение между входом и выходом реального импульсного элемента (устройства выборки/хранения).

Для удобства анализа ФЭ и непрерывную часть импульсной системы объединяют, и эту объединенную часть называю приведенной непрерывной частью (ПНЧ) (рисунок 5).

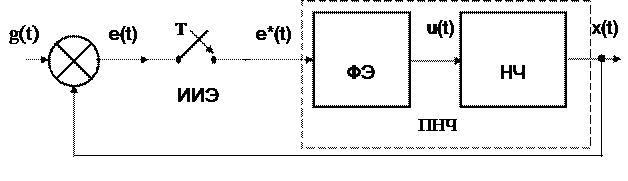
Рисунок 5 – Эквивалентная схема импульсной системы с амплитудно-импульсной модуляцией

Формирующий элемент и непрерывная часть соединены последовательно. Следовательно, передаточная функция приведенной непрерывной части равна

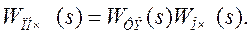(3)

В цифровых системах управления (рисунок 6) непрерывный сигнал квантуется по времени и по уровню.

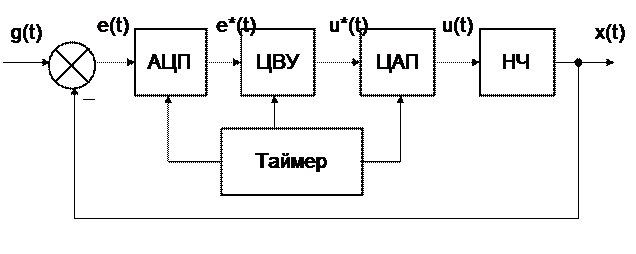
Рисунок 6 – Функциональная схема цифровой системы управления

Аналого-цифровой преобразователь (АЦП) преобразует непрерывный сигнал е(t) в цифровой. Цифровое вычислительное устройство (ЦВУ) выполняет все необходимые вычисления в соответствии с заданным алгоритмом управления. Цифро-аналоговый преобразователь (ЦАП) преобразует цифровое управляющее воздействие u*(t) в непрерывный сигнал u(t), поступающий в непрерывную часть системы. При использовании АЦП и ЦАП, имеющих достаточно большое число разрядов, эффектами квантования по уровню часто пренебрегают. При этом структурную схему цифровой системы управления можно представить в виде, приведенном на рисунке 7.

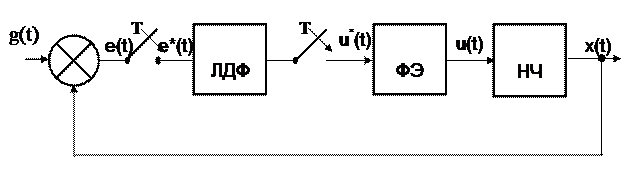
Рисунок 7 – Функциональная схема цифровой системы управления без учета квантования по уровню

1.2 Линейные разностные уравнения

Функцию е*(t) на выходе ИИЭ называют решетчатой функцией

.

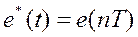При этом

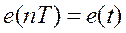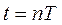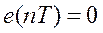при ;

при .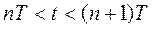

Линейные дискретные системы описываются линейными разностными уравнениями

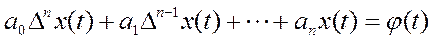, (4)

где x(t) – неизвестная дискретная функция, φ (t) – известная функция времени, определяемая входным воздействием, 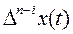(n=0,1,2,…) - конечные разности, характеризующие скорости изменения решетчатых функций. Конечные разности решетчатых функций являются дискретными аналогами производных непрерывных функций.

Конечная разность нулевого порядка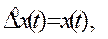

конечная разность первого порядка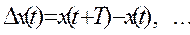

конечная разность n-ого порядка 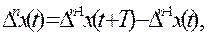Т – период квантования.

Уравнение (4) можно привести к виду [1]

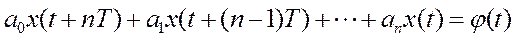. (5)

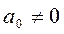Если и 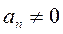уравнение (5) называют разностным уравнением n-го порядка.

Для решения разностных уравнений используются следующие методы: - классический состоит в нахождении общего и частного решений подобно тому, как это делается при решении линейных дифференциальных уравнений;

- рекуррентный, он используется при решении разностных уравнений с помощью цифрового компьютера;

- метод, основанный на использовании z-преобразования.

В последнем случае решение разностного уравнения находится как обратное z-преобразование от изображения X(z) сигнала 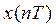, которое определяется по формуле

,

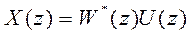где 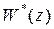- передаточная функция в 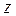-изображениях,

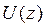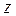- -изображение известного сигнала 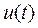. Из многих известных методов нахождения обратного z-преобразования часто используют метод разложения в степенной ряд и метод разложения на простые дроби. Примеры применения этих методов приведены в Приложении.

1.3 Определение z-преобразования

Z-преобразование числовой последовательности х(nΤ) определяется как степенной ряд вида z^-n с коэффициентами, равными значениям х(nΤ). Это преобразование имеет вид

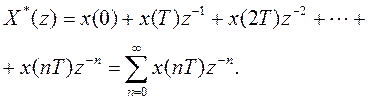
(6)

Преобразование (6) устанавливает соответствие между дискретной функцией 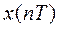, называемой оригиналом, и функцией комплексной переменной 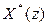, называемой изображением или z-изображением.

Прямое z-преобразование, т.е. нахождение z-изображения по оригиналу, условно записывается в виде

;

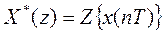обратное z-преобразование записывается в виде

.

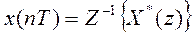Z-преобразование от наиболее распространенных функций и его свойства приведены в приложениях А и Б.

1.4 Связь z-преобразования и дискретного преобразования Лапласа

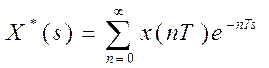Выражение

(7)

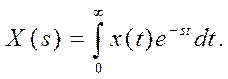является дискретным аналогом преобразования Лапласа непрерывной функции x(t) (L-преобразования):

Отличие заключается в том, что

• интеграл в L-преобразовании (прямом преобразовании Лапласа) заменяется суммой,

• непрерывная функции х(t) заменяется соответствующей решетчатой функцией х(nΤ) ,

Символическая форма записи прямого дискретного преобразования Лапласа (L_D-преобразования)

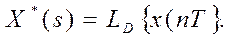Введем новую переменную z=е^sΤ . Тогда (7) можно записать так

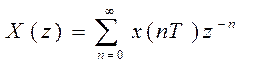. (8)

Таким образом, связь между z-преобразованием и дискретным преобразованием Лапласа можно записать в виде соотношения

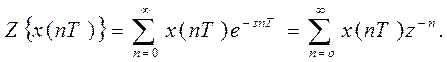(9)

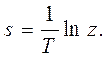Поскольку е^sΤ= z , 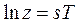, тогда

1,5 Представление данных в импульсной форме

Используя преобразование Лапласа, получим структурную схему импульсной системы, приведенной на рисунке 5.

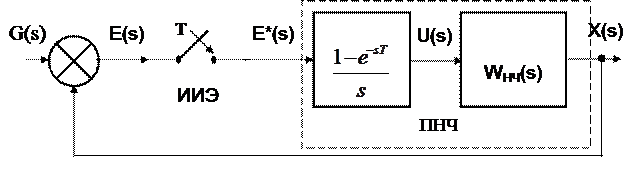
Рисунок 8 – Структурная схема импульсной системы

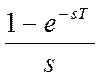Элемент, изображенный на рисунке 8 в виде ключа, соответствует идеальному импульсному элементу, а блок, содержащий передаточную функцию

соответствует фиксатору нулевого порядка.

Функция Е^*(s), называемая преобразованием со звездочкой, определяется выражением

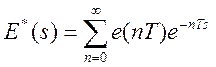. (10)

Следует отметить, что в реальной системе сигнала Е^*(s) не существует, он появляется лишь в результате математических операций.

Выражение (10) может быть представлено в другой форме

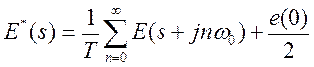, (11)

где 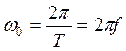- частота квантования в рад/с, 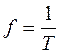- частота квантования в герцах.

Уравнение (11) устанавливает связь между изображениями Лапласа функции 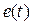и решетчатой функции 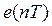, т.е. между обычным и дискретным преобразованием Лапласа при условии 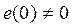. Если выполняется условие 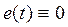при 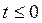, то используется уравнение

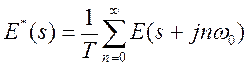(12)

Операцию нахождения 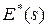по 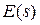, определяемую соотношениями (7) и (8), называют D-преобразованием и обозначают

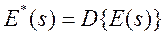. (13)

С помощью D-преобразования можно получить спектральные или частотные характеристики идеального импульсного элемента (квантователя). Заменив в (12) s на jω, находим связь между спектрами входного и выходного сигналов идеального импульсного элемента

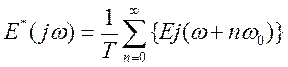. (14)

Уравнение (14) означает, что частотный спектр на выходе квантователя представляет собой сумму частотных спектров непрерывного сигнала на входе, смещенных по оси частот на величину nω₀.. Спектр 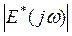полностью определяется диапазоном 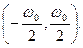или, в силу симметрии – диапазоном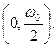

1.6 Импульсная передаточная функция

Введем понятие передаточной функции разомкнутой импульсной системы, структурную схему которой получим, разомкнув цепь обратной связи в системе (рисунок 8).

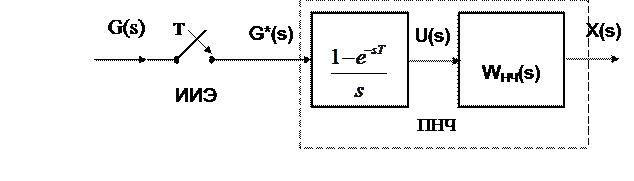
Рисунок 9 – Разомкнутая импульсная система

Передаточная функция непрерывной части и экстраполятора нулевого порядка (передаточная функция непрерывной приведенной части)

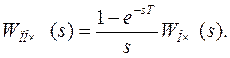(15)

В общем случае экстраполятор нулевого порядка не изображают отдельным блоком, и структурную схему разомкнутой системы представляют в виде (рисунок 10)

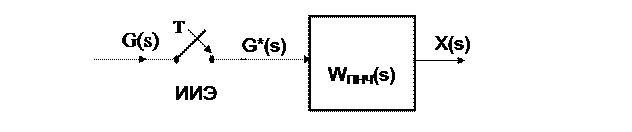
Рисунок 10 – Эквивалентная структурная схема разомкнутой импульсной системы

Выход ПНЧ импульсной системы представляет собой непрерывный сигнал, описываемый функцией времени х(t). Для упрощения анализа принято рассматривать этот сигнал в дискретные моменты времени, совпадающими с моментами замыкания ИИЭ на входе. Это равносильно включению фиктивного ИИЭ на выходе системы, работающего синхронно и синфазно с основным импульсным элементом и рассмотрению в качестве выходной переменной функции х*(t) (рисунок 11).

Рисунок 11 – К определению передаточной функции импульсной разомкнутой системы

Изображение по Лапласу сигнала на выходе х(t) определяется выражением

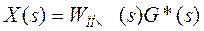. (16)

Используя D-преобразование, т.е. нахождение X*(s) по X(s) и полагая х(0)=0, получим

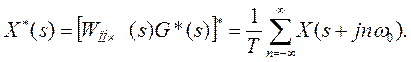(17)

Из (17) видно, что дискретный сигнал Х*(s) представляет бесконечную

последовательность входных сигналов. Тогда из (16) и (17) будем иметь

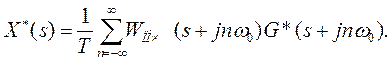(18)

Поскольку G*(s) является периодической функцией с периодом 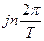, т.е. 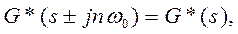то (18) приобретает вид

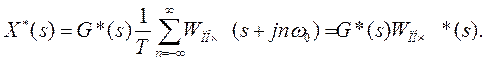(19)

Если в (19) заменить е^Тs=z, т.е. представить все функции в виде

z-преобразований, то получим

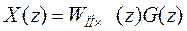. (20)

Теперь мы можем назвать 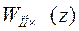импульсной передаточной функцией (ИПФ). Она связывает входной и выходной сигналы в моменты квантования и может быть определена как отношение z-изображения импульсного выхода системы к изображению импульсного входа системы при нулевых начальных условиях. Заметим, ИПФ не позволяет получить информацию о характере изменения х(t) в промежутках между моментами квантования. Этой информации не содержит ни (20), ни (19).

Для определения ИПФ можно воспользоваться другим путем.

L-преобразование выхода импульсной системы

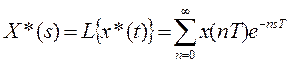. (21)

Значения 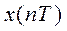сигнала на выходе ПНЧ для t=nТ определяются из выражения для функции х(t), имеющего вид:

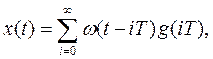
где ω(t) – импульсная переходная (весовая) функция ПНЧ с передаточной функцией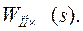

(Это выражение получается на основании теоремы о свертке (умножение изображений). Если х₁(t) и х₂ (t) являются оригиналами, а Х₁(s) и Х₂(s) их изображения, то 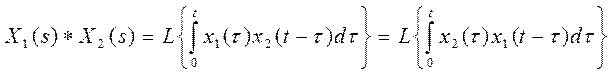. Интеграл в правой части называют сверткой функций х₁(t) и х₂ (t). Его обозначают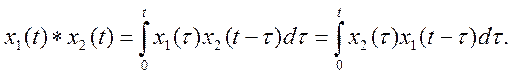

Поэтому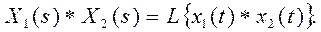

.

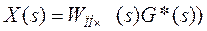Следовательно, значения выхода в моменты времени t=nТ равны

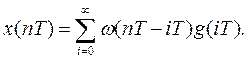(22)

Подставляя (22) в (21), получим

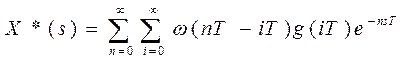. (23)

Подстановкой m=n-i и n=i+m уравнение (23) приводится к виду

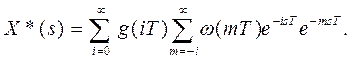
Учитывая, что ω(mТ)≡0 для m <0, окончательно получим

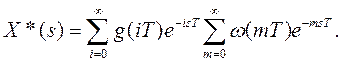(24)

Исходя из определения L_D-преобразования, можно привести уравнение (24) к виду

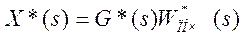, (25)

где

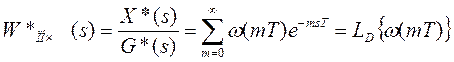(26)

- ИПФ разомкнутой системы в s-форме (так называемая импульсная передаточная функция со звездочкой).

Таким образом, ИПФ в s-форме является отношением дискретных преобразований Лапласа выхода и входа при нулевых начальных условиях.

Путем подстановки е^Тs=z в(24) и (25) можно получить уравнения для

z-изображений

,

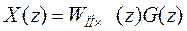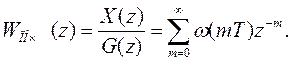(27)

Здесь 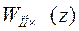- импульсная передаточная функция в z-форме.

Выражение (27) показывает, что ИПФ представляет z-преобразование импульсной переходной функции ПНЧ системы, т.е.

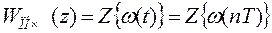(28)

или

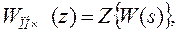(29)

в предположении, что z-преобразованию подвергается импульсная переходная функция 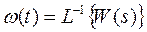или соответствующая ей решетчатая функция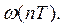

Рассмотрим определение импульсной передаточной функции системы (рисунок 11) с формирующим элементом типа фиксатора нулевого порядка. В соответствии с выражением (29) запишем ИПФ в виде

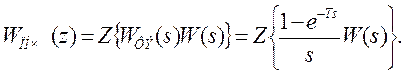
Сделав замену 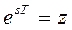и обозначив ,

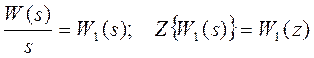имеем

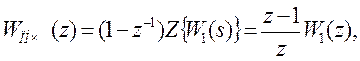
где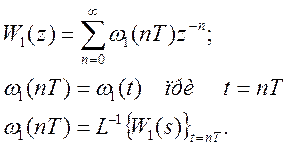

Примеры определения ИПФ по приведенному выше методу приведены в приложении В.

В общем виде ИПФ можно представить так:

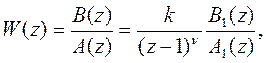
где А(z), В(z) – полиномы степеней n и m, соответственно, причем m≤ n; k – коэффициент передачи системы; А₁(z), В₁(z) – нормированные полиномы степеней n-ν и m, такие, что В₁(0)/ А₁(0)=1.

Импульсную передаточную функцию можно характеризовать следующими числовыми показателями:

- порядком системы n, который определяется числом полюсов или степенью знаменателя ИПФ W(z);

- порядком астатизма ν – числом полюсов W(z), равных 1;

- числом нулей (степенью полинома числителя) ИПФ.

Свойства ИПФ, которые могут быть полезны при анализе и синтезы импульсных систем:

- импульсная передаточная функция в s-форме

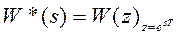
является периодической функцией с периодом jω₀,

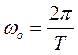- частота квантования;

- значения ИПФ W(z) всегда действительны при z=1 (ω=0) и z=-1 ( 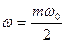), конечны при z=1, если 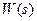не имеет полюсов в начале координат (корней знаменателя 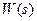, равных нулю);

- полюсы z импульсной передаточной функции W(z) связаны с полюсами s передаточной функции 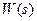приведенной непрерывной части импульсной системы соотношением 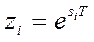. Число полюсов W(z) равно числу полюсов 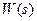, т.е. степень знаменателя W(z) равна степени знаменателя .

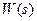1.4 Частотные характеристики импульсных систем

Физический смысл характеристик импульсных и непрерывных систем очень близок. Особенностью этих характеристик для импульсных систем является то, что они устанавливают связь между гармоническими последовательностями (гармоническими решетчатыми функциями) на входе и выходе импульсного фильтра с передаточной функцией 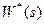или W(z). Огибающие решетчатых функций изменяются по гармоническому закону.

Если на вход линейного импульсного фильтра подается гармоническая последовательность 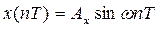, то после окончания переходного процесса на выходе получим также гармоническую последовательность .

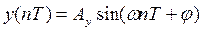Заметим, что в отличие от непрерывной гармонической функции гармоническая решетчатая в общем случае не является периодической . Кроме того, амплитуды А_х и А_у не обязательно являются теми максимальными значениями, которых могут достигать те или иные члены соответствующих последовательносте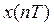й и 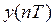. Амплитуды всегда будут определять лишь верхние границы, но не обязательно максимумы членов этих последовательностей.

Если исходная информация о системе представлена передаточными функциями 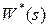или W(z), то для перехода к частотным характеристикам используется замена 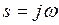или 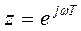. В результате такой замены аргумента получаем комплексный коэффициент передачи импульсной системы .

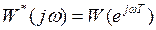В общем случае импульсная передаточная функция

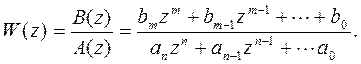(30)

Сделав замену 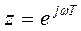, получим

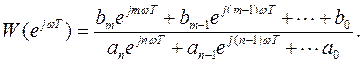(31)

Комплексный коэффициент передачи

,

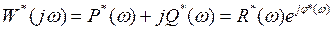где 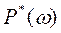- вещественная часть,

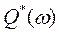- мнимая часть,

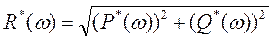- амплитудная частотная характеристика,

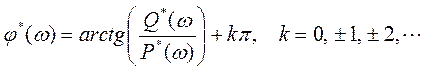- фазовая частотная характеристика,

,

.

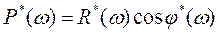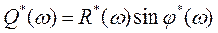При фиксированном значении ω комплексный коэффициент передачи изображается вектором на плоскости 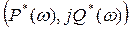. При изменении частоты ω конец вектора 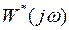описывает некоторую кривую, которую называют годографом комплексного коэффициента передачи системы или её АФЧХ.

Отметим основные свойства частотной характеристики импульсной системы, которые вытекают из свойств импульсной передаточной функции:

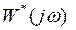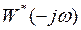- частотные характеристики ИС являются периодическими функциями относительно частоты ω с периодом повторения ω₀=2π/Т. Это значит, что при построении этих характеристик достаточно ограничится изменением ω в диапазоне 2π/Т, например, от (–π/Т) до (+π/Т). Если учесть, что участки частотной характеристики в диапазоне (–π/Т) до (+π/Т) симметричны (поскольку и - комплексные сопряженные функции), то можно ограничиться построением частотной характеристики в интервале частот от 0 до π/Т.

- АФЧХ импульсной системы заканчивается на вещественной оси, так как для ω=π/Т комплексный коэффициент передачи всегда действительное число.

Свойство периодичности частотной характеристики импульсной системы физически объясняется стробоскопическим эффектом, который проявляется в том, что гармоническая решетчатая функция 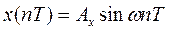на входе импульсного фильтра не изменяется при изменении частоты огибающей на любую величину, кратную ω₀, т.е. последовательность 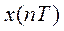будет одной и той же при всех частотах огибающей, равных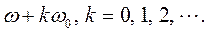

АФЧХ ИС можно построить как по выражению 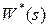или W(z), так и по передаточной функции приведенной непрерывной части с использованием выражений

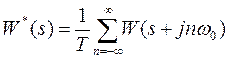
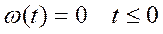; (32)

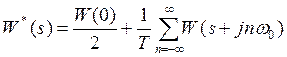
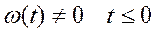(33)

при 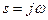или её импульсной переходной функции на основе выражения

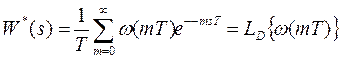при 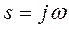. (34)

Примеры построения АФЧХ импульсной системы приведены в приложении Д.

1.5 Логарифмические частотные характеристики импульсных систем

Изображение частотных характеристик в виде ЛЧХ удобно тем, что возможно рассмотрение частотных свойств в большом диапазоне амплитуд и частот их можно аппроксимировать прямолинейными отрезками.

Многие методы анализа и синтеза импульсных систем (например, критерий Рауса-Гурвица и логарифмический критерий) основаны на том, что границей устойчивости на плоскости корней характеристического уравнения (s-плоскости) является мнимая ось.

На рисунке 8 приведена s-плоскость, соответствующая характеристическому уравнению 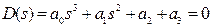. Корни характеристического уравнения в общем случае .

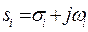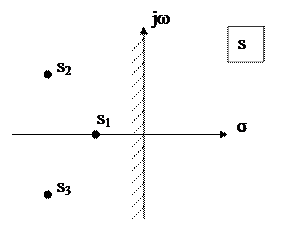
Рисунок 8 – s-плоскость корней характеристического

уравнения устойчивой системы третьего порядка.

Границей устойчивости является мнимая ось. Границей устойчивости на z-плоскости является окружность единичного радиуса. Поясним это утверждение. Связь z и s выражается формулой 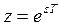. Тогда граница устойчивости на z-плоскости описывается выражением 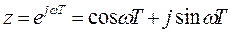, что соответствует окружности единичного радиуса на комплексной плоскости (рисунок 9).

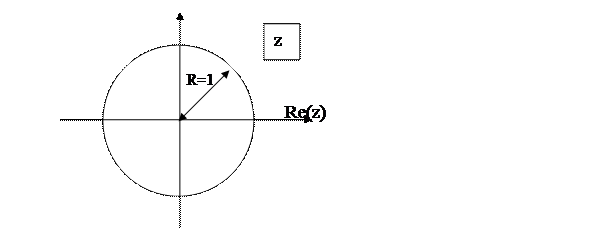
Рисунок 9 – Окружность единичного радиуса, отображающая мнимую ось s-плоскости на z-плоскости

Это обстоятельство препятствует применению методов анализа и синтеза непрерывных систем на основе ЛЧХ для импульсных систем. Применение ЛЧХ для расчета импульсных систем основано на билинейом преобразовании, которое выражается соотношением

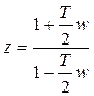(35) или 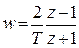, (36) т.е. на переходе от z-преобразования к

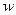-преобразованию. С помощью этого преобразования единичная окружность z-плоскости отображается на мнимую ось 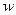-плоскости. Докажем зто. Переменная 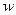называется частотой на 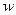- плоскости (псевдочастотой).

Найдем связь между частотой ω на s-плоскости и псевдочастотой w.

Для этого сделаем подстановку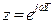

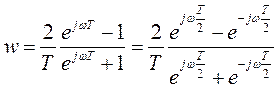. (37)

Выражение (37) путем применения формулы Эйлера можно привести к виду

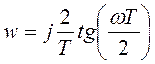. (38)

При ω=0 w=j0, а при ω→ ω₀ /2 ωТ/2→π/2 и w → j∞ .Следовательно, отрезок 0≤ jω<jω₀/2 на s-плоскости отображается в верхнюю половину единичной окружности на z-плоскости и в верхнюю половину мнимой оси на w-плоскости. На рисунке 10 приведены отображения основной полосы s-плоскости (-jω₀/2≤ jω≤jω₀/2) на z-плоскость и w-плоскость, откуда видно, что областью устойчивости на w-плоскости является ее левая половина.

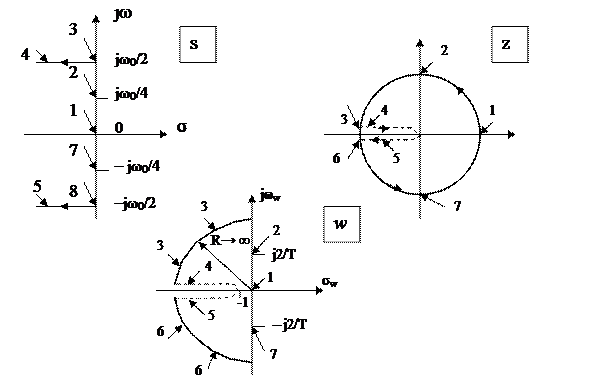
Рисунок 10 – Отображение s-плоскости на z-плоскость и w-плоскость

Пусть 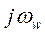есть мнимая часть переменной w. Мы будем называть ω_w частотой на w-плоскости (псевдочастотой). Тогда (38) можно представить в виде:

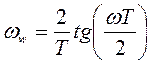. (39)

Это выражение устанавливает связь между частотой на s-плоскости и частотой на w-плоскости. Билинейное преобразование можно использовать для построения диаграммы Найквиста. Поскольку область устойчивости на s-плоскости и w-плоскости совпадают, контур Найквиста на w-плоскости имеет тот же вид, что и на s-плоскости. Следовательно, можно воспользоваться методами построения диаграммы Найквиста для непрерывных систем.

Билинейное преобразование позволяет распространить методику построения логарифмических частотных характеристик непрерывных систем на импульсные системы. Для перехода от импульсной передаточной функции W(z) к характеристике W(w) следует сделать подстановку

.

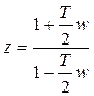Чтобы перейти к частотной передаточной функции W(jω_w) необходимо заменить w на jω_w. Далее, используя методику построения логарифмических частотных характеристик, строим ЛАЧХ. По оси ординат откладываем L(ω_w)=20lg|W(ω_w)| по оси абсцисс частоту ω_w в логарифмическом масштабе. Примеры построения логарифмических частотных характеристик импульсной системы приведены в приложении Е.

Контрольные задания

2.1 Общие положения

Учебным планом по дисциплине «Импульсные и цифровые системы управления» предусмотрено выполнение контрольной работы. В качестве промежуточной аттестации предусмотрен зачет, Выполнение контрольной работы имеет целью практическое освоение методов математического описания и построения временных и частотных характеристик импульсных систем управления. Для успешного выполнения контрольной работы необходимы знания теории линейных непрерывных систем автоматического управления и освоение соответствующих разделов теории линейных дискретных (импульсных и цифровых) систем управления.

Контрольная работа включает четыре задания, каждое из которых имеет двадцать вариантов. Вариант задания выдает преподаватель во время установочной сессии.

Контрольная работа выполняется на одной стороне белой нелинованной бумаги формата А4 по ГОСТ 2.301 в соответствии с ГОСТ Требования к оформлению текстовых документов. Рекомендуется оформлять контрольную работу с помощью ЭВМ. Допускается и рукописный способ с соблюдением всех требований к оформлению. Образец титульного листа приведен в приложении Ж.

Каждое задание контрольной работы оформляется в следующем порядке: вариант задания, условие задачи, исходные данные в соответствии с заданным вариантом, решение задачи с необходимыми пояснениями, результаты расчетов в виде таблиц и графиков, анализ полученных результатов и выводы. Вывод формул выполнять в общем виде. Численные значения параметров подставлять в окончательные формулы. При использовании для построения характеристик программ Matlab или других специализированных программ необходимо сначала получить расчетные формулы.

Иллюстрации (схемы, графики и пр.) именуют рисунками и помещают в разрыв текста после первой ссылки на них. Иллюстрации рекомендуется выполнять с помощью ЭВМ. Допускается выполнять простым карандашом или черной пастой с применением чертежных инструментов.

Контрольная работа должна быть выполнена до начала сессии и представлена для проверки преподавателю. Правильно выполненная контрольная работа должна быть защищена. Примерные контрольные вопросы приведены в приложении И. Без успешной защиты контрольной работы студент не допускается к зачету.

2.2 Задача 1. Определить импульсную передаточную функцию 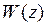, для импульсной системы, приведенной на рисунке 2.1, непрерывная часть которой имеет передаточную функцию 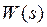, а формирующий элемент является экстраполятором нулевого порядка.

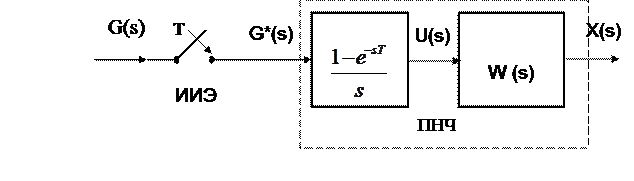
Рисунок 2.1 – Разомкнутая импульсная система

Таблица 1 – Варианты задачи 1

Вариант		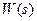К	τ, с	Период квантования Т, с
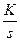				0,1
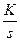				0.02
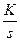		0,5		0,2
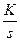				0,1
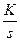				0.5
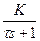		1,5	0,1	0,01
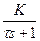				0,1
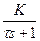			0,5	0,02
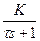			0,4	0,05
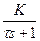		0,5		0,15
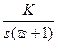		0,2	0,1	0,02
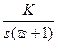				0,1
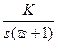				0,03
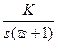			0,8	0,1
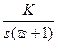				0,05
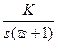			0,5	0,01
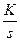				0.01
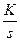				0,5
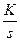				0,2
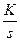				0,1

Методические указания. Для выполнения задачи необходимо изучить теоретический материал по литературным источникам [1стр.195-207, 2 стр. 212-242]. Необходимо уяснить сущность дискретного преобразования Лапласа, z-преобразования, понятие импульсной передаточной функции, рассмотреть методику ее определения, разобрать примеры определения импульсной передаточной функции, приведенные в приложении В и в сборнике задач [3 стр.103-112].

2.3 Задача 2. На рисунке 2.1 изображена структурная схема импульсной системы. Передаточная функция непрерывной части 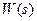. Т- период квантования, 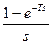- передаточная функция формирующего элемента.

Требуется:

1 Определить переходные функции системы для периода квантования Т с и для периода квантования Т₁=0,1Т с, а также для непрерывной системы, в которой отсутствует импульсная часть.

2 Построить переходные характеристики для условий п.1 .

3 Сделать выводы.

Таблица 2 – Варианты задания 2

Вариант	Передаточная функция непрерывной части	Период квантования Т	Постоянная времени τ	Коэффициент усиления К
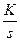		0.5
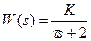		0,1	0,1
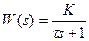		0,4	0,2
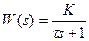		0,1	0,4
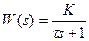		0,2	0,5
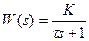		0,2	0,1
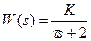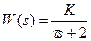			1,5
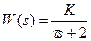			2,0
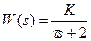			1,5

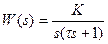Продолжение таблицы 2

Вариант	Передаточная функция непрерывной части	Период квантования Т	Постоянная времени τ	Коэффициент усиления К
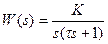				0,5
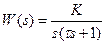		1,5
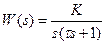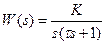			0,8
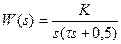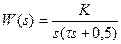		0,2	2,5
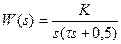			0,5
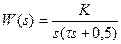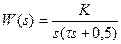			1,5

Примеры выполнения задания 2 приведены в приложении Г.

2.4 Задача 3. Для системы, изображенной на рисунке 2.1 построить диаграммы Найквиста при следующих условиях:

1) период квантования Т с,

2) период квантования 0,1Т с,

3) квантователь и экстраполятор, образующие импульсную часть, удалены из системы, т.е. она будет непрерывной. Варианты задания приведены

4) варианты задания приведены в таблице 1.

Методические указания.

Примеры построения диаграммы Найквиста (АФЧХ) импульсной системы приведены в приложении Д.

2.5 Задача 4. Для системы, изображенной на рисунке 1.1 построить логарифмические частотные характеристики при следующих условиях:

1) период квантования Т с,

2) период квантования 0,1Т с,

3) квантователь и экстраполятор, образующие импульсную часть, удалены из системы, т.е. она будет непрерывной.

4) варианты задания приведены в таблице 2.

Примеры построения логарифмических частотных характеристик приведены в приложении Е

Приложение А – Преобразование Лапласа и z-преобразование некоторых функций x(t)

Таблица А1

x(t)	x(kT)	X(s)	X(z)
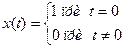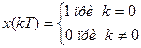		_	1
		_
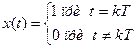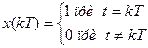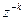1(t)	1(kT)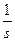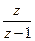
t	kT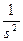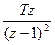

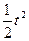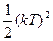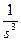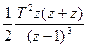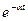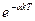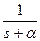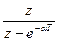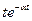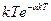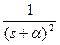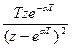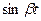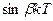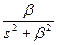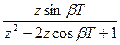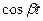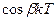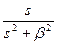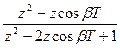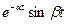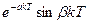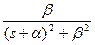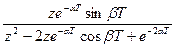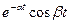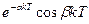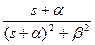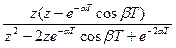Приложение В – Основные свойства и теоремы

Z-преобразования

Линейность. Если функции x₁(kT), x₂(kT) и x(kT) преобразуемы по z и имеют z-преобразования, соответственно равные Х₁(z), Х₂(z), Х (z), и - постоянный коэффициент, то

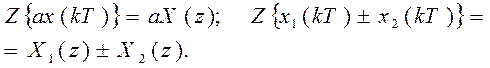
Сдвиг во временной области. Если функция x(kT) преобразуема по z и имеет z-преобразование Х (z), то при сдвиге решетчатой функции вправо (запаздывание) имеем

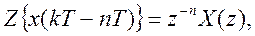где n- неотрицательное целое число; х(kT)=0 при k<0.

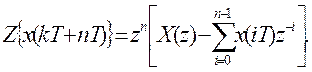При сдвиге влево (опережение)

Если x(kT)=0 при k=0,1,…n-1, то последнее выражение упрощается

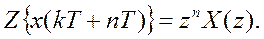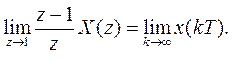Конечное значение.Если функция x(kT) преобразуема по z и имеет z-преобразование Х (z), которое не имеет полюсов |z| то

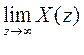Начальное значение. Если функция x(nT) имеет z-преобразование Х (z) ипредел существует, то

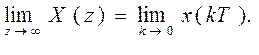Изменение масштаба в области z. Если функция x(kT) преобразуема по z и имеет z-преобразование Х (z) иα- целое число, то
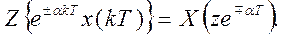