Пример. Для газа в сосуде концентрация частиц около точки r есть число частиц в единице объема около r

,

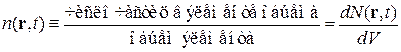изменяется с течением времени хаотически.

Событие – наблюдение определенной концентрации .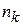

Проводим N измерений концентрации, результат 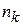наблюдается 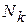раз, тогда вероятность результата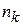

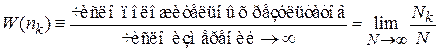, (1.1)

.

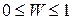Зависимость 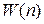называется функцией распределения вероятности событий.

Несовместимые события А₁, А₂,…, А_k не могут произойти одновременно. Например, если бросать шестигранную кость, на каждой грани которой написано число от 1 до 6, можно получить результат: или 1, или 2,…, или 6. Выполняется теорема сложения вероятностей несовместимых событий – вероятность сложного события A или B равна сумме вероятностей отдельных событий. Действительно, выполняется

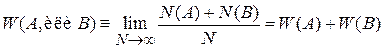. (1.2)

Если (А₁, А₂,…, А_k) – полный набор несовместимых событий, то какое-либо одно из них обязательно происходит, тогда выполняется

.

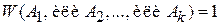С учетом (1.2) получаем условие нормировки вероятностей для полного набора несовместимых событий

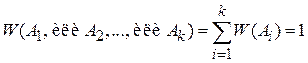. (1.3)

Пример. Движения молекулы газа по и против некоторой оси образуют полный набор независимых направлений движения

W(влево) + W(вправо) = 1.

Если у гамильтониана системы все направления равноправные, тогда

W(влево) = W(вправо) = 1/2.

Независимые события А1, А2,…, Аk не влияют друг на друга. Например, частицы идеального газа движутся независимо друг от друга, и положение одной частицы не влияет на положение другой частицы. Выполняется теорема об умножении вероятностей независимых событий – вероятность сложного события А и B равна произведению вероятностей отдельных событий

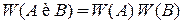, (1.4)

Для k независимых событий

.

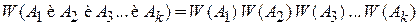Пример. В объеме V₀, все точки которого равноправные, находится частица. Объем V₀ разбиваем на N одинаковых ячеек объемом 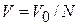. При обследовании всех ячеек, т.е. при 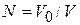измерениях, положительный результат будет только в одной ячейке. Вероятность найти частицу в одной произвольной ячейке согласно (1.1)

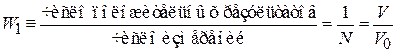. (1.4а)

Если в V₀ находится m независимых частиц, то вероятность, что весь газ окажется в объеме V, согласно теореме (1.4) равен

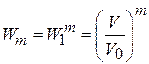. (1.4б)

Характеристики случайной дискретной величины

Среднее значение величины

Пусть для x возможные значения: x₁, x₂, …, x_k.

Измерения проводятся N раз, результат x_i наблюдается N_i раз, тогда

.

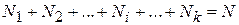Среднее значение

.

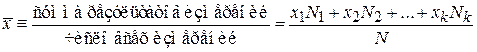При 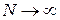согласно (1.1)

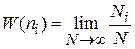
получаем

.

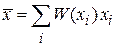Аналогично

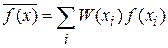. (1.5)

Среднее значение величины равно сумме произведений ее значений на вероятности этих значений.

При 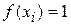получаем 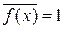и (1.5) дает нормировку вероятностей

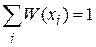. (1.6)

Свойства среднего

Для 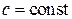и независимых случайных величин x и y выполняются теоремы:

1.

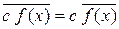
– постоянная выносится из под знака усреднения;

2.

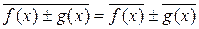
– среднее от суммы равно сумме средних,

3.

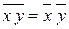
– среднее от произведения независимых величин равно произведению их средних.

Доказательство свойства 2

Используем определение среднего (1.5)

.

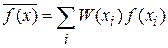Функция 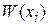описывает распределение случайной величины x и она одинакова для 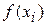и 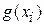, тогда

;

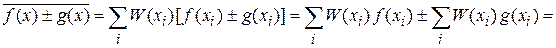
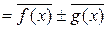Доказательство свойства 3

Используем определение среднего и функцию распределения 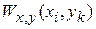для независимых случайных величин x и y. Согласно теореме об умножении вероятностей независимых событий

.

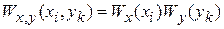Тогда получаем

.

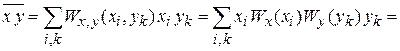
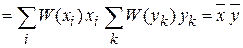ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ

Отклонение от среднего

.

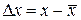Среднее отклонение от среднего любой величины равно нулю

.
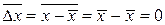