Математичний вираз другого закону ТТД

Для оборотного циклу Карно маємо: 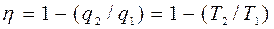;звідки: 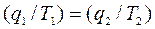, або

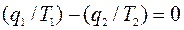
Враховуючи, що теплота q1 позитивна, а теплота q2 негативна, запишемо:

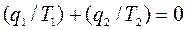або 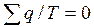, (6.1)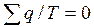

Це можна припустити, якщо під q₂ розуміти не абсолютну кількість теплоти,яку віддає робоче тіло холодильнику з температурою Т₂, а його значення в алгебрі, яке за списком негативне.

Відношення q/T називається зведеною теплотою. З рівняння (6.1) виходить, що в оборотному циклі Карноалгебраїчна сума зведеної теплоти дорівнює нулю.

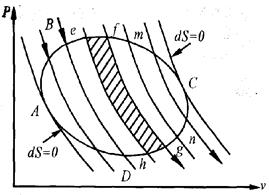Неважко показати, що рівність (6.1) справедлива не тільки для циклу Карно, але і для будь-якого оборотного циклу. З цією метою розглянемо в p, v - діаграмі довільний оборотний цикл (мал. 6.1).

Проведемо велику кількість близько розташованих адіабат, які розіб'ють довільний цикл на нескінченно велику кількість елементарних циклів e-f-g-h, f-m-n-g і т.д. Кожен такий елементарний цикл складається з двох адіабат і двох елементарних відрізків контура даного циклу. Зважаючи на нескінченно малі довжини цих відрізків,зміни температури по ним

Мал. 6.1 так само нескінченно малі.

Отже, в межі ці відрізки можна вважати ізотермами, а цикли елементарними циклами Карно. Сукупна дія елементарних циклів однакова з дією кругового циклу ABCD.

Робота розширення по адіабаті f-g циклу e-f-g-h дорівнює роботі стиснення по адіабаті g-f циклу f-m-n-g. Таким чином, адіабатні процеси кінець кінцем не впливають на величину роботи, теплота ж під час цих процесів не підводиться і не відводиться. Сумарна дія елементарних циклів зводиться до сукупної дії елементарних процесів e-f, f-n, n-g, g-h і т. д., тобто однаково з дією кругового процесу по контуру ABCD.

Для кожного елементарного циклу Карно справедливе співвідношення (6.1). Підсумовуючи ці співвідношення для всіх елементарних циклів, для даного довільного циклу одержимо: 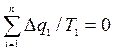, (6.2)

У межі для нескінченно великого числа цих елементарних циклів, тобто для циклу ABCD

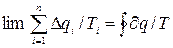
Розрахуючи (6.2), маємо: 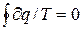, (6.3)

Відомо, якщо інтеграл по замкнутому контуру дорівнює нулю, то підінтегральний вираз є повним диференціалом деякої функції стану S, називається ентропією, тобто:

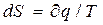або 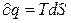, (6.4)

цей вираз одержаний Клазіусом в 1834г, є математичним виразом другого закону термодинаміки для оборотного циклу і називається першим інтегралом Клазіуса.

Необоротні цикли.

Термічний ККД необоротного циклу менше, ніж термічний ККД циклу Карно, тобто:

ηtннеоб<ηооб. Звідки 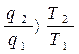, або 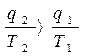, (6.5)

Враховуючи, що теплота q₂ - величина негативна (алгебраічне значення теплоти q₂, що відводиться, за змістом негативне), нерівність (6.5) можна представити у вигляді:

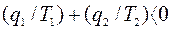, або 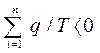, (6.6)

Ця нерівність показує, що алгебраїчна сума приведених теплот для необоротного циклу Карно менше нуля, тобто є величиною негативною.

Для довільного необоротного циклу, складеного з нескінченно великої кількості необоротних елементарних циклів, маємо :

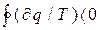, (6.7)

Ця нерівність є математичним виразом II-го закону ТТД для довільного необоротного циклу і називається другим інтегралом Клазіуса. Узагальнюючи приведені міркування для оборотних і необоротних кругових процесів, можна написати:

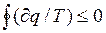, (6.8)

де знак рівності відноситься до оборотних циклів, і є аналітичним виразом П-го закону ТТД.

Рівняння (6.8) показує, що приріст ентропії змінюється оберненопропорційно до температури. Отже, ентропія побічно через температуру, характеризує кількість теплоти, яка може бути перетворена в роботу, тобто її поняття тісно переплітається з суттю II-го закону ТТД, що встановлює умови, при яких в теплових двигунах можливий перехід теплоти в роботу.