Studying laws of a direct current
A purposeof the work is to measure resistance of a conductor by different methods, to calculate the specific resistance, to examine relation Rp= f(1).
Instrumentation and appliances: an experimental plant.
Theoretical part
1. The ordered motion of electric charges is called the electric current. An electric current in metals is the motion of the conductivity electrons. In conducting solutions (electrolytes) ions are the mobile charges. The ions and the electrons carry charges in gases.
Intensity and density are the quantative characteristics of the electrical current. Intensity of current is the charge dq passesthrough a cross section of a conductor in a time dt:
.
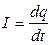If the same amount of electric charges flows through any section of conductor at the equal period of time, the current intensity is constant value I= dq/dt = const. If the current changes by time, it is alternating current dq/dt≠const. The intensity of current is a scalar value and measured in amperes in the SI system. Current intensity is measured in milliamperes (mA) and microamperes (μA) too.
If current is assigned irregularly along the surface S, then the current density j is defined in every point of the surface. The current density is the ratio
,
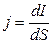where dS is an area perpendicular to the current direction dI which goes through this area.
The current intensity I through the given surface S can be found with the help of integration:
.
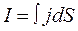If the current I is assigned regularly through the given surface S then the current density-j=I/S=const. The current density is a vector value and inSI system measured in amperes divided by square meter(A/m2).
The density of a charge j can be assigned by concentration of the charges, it’s value and velocity
.
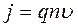2. There is relationship between the voltage U applied to the ends of the conductor and the current in it for each conductor if the condition of the conductor is invariable:
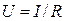.(8.1)
It’s the Ohm’s law for the part of the electric circuit in integral form. According to the Ohm’s law in the differential form j=σE the current density j in the conductor is directly proportionate to the electric intensity E in it, where σ is specific electroconductivity of the conductor. The Ohm’s law for the closed circuit is
,
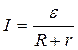where ε - electromotive force,
R - external resistance of the conductor,
r - internal resistance of current source.
When the current passes through the conductor, the latter is being heated. The quantity of the produced heat in the conductor is proportionate to its resistance, square value of current intensity and time:
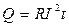. (8.2)
If the current intensity changes in time, then:
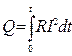. (8.3)
The formulas (8.2) and (8.3) represent the Joule-Lenz’ law. The heat quantity Q, which turns from the volume unit into the time unit of the conductor, is called the power of the current. The Joule-Lenz’ law in differential form is:
.
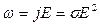3. Simple electric circuits are closed loops. The calculation of the ramified electric circuit is more complex but significantly simplified if we use Kirchhoff’s laws.
The first law deals with the junction points and states: the algebraic sum of the currents at any junction point equals to zero (Fig. 8.1). For the junction point A:
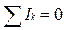
or -I1-I2+I3=0.
The second law deals with electric circuits: for any closed loop the algebraic sum of all incidences of voltage IiRi is equal to the algebraic sum of all the electromotive forces εi in this circuit.
For the 1 circuit
.
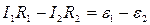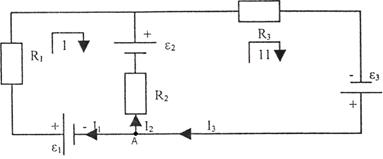
Figure 8.1
For the 2 circuit
.
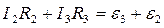4. The conductor’s resistance is directly proportional to its length and inversely proportional to its cross-section area
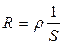, (8.4)
where ρ- the specific resistance of the conductor,
l - the length of the conductor,
S - cross-section area.
The conductors in the electric field can be connected in series and parallel.
When the conductors connected in series the current has the same value of I (fig. 8.2).
Voltage drop in each resistance
; 
; 
.
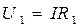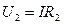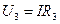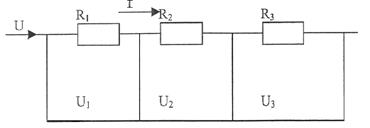
Figure 8.2
Adding right and left parts of these equations we obtain:
.
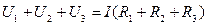Hence it follows, that for any n amount of resistances connected in series there is a common resistance:
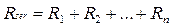.(8.5)
In case of parallel resistance the common current I is branched into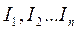 
currents.
Let us consider parallel connection for three conductors (fig. 8.3):
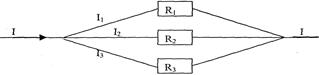
Figure 8.3
Voltage drop in each resistance is the same:
;
; 
; 
; 
; 
.
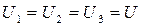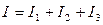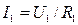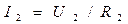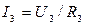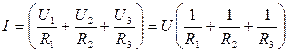In general for n amount of the conductors connected in parallel the total resistance may be expressed by the formula
.
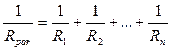Experimental part
An experimental device to measure the resistance consists of the column with wire and measuring block (fig.8.4).
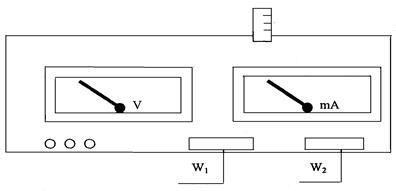
Figure 8.4
On the column there are two motionless brackets and a traveling one which can move along the column and be fixed in any position. The mark which is drawn between the upper and the lower brackets facilitates to define the length of the segment of resisting wire being measured.
The measuring part is placed in the separate block which has milliamperemeter, voltmeter and operating keys. Milliamperemeter is plugged in the resisting wire circle and used to measure the current and voltmeter to measure the voltage in the measured length of resisting wire. The switch W1 is used to choose the type of work and the switch W2 to choose the accuracy of current and voltage measurement.
1. Move the traveling bracket for 0,7 - 0,8 of length of the resisting wire, take it from the basis.
2. Press button W1 “МЕРЕЖА”.
3. Press button W3“МІСТОК”.
4. When pressing button W2 the scheme works in the Fig. 8.5.
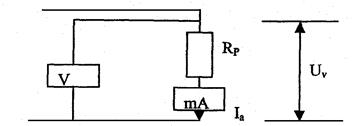
Figure 8.5
5. Write down the measurements which shows millliamperemeter and voltmeter and calculate R using the formula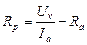 
, Ra= 0,15 Om, Ra = 2500 Om.
6. When pressing button W2, the scheme in the Fig. 8.6 works.
7. Make measurements of the millliamperemeter and voltmeter readings and calculate R using the formula:
, 
.
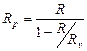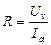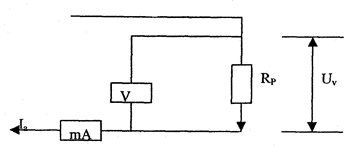
Figure 8.6
8. Measure with micrometer the diameter of the wire d, the length of the wire from the basis to the traveling contact l, calculate the specific resistance r using the formula
.
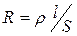9. Using one of the schemes of connection build up the constant value of the current I with the help of regulator. Moving the traveling contact of the resisting wire for a few marks find 8-10 values of the U.
10. Count 8-10 values of R using the formula which correspond to the switching on scheme.
11. Fill in the table with data:
| № | |||||||||
| Ia, A | |||||||||
| I, m | |||||||||
| Uv,V | |||||||||
| Rp, Om |
12. Build up the graph Rp =f(I).
13. Count the error for Rp . Make a conclusion about the work done.
Control questions
1. What is an electric current? Write the formula for the direct current.
2. Write the definition and formula for the alternating current.
3. Write the definition and formula for the current density.
4. Write the relationship between the current intensity and its density.
5. Write the Ohm’s law in integral form.
6. Write the relationship between the conductor resistance and conductor electroconductivity.
7. Write the Ohm’s law for the closed circuit.
8. Formulate and write the Joule Lenz’ law.
9. Formulate and write the first and the second Kirchhoff’s laws.
10. Write the dependence of the conductor resistance on its cross-section.
11. Deduce the formula for counting two resistors connected in series and parallel.
This instruction is worked out by S. Lushchin, reader of the physics chair.
Reviewer: S. Loskutov, professor of the physics chair.
ЛАБОРАТОРНА РОБОТА № 22.2
ВИМІРЮВАННЯ ЕЛЕКТРИЧНИХ ОПОРІВ
МЕТОДОМ МІСТКА УІТСТОНА
Мета роботи:визначити невідомі опори методом містка Уітстона.
Прилади і обладнання: реохорд, магазин опорів, два невідомих опора, нуль-гальванометр, акумулятор, ключ.
Теоретична частина
Електричним струмом називається будь-який впорядкований (спрямований) рух електричних зарядів. У провіднику під дією прикладеного електричного поля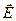 
вільні електричні заряди переміщуються: позитивні по полю, негативні – проти поля, тобто в провіднику виникає електричний струм, який називається струмом провідності. Для виникнення і існування електричного струму необхідно: 1) наявність вільних носіїв струму – заряджених частинок, здатних переміщуватися впорядковано; 2) наявність електричного поля, енергія якого, поповнюючись, витрачається на впорядкований рух.
Узагальнений закон Ома для неоднорідної ділянки кола представляється виразом
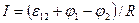, (9.1)
де I – струм на ділянці кола 1-2, ε12 – ЕРС, що діє на цій ділянці, φ1-φ2 – різниця потенціалів кінців ділянки, R – опір ділянки кола. Якщо на даній ділянці кола джерело струму відсутнє (ε12 = 0), то приходимо до закону Ома для однорідної ділянки кола:
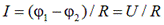(9.2)
Якщо коло замкнене, тобто точки 1 і 2 співпадають (φ1=φ2), отримуємо закон Ома для замкненого кола:
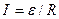, (9.3)
де ε – ЕРС, що діє в колі, R – сумарний опір всього кола. R = r + R1, r – внутрішній опір джерела струму, R1 – опір зовнішнього кола.
Для розрахунку розгалуженого кола, що містить декілька замкнених контурів (контури можуть мати спільні ділянки, кожен з них може мати кілька джерел струму і т. д.) використовують правила Кирхгофа.
Будь-яка точка розгалуження кола, в якій сходиться не менше трьох провідників із струмом, називається вузлом. Струм, що входить у вузол, вважається позитивним, а струм, який виходить з вузла, – негативним. Перше правило Кирхгофа: алгебраїчна сума струмів, що сходяться у вузлі, дорівнює нулю:
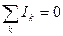. (9.4)
Друге правило Кирхгофа: у будь-якому замкненому контурі, вибраному в розгалуженому електричному колі, алгебраїчна сума добутків сили струму Ik і опору Rk , що відповідають ділянці контуру між двома вузлами, дорівнює алгебраїчній сумі ЕРС εk , що діють в цьому контурі:
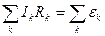. (9.5)
Для визначення опорів в роботі використовують місток Уітстона (рис. 9.1), де Rx – невідомий опір, R – магазин опорів, ADB – рео-
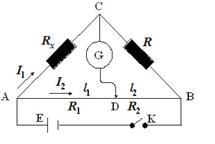
хорд.
Рисунок 9.1
Містком є галузь СD, що містить гальванометр G. Якщо замкнути ключ К, струм від джерела Е буде йти по розгалуженому колу і містку СD. Змінюючи опір магазину, можна досягти того, щоб по містку СD струм не йшов. В цьому випадку потенціали точок С і D будуть однакові. Однаковими будуть також і різності потенціалів між точками А і С, А і D. Із закону Ома (9.2) випливає
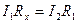, (9.6)
де І1 та І2 – сила струму на ділянках АС і АD, відповідно.
Аналогічно, з однаковості різності потенціалів між точками С і В, D і В випливає, що
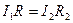. (9.7)
Поділивши (9.6) на (9.7), отримуємо
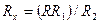, (9.8)
де R1 і R2 – опори ділянок дроту реохорду зліва і справа від його движка (ковзаючого контакту).
Опір дроту знаходиться за формулами
, 
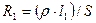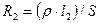, (9.9)
де ρ – питомий опір матеріалу дроту, S – площина його перетину, l1 і l2 – довжини плечей реохорду (відстань від кінців реохорду до його движка). Тоді з формул (9.8), (9.9) знаходимо, що
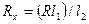. (9.10)
Експериментальна частина
1. Зібрати схему (рис. 9.1), використавши в якості Rx один з невідомих опорів, що є в наявності.
2. Движок поставити посередині реохорду на поділку 50,0.
3. Після перевірки схеми викладачем за допомогою магазину опорів підібрати такий опір R, при якому стрілка гальванометра стане на нуль (коли ключ К замкнений). Це значення R, а також l1 і l2, занести в перший рядок таблиці 9.1.
4. Змістити движок реохорду на поділку 30,0 і знову, змінюючи опір магазину, знайти значення, що відповідає нульовому струму. Значення R, l1 і l2 занести в другий рядок таблиці.
5. Встановити движок на поділку 70,0, знайти значення R і занести його в третій рядок таблиці разом з l1 і l2.
6. Такі ж самі виміри провести і для другого невідомого опору, а потім також для послідовно і паралельно з’єднаних опорів Rx1 і Rx2. Результати всіх вимірів занести в таблицю 9.1.
Таблиця 9.1
| Опір | Номер виміру i | Результати вимірів | Rx(i), Ом | Rx(cp), Ом | ||
| R(і), Ом | l1(і), м | l2(і), м | ||||
| Rx1 | ||||||
| Rx2 | ||||||
| Послідовне з’єднання Rx посл | ||||||
| Паралельне з’єднання Rx пар | ||||||
7. За даними таблиці 9.1, користуючись формулою (9.10), розрахувати Rx(i), а також середнє значення Rx(cp) для обох невідомих опорів та їх послідовного і паралельного з’єднання. Занести результати у відповідні стовпчики таблиці 9.1.
8. Користуючись значеннями Rx1(cp) і Rx2(cp), розрахувати опір їх послідовного та паралельного з’єднання за формулами
Rпосл = Rx1(cp) + Rx2(cp), Rпар = Rx1(cp) Rx2(cp) /(Rx1(cp) + Rx2(cp)). (9.11)
Порівняти результати цих розрахунків з результатами безпосередніх вимірів Rx посл(cp), Rx пар(cp) ( див. таблицю 9.1).
9. Оцінити похибку визначення опорів методом містка Уітстона, наприклад, за результатами вимірювань Rx1.
Контрольні запитання
1. Що таке сила струму, потенціал і напруга?
2. Дати визначення електрорушійної сили (ЕРС).
3. Сформулювати закон Ома для однорідної ділянки кола.
4. Сформулювати закон Ома для замкненого кола.
5. В чому полягає перше правило Кирхгофа?
6. Яке друге правило Кирхгофа?
7. Намалювати схему містка Уітстона і пояснити, як за його допомогою можна визначити невідомий опір.
8. Пояснити, чому при відсутності струму крізь гальванометр падіння напруги на ділянках АС і АD однакове.
9. Дати пояснення, чому, коли гальванометр показує нуль, струм крізь опори R і Rx однаковий?
Література
1. Трофимова Т.А. Курс физики. М.: Высшая школа, 1999.
2. Савельев И.В. Курс общей физики. -М.: Наука, 1989. §§ 35, 36.
3. Детлаф А.А., Яворский Б.М. Курс физики. -М: Высшая школа, 1989.
Інструкція складена проф. кафедри фізики Лоскутовим С.В.
Рецензент: доц. кафедри фізики Єршов А.В.
ЛАБОРАТОРНА РОБОТА № 23
ДОСЛІДЖЕННЯ ЕЛЕКТРОСТАТИЧНОГО ПОЛЯ
НА МОДЕЛІ
Мета роботи: побудувати еквіпотенціальні та силові лінії електростатичного поля та розрахувати його напруженість.
Прилади і обладнання: джерело живлення, потенціометр, панель з електродами та електропровідним папером, зонд, осцилограф.
Теоретична частина
Електростатичне поле створюється нерухомими електричними зарядами і визначається в кожній точці простору силою, що діє на пробний заряд.
Головна характеристика електростатичного поля – його напруженість:
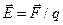, (10.1)
де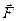 
– сила, яка діє на точковий заряд q, внесений в дану точку простору.
Енергетичною характеристикою електростатичного поля є електростатичний потенціал U. Він визначається роботою, яку виконує електрична сила при переміщенні одиничного позитивного заряду з даної точки в нескінченність.
Коли заряд переміщується з довільної точки 1 в довільну точку 2, виконана при цьому робота не залежить від траєкторії і визначається тільки різницею потенціалів:
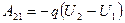. (10.2)
Потенціал є функцією координат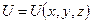 
. Якщо розподіл потенціалу відомий, можна знайти напруженість:
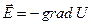, (10.3)
де оператор grad в правій частині називається градієнтом. Він діє на скалярну функцію координат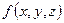 
за правилом:
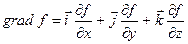, (10.4)
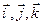є одиничні вектори вздовж осей x, y і z, відповідно.
Електростатичне поле можна зобразити за допомогою еквіпотенціальних поверхонь (еквіпотенціальних ліній в двохвимірному випадку). Еквіпотенціальна поверхня (лінія) – це геометричне місце точок однакового потенціалу.
Для зображення електростатичного поля можна також використати силові лінії (лінії напруженості). Силовою лінією називається лінія, дотична до якої в кожній точці співпадає з вектором напруженості. При побудові силових ліній можна використати такі їх властивості:
а) силові лінії починаються на позитивних зарядах і закінчуються на негативних (або розсіюються в нескінченності);
б) силові лінії при перетині еквіпотенціальних поверхонь (ліній) спрямовані перпендикулярно до них;
в) оскільки заряджені металеві поверхні є еквіпотенціальними, силові лінії виходять (або входять) перпендикулярно до електродів;
г) силові лінії розташовані густіше в тих місцях, де більше напруженість;
д) силові лінії спрямовані в бік зменшення потенціалу.
Існує аналогія між розподілом потенціалу електростатичного поля в однорідному діелектричному середовищі та розподілом потенціалу в однорідному провіднику з електричним струмом. Це можна пояснити тим, що обидва випадки описуються тим же самим рівнянням, яке не включає жодного параметру середовища
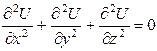. (10.5)
Це рівняння може бути застосоване до діелектрика так же само, як до провідника. Можна вивчати електричне поле в діелектрику шляхом вимірювання розподілу потенціалу в провіднику, хоч цей розподіл потенціалу має зовсім інше походження.
Експериментальна частина
Розподіл потенціалу в тонкому провідному шарі використовується в цій роботі в якості двохвимірної моделі електростатичного поля. Для вимірювання потенціалу використовується місткова схема (рис. 10.1). Два металічних електроди А і В притиснуті до аркуша паперу з провідним шаром. Напруга Uo = 6,3 В від джерела живлення подається на електроди і на нижні клеми потенціометра. До рухомого контакту S через клеми вертикального відхилення осцилографа (вхід Y) приєднується зонд P.
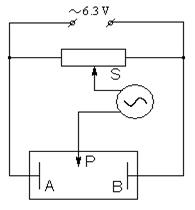
В роботі осцилограф використовується в якості індикатору наявності різниці потенціалів. Коли зонд доторкається поверхні провідного паперу, на осцилографі спостерігається сигнал (у вигляді вертикального відрізку, висота якого пропорційна різниці потенціалів між точкою дотику зонда та контактом S). Коли потенціал в точці дотику дорівнюватиме потенціалу на рухомому контакті, на екрані будемо спостерігати точку.
Рисунок 10.1
На початку роботи під електроди та провідний папір вміщують два-три аркуші паперу, на кожному з яких олівцем обведено по контуру електроди, притиснуті в тому положенні, в якому вони будуть знаходитись під час роботи.
Будемо вважати, що потенціал точки А дорівнює нулю UА = 0. Тоді UВ = 6,3 В (приймається до уваги тільки амплітудне значення потенціалу). Для того, щоб отримати еквіпотенціальну лінію для певного значення потенціалу 0 < Ui < 6,3 В, треба спочатку перевести рухомий контакт S у відповідне положення di:
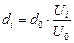, (10.6)
де d0 – довжина робочої частини потенціометра (намотки). Далі необхідно переміщувати зонд по поверхні провідного паперу у напрямку зменшення сигналу і зупинити його, коли сигнал буде дорівнювати нулю. Потенціал в точці зупинки дорівнює Ui . Щоб зафіксувати положення цієї точки, треба проколоти папір гострим кінцем зонда.
Поряд з цією точкою треба знайти ще одну точку з потенціалом Ui і зафіксувати її, щоб, послідовно переміщуючись від однієї точки до іншої, отримати низку проколів на аркушах паперу, за якими можна потім побудувати еквіпотенціальну лінію, коли аркуші буде вийнято.
1. Отримати еквіпотенціальні лінії, задаючи значення потенціалу від 0 до 6,3 В з кроком 0,9 В. Прийняти до уваги, що контури електродів є еквіпотенціальними лініями, що відповідають значенням потенціалу 0 і 6,3 В.
2. Побудувати систему силових ліній (кількістю не менше, ніж 7).
3. Визначити величину і напрямок напруженості поля в кількох точках, які задає викладач. Величину напруженості можна знайти за наближеною формулою
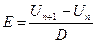, (10.7)
де Un і Un+1 є значення потенціалу двох еквіпотенціальних ліній, найближчих до точки, в якій визначається напруженість; D – довжина найкоротшого відрізку, що з’єднує ці лінії і проходить крізь дану точку.
4. Оцінити помилку, з якою визначено положення еквіпотенціальних ліній, за формулою
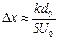, (10.8)
де k (В/поділку) – положення дільника на вході Y осцилографа.
Контрольні запитання та вправи
1. Дайте визначення напруженості та потенціалу електростатичного поля. В яких одиницях вимірюються ці величини?
2. Як зв'язані між собою напруженість поля і потенціал?
3. Чому поверхня провідника є еквіпотенціальною?
4. Які лінії називаються силовими? Які їх властивості?
5. Доведіть, що силові лінії перпендикулярні до еквіпотенціальних поверхонь.
6. Сформулюйте теорему Остроградського-Гауса.
7. Покажіть, що потенціал точкового заряду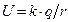 
задовольняє рівнянню (10.5).
8. Отримайте наближене співвідношення (10.7) з точної формули (10.3).
9. Підтвердить, що помилка в положенні еквіпотенціальних ліній може бути оцінена за формулою (10.8).
Література
1. Трофимова Т.А. Курс физики. -М.: Высшая школа, 1999, §§ 77-86.
2. Савельев И.В. Курс общей физики. -М.: Высшая школа, 1998, т. II, §§ 1.1-1.14.
3. Зисман Г.А., Тодес О.М. Курс общей физики. -М.: Наука, 1972, т. II, §§1.4-1.8.
4. Детлаф А.А., Яворский Б.М. Курс физики. -М: Высшая школа, 1989. §§ 13.1-13.5
.
Інструкція складена ст. викл. каф. фізики Денисовою О.І.,
відредагована доц. каф. фізики Курбацьким В.П.
Рецензент: доц. кафедри фізики Єршов А.В.
LABORATORY WORK № 23