Прохождение электронов через поглотитель.

Пусть на толстую пластинку (рис.1) нормально падает узкий пучок электронов. Вблизи границы быстрые электроны проходят в поглотителе некоторое расстояние приблизительно по прямой линии, теряя небольшое количество энергии и рассеиваясь лишь на малые углы. По мере уменьшения энергии электронов их рассеяние становится более сильным: угловое распределение электронов в пучке приближается к

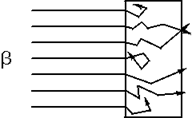
Рис.1.

гауссовскому, характерному для многократного рассеяния.

При дальнейшем рассеянии угловое распределение становится настолько размытым, что нельзя говорить о каком-нибудь преимущественном направлении движения электронов. Их распространение можно рассматривать как диффузию.

Число электронов, прошедших через фольгу, будет монотонно убывающей функцией толщины фильтра. Для умеренных толщин уменьшение числа электронов является следствием, главным образом, обратной диффузии электронов, которые отклоняются на углы, превышающие 90˚. По мере того, как толщина фильтра возрастает, уменьшается не только число прошедших фольгу электронов, но и их энергия. При значительном увеличении толщины пластинки уменьшение числа электронов происходит как вследствие рассеяния, так и по причине того, что некоторая их часть тормозится практически до нулевой энергии и выбывает из пучка.

Предельная толщина вещества, практически полностью задерживающая первоначально падающие электроны, называется эффективным, или максимальным пробегом электронов R_э. Величина R_э определяется экспериментально по кривым поглощения. Пробег электронов измеряется как в единицах длины (см), так и в массовых единицах длины (г/см²), причем

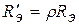
Массовая толщина вещества численно равна массе пластинки площадью в 1 см²

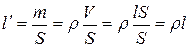, (г/см²).

Прохождение электронов через поглотитель моноэнергетических β-частиц.

Экспериментально кривые поглощения моноэнергетических электронов можно получить при измерении интенсивности β-частиц, прошедших через поглотитель переменной толщины. Схема экспериментальной установки приведена на рис.2. Результаты эксперимента с алюминием представлены на рис.3.

Каждая кривая имеет после начальной выпуклой части довольно длинную прямолинейную часть с некоторым “хвостом” на конце. За эффективный пробег электронов принимают экстраполированный пробег R_э, отмеченный на рисунке стрелочками. Экстраполированный пробег применяется для практических целей определения энергии электронов (метод поглощения для определения энергии β-частиц).

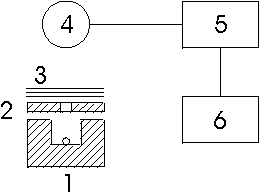
Рис. 2. Схема экспериментальной установки.

1 – источник 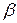- частиц, 2 – коллиматор, 3 – поглотитель, 4 – счетчик 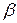-частиц, 5 – формирователь импульсов, 6 – счетчик импульсов.

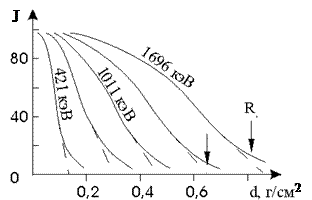Рис. 3. Кривые поглощения моноэнергетических электронов разных энергий в алюминии.

Форма кривой поглощения существенно зависит от расположения счетчика β-частиц относительно поглощающих фильтров. Это особенно заметно для малых толщин фильтров, когда число прошедших и падающих электронов практически равны. Электроны, прошедшие фильтр, имеют за счет многократного рассеяния более широкое угловое распределение. Если детектор электронов располагается не очень близко к фильтрам, то основная часть рассеянных электронов не регистрируется, и кривая поглощения будет спадающей с самого начала. Если детектор расположен к фильтрам настолько близко, что регистрирует все рассеянные электроны, то кривая поглощения будет иметь на значительном протяжении практически горизонтальный ход.

Прохождение через поглотитель β-излучения, имеющего непрерывный энергетический спектр.

Электроны, возникающие при β-радиоактивности химических изотопов, имеют непрерывный энергетический спектр с максимальной энергией Еmax. Кривые поглощения для β-излучения с непрерывным энергетическим спектром резко отличаются по форме от кривых поглощения для моноэнергетических электронов и имеют приблизительно экспоненциальный ход. Качественно начальную часть кривой можно объяснить тем, что в пучке β-частиц имеются электроны всевозможных энергий, в том числе и очень малых. Медленные же электроны поглощаются весьма сильно. Конец кривой поглощения асимптотически подходит к линии фона. Это объясняется постоянно уменьшающимся в β-спектре числом быстрых электронов и относительно слабым поглощением электронов максимальной энергии.

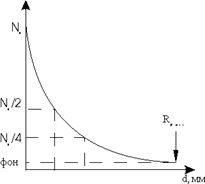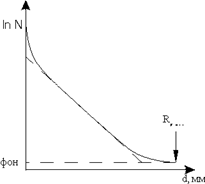Типичная кривая поглощения β-излучения, полученная по схеме на рис.2, приведена на рис.4 и 5.

Рис. 4. Рис. 5.

Кривая поглощения (рис.4) описывается экспоненциальным законом

,

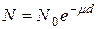где N₀ – число β-частиц до поглотителя, N – число частиц после прохождения слоя d, μ – линейный коэффициент поглощения (см ^–1).

При измерении толщины d в массовых единицах закон поглощения запишется

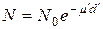
где d΄=ρd (г/см²) – массовая толщина, μ΄=μ/ρ (см²∙г^-1) – массовый коэффициент поглощения.

Необходимость введения двух коэффициентов поглощения вызвана тем, что линейный коэффициент ослабления резко зависит как от природы поглощающего вещества, так и от граничной энергии β –спектра Е_max и примерно одинаков для химических элементов с близкими значениями Z.

На практике часто используется понятие толщины слоя половинного поглощения d_½, необходимого для уменьшения вдвое начальной интенсивности β –излучения. Так как

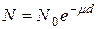и N(d_½) = N₀/2,

то d_½ = .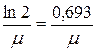

Все рассмотренные характеристики: μ, μ΄,d_½, R_max можно определить из экспериментальной кривой поглощения (рис.4 и 5).

Измерения

1. Подготовить лабораторную установку к работе, проверив работоспособность источника питания, секундомера и счетчика импульсов.

2. Снять кривую поглощения по схеме рис. 2. Фольга располагается между счетчиками излучения и коллиматором. Нужная толщина фильтра достигается путем последовательного наложения алюминиевых пластинок друг на друга. Толщина фольги измеряется микрометром. Время измерения 3-5 минут.

3. Измерить фон установки. Он складывается из действия на счетчик: 1) космического излучения; 2) рассеянных β - частиц; 3) тормозного излучения; 4) γ - лучей в спектре источника.

Для определения N_ф необходимо определить счет установки с фильтром, задерживающим все β – лучи (толщиной, например, 2мм).

4. Заполнить таблицу.

Таблица

№ п/п	Толщина пластинки (мм)	Кол-во пластинок	d, мм	Время измерения t, мин.	Счет Nэ	Счет Nф	Счет N = Nэ-Nф	Скорость счета n=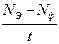

Обработка результатов.

1. Построить графики n = f(d) и ln n = f(d) с учетом погрешности измерений.

2. Определить по графикам предельный пробег электронов R_βmax.

3. Пользуясь уравнением 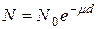рассчитать линейный коэффициент поглощения μ. По формуле 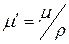рассчитать массовый коэффициент .

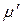4. Определить толщину слоя половинного поглощения d_1/2 .

5. По величине предельного пробега электронов R_βmax и толщине слоя половинного поглощения d_1/2 оценить предельную энергию E_max β - спектра.

6. Сравнить полученные результаты с данными, известными из литературы.

7. Оценить погрешности полученных результатов.

Контрольные вопросы и задания

1. Что называется радиоактивностью? Какие процессы относятся к числу радиоактивных?

2. Перечислите физические процессы, происходящие при взаимодействии β-излучения с веществом.

3. В чем заключаются процессы упругого рассеяния электронов ядрами, электронов на электронах?

4. Чем обусловлены потери энергии частицы при прохождении через поглощающую среду?

5. Что происходит при прохождении электрона через поглотитель?

6. Каковы особенности прохождения через поглотитель моноэнергетических β-частиц и β-излучения, имеющего непрерывный энергетический спектр?

7. Объясните физический смысл понятий: массовая толщина, линейный и массовый коэффициент поглощения, эффективный пробег β- частицы. Какова методика их измерения в данной работе?

Список рекомендуемой литературы

1. Савельев,И.В. Курс общей физики: В 3-х т / И.В.Савельев-М.: Наука, 1989, Т. 2. 496 с.; Т. 3, 304 с.

2. Детлаф,А.А., Яворский,Б.М. Курс физики / А.А.Детлаф, Б.М.Яворский-М.: Высш. шк. 1989, 607с.

3. Трофимова Т.И. Курс физики / Т.И.Трофимов-М.: Высш. шк. 1985, 380 с.

4. Лабораторный практикум по физике: Учебное пособие для студентов ВТУЗов/ Алексеев Б.Ф., Барсуков К.А., Войцеховская И.А. и др.; Под ред. К.А. Барсукова и Ю.И. Уханова-М.: Высш. шк., 1988, 351с.

Оглавление

ПОРЯДОК ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ…………………3

ЛАБОРАТОРНАЯ РАБОТА № 6.1……………………………………………4

ЛАБОРАТОРНАЯ РАБОТА № 6.2………………………………………….14

ЛАБОРАТОРНАЯ РАБОТА № 6.3………………………………………….19

ЛАБОРАТОРНАЯ РАБОТА № 6.4…………………………………………..26

ЛАБОРАТОРНАЯ РАБОТА № 6.5………………………………………….35

Список рекомендуемой литературы…………………………………………45

Физика атомов и молекул.

Ядерная физика

МЕТОДИЧЕСКИЕ УКАЗАНИЯ