Основные положения молекулярно-кинетической теории газов

1. Количество вещества однородного газа (в молях):

n = 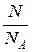или n = ,

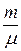где N – число молекул газа; N_A – число Авогадро; m – масса газа; m – молярная масса газа.

Если система представляет смесь нескольких газов, то количество вещества системы равно:

n = n₁+n₂+...+n_n =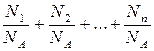

или

n = ,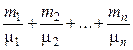

где n_i, N_i, m_i, m_i – соответственно количество вещества, число молекул, масса, молярная масса i-й компоненты смеси.

2. Уравнение Менделеева-Клапейрона (уравнение состояния идеального газа):

,

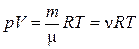где m – масса газа; m – молярная масса газа; R – универсальная газовая постоянная; n= m/m – количество вещества; T – термодинамическая температура Кельвина.

3. Опытные газовые законы, являющиеся частными случаями уравнения Менделеева-Клапейрона для изопроцессов:

а) закон Бойля-Мариотта (изотермический процесс: T = const;
m = const):

pV = const

или для двух состояний газа:

p₁V₁ = p₂V₂,

где p₁ и V₁ – давление и объем газа в начальном состоянии; p₂ и V₂ – те же величины в конечном состоянии;

б) закон Шарля (изобарический процесс: p = const, m = const):

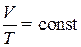
или для двух состояний:

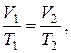
где V₁ и T₁ – объем и температура газа в начальном состоянии; V₂ и T₂ – те же величины в конечном состоянии;

в) закон Гей-Люссака (изохорический процесс – V = const,
m = const):

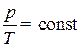
или для двух состояний:

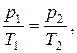
где p₁ и T₁ – давление и температура газа в начальном состоянии; p₂ и T₂ – те же величины в конечном состоянии;

г) объединенный газовый закон (m = const):

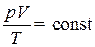
или для двух состояний:

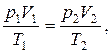
где p₁, V₁, T₁ – давление, объем и температура газа в начальном состоянии; p₂, V₂, T₂ – те же величины в конечном состоянии.

4. Закон Дальтона, определяющий давление смеси газов:

p = p₁ + p₂ +...+ p_n,

где p_i – парциальные давления компонентов смеси; n – число компонентов смеси.

5. Молярная масса смеси газов:

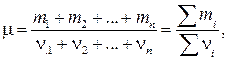
где m_i – масса i-го компонента смеси; n_i = m_i/m_i – количество вещества i-го компонента смеси; n – число компонентов смеси.

6. Массовая доля w_i i-го компонента смеси газа (в долях единицы или процентах):

,

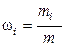где m – масса смеси.

7. Концентрация молекул (число молекул в единице объема):

,

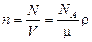где N – число молекул, содержащихся в данной системе; r – плотность вещества. Формула справедлива не только для газов, но и для любого агрегатного состояния вещества.

8. Основное уравнение молекулярно-кинетической теории газов:

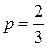náЕ_постñ,

где áЕ_постñ – средняя кинетическая энергия поступательного движения молекулы.

9. Средняя кинетическая энергия поступательного движения молекулы:

áЕ_постñ = 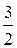kT,

где k – постоянная Больцмана.

10. Средняя полная кинетическая энергия молекулы:

áЕñ = 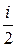kT,

где i – число степеней свободы молекулы.

11. Зависимость давления газа от концентрации молекул и температуры:

p = nkT.

12. Скорости молекул:

средняя квадратичная ;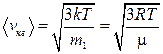

средняя арифметическая ;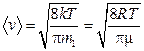

наиболее вероятная ,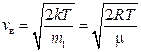

где m₁ – масса одной молекулы.

13. Относительная скорость молекулы:

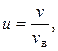
где v – скорость данной молекулы.

14. Распределение скоростей молекул по Максвеллу:

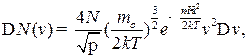
где DN(v) – число молекул, скорости которых лежат в интервале от v до v + Dv.

15. Барометрическая формула:

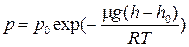
или

,

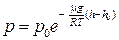где р и р₀ – давление газа на высоте h и h₀.

16. Распределение Больцмана:

,

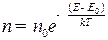где n₀ и Е₀ – концентрация и потенциальная энергия частиц на высоте h₀.

17. Средняя длина свободного пробега молекул:

,

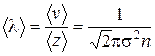где <v> – средняя арифметическая скорость, <z> – среднее число столкновений каждой молекулы с остальными в единицу времени, s – эффективный диаметр молекулы, n – число молекул в единице объема (концентрация молекул). Общее число столкновений всех молекул в единице объема за единицу времени Z = <z> n/2.

18. Масса, перенесенная за время Dt при диффузии (закон Фика):

,

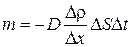где Dr/Dх – градиент плотности в направлении, перпендикулярном к площадке DS, D = <v><l>/3 – коэффициент диффузии (<v> – средняя арифметическая скорость, <l> – средняя длина свободного пробега молекул).

19. Импульс, перенесенный газом за время Dt, определяет силу внутреннего трения F_тр в газе (закон Ньютона):

,

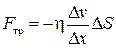где Dv/Dx – градиент скорости течения газа в направлении, перпендикулярном к площадке DS, h = <v><l>r/3 – динамическая вязкость.

20. Количество теплоты, перенесенное за время Dt вследствие теплопроводности, определяется формулой (закон Фурье):

,

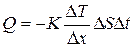где DТ/Dx – градиент температуры в направлении, перпендикулярном к площадке DS, К = <v><l>с_Vr/3 – коэффициент теплопроводности.

Основы термодинамики

21. Удельные теплоемкости газа при постоянном объеме (c_V) и при постоянном давлении (c_p):

; .

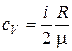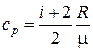22. Связь между удельной (с) и молярной (С_m) теплоемкостями:

c = C_m/m; C_m = cm.

23. Уравнение Роберта-Майера:

C_{mp –} C_mV = R.

24. Внутренняя энергия идеального газа :

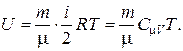
25. Первое начало термодинамики:

Q = DU + A,

где Q – теплота, сообщенная системе (газу); DU – изменение внутренней энергии системы; A – работа, совершенная системой против внешних сил.

26. Работа расширения газа:

в общем случае ;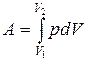

при изобарическом процессе A = p(V₂ – V₁);

при изотермическом процессе ;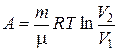

при адиабатическом процессе ,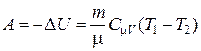

или ,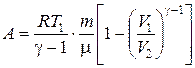

где g = с_p/c_V – показатель адиабаты.

27. Уравнения Пуассона, связывающие параметры идеального газа при адиабатическом процессе:

, ;

; .

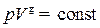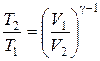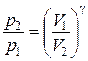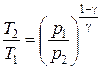28. Термический к.п.д. цикла:

,

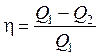где Q₁ – теплота, полученная рабочим телом от нагревателя; Q₂ – теплота, переданная телом охладителю.

29. Термический к.п.д. цикла Карно:

,

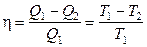где T₁ и T₂ – термодинамические температуры нагревателя и охладителя.

30. Разность энтропий S_B – S_A двух состояний В и А определяется формулой:

.

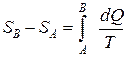Жидкости и твердые тела

31. Коэффициент поверхностного натяжения:

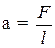или ,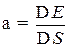

где F – сила поверхностного натяжения, действующая на контур l, ограничивающий поверхность жидкости; DE – изменение свободной энергии поверхностной пленки жидкости, связанное с изменением площади DS поверхности этой пленки.

32. Формула Лапласа, выражающая давление p, создаваемое сферической поверхностью жидкости:

,

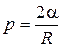где R – радиус сферической поверхности.

33. Высота подъема жидкости в капиллярной трубке:

,

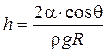где q – краевой угол (q = 0 при полном смачивании стенок трубки жидкостью; q = p при полном несмачивании); R – радиус канала трубки; r – плотность жидкости; g – ускорение свободного падения.

34. Высота подъема жидкости между двумя близкими и параллельными друг другу плоскостями:

,

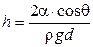где d – расстояние между плоскостями.

35. Закон Дюлонга-Пти:

С_m= 3R,

где С_m – молярная теплоемкость химически простых твердых тел,
R – универсальная газовая постоянная.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Пример 1. При выстреле из пружинного пистолета вертикально вверх пуля массой m = 20 г поднялась на высоту h = 5 м. Определить жесткость k пружины пистолета, если она была сжата на x = 10 см. Массой пружины пренебречь.

РЕШЕНИЕ. Воспользуемся законом сохранения энергии в механике. Но прежде проследим за энергетическими превращениями, с которыми связан выстрел. При зарядке пистолета сжимается пружина и совершается работа A₁, в результате чего пружина приобретает потенциальную энергию П₁. При выстреле потенциальная энергия пружины переходит в кинетическую энергию Т₂ пули, а затем при подъеме ее на высоту h превращается в потенциальную энергию П₂ пули.

Если пренебречь потерями энергии в этой «цепочке» энергетических превращений, то на основе закона сохранения энергии можно записать:

A₁ = П₂. (1)

Найдем работу А₁. Сила F₁, сжимающая пружину, является переменной: в каждый момент она по направлению противоположна силе упругости F и численно равна ей. Сила упругости, возникающая в пружине при ее деформации, определяется по закону Гука: F = kx, где x – абсолютная деформация пружины.

Работу переменной силы вычислим как сумму элементарных работ. Элементарная работа при сжатии пружины на dx выразится формулой dA₁ = F₁dx, или dA₁ = kx× dx. Интегрируя в пределах от 0 до x, получим:

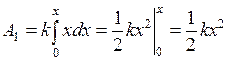. (2)

Потенциальная энергия пули на высоте h определится по формуле:

П₂ = mgh, (3)

где g – ускорение свободного падения.

Подставив в (1) выражение A₁ из (2) и П ₂ из (3), найдем

,

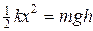откуда

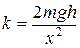. (4)

Проверим, дает ли полученная формула единицу жесткости k. Для этого в правую часть формулы (4) вместо величин подставим их единицы:

.

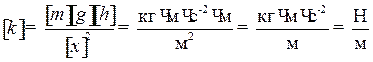Убедившись, что полученная единица Н/м является единицей жесткости, подставим в формулу (4) значения величин и произведем вычисления:

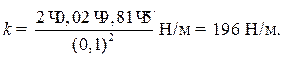
Пример 2.Через блок в виде сплошного диска, имеющего массу m = 80 г (рис.1), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m₁ = 100 г и m ₂ = 200 г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением и массой нити пренебречь.

РЕШЕНИЕ. Воспользуемся основными уравнениями динамики поступательного и вращательного движений. Для этого рассмотрим силы, действующие на каждый груз в отдельности и на блок. На первый груз действуют две силы: сила тяжести 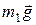и сила упругости (сила натяжения нити) 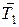. Спроецируем эти силы на ось x, которую направим вниз, и напишем уравнение движения (второй закон Ньютона) в координатной форме:

m₁g – T₁ = – m₁a. (1)

Уравнение движения для второго груза запишется аналогично:

m₂g – T₂ = m₂a. (2)

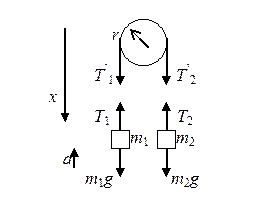
Рис. 1.

Под действием двух моментов сил Tr и Tr относительно оси, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение e (e = a/r). Согласно основному уравнению динамики вращательного движения

Tr – Tr = J_ze, (3)

где 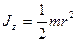– момент инерции блока (сплошного диска) относительно оси z.

Сила T согласно третьему закону Ньютона по абсолютному значению равна силе T₁. Соответственно сила T по абсолютному значению равна силе T₂. Воспользовавшись этим, подставим в уравнение (3) вместо Tи T выражения для T₁ и T₂, получив их предварительно из уравнений (1) и (2):

.

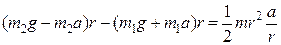После сокращения на r и перегруппировки членов найдем интересующее нас ускорение:

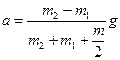. (4)

Отношение масс в правой части формулы (4) есть величина безразмерная. Поэтому массы m₁, m₂ и m можно выразить в граммах, как они даны в условии задачи. Ускорение g надо выразить в единицах СИ. После подстановки получим:

.

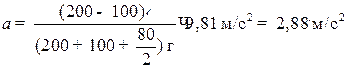Пример 3. Платформа в виде сплошного диска радиусом R = 1,5 м и массой m₁= 180 кг вращается по инерции около вертикальной оси с частотой n = 10 мин^-1. В центре платформы стоит человек массой m₂ = 60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?

РЕШЕНИЕ. Платформа вращается по инерции. Следовательно, момент внешних сил относительно оси вращения z, совпадающей с геометрической осью платформы, равен нулю. При этом условии момент импульса L_z системы платформа – человек остается постоянным:

L_z = J_z w = 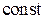, (1)

где J_z – момент инерции платформы с человеком относительно оси z; w – угловая скорость платформы.

Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому J_z = J₁ + J₂, где J₁ – момент инерции платформы; J₂ – момент инерции человека.

С учетом этого равенство (1) примет вид:

(J₁ + J₂)w = ,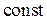

или

(J₁ + J₂)w = (J+J)w¢, (2)

где значения моментов инерции J₁ и J₂ относятся к начальному состоянию системы; J и J к конечному.

Момент инерции платформы относительно оси z при переходе человека не изменяется: J₁ = J = 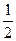m₁R². Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции J₂ в начальном положении (в центре платформы) можно считать равным нулю. В конечном положении (на краю платформы) момент инерции человека J = m₂R². Подставим в формулу (2) найденные выражения моментов инерции, а также выразим начальную угловую скорость w вращения платформы с человеком через частоту вращения n (w = 2pn) и конечную угловую скорость w¢ – через линейную скорость 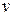человека относительно пола (w¢= 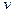/R):

.

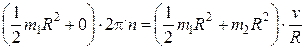После сокращения на R² и простых преобразований находим интересующую нас скорость:

.

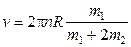Учитывая, что n = 10 мин ^-1 = 1/6 с ^-1, подставим числовые значения физических величин в СИ и произведем вычисления:

.

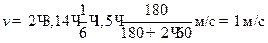Пример 4. В сосуде объемом 20 л находится 4 г водорода при температуре 27°С. Найти давление водорода.

РЕШЕНИЕ. Идеальные газы подчиняются уравнению Менделеева-Клапейрона

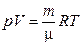, (2)

которое связывает объем газа V, его давление р, термодинамическую температуру Т и массу m. В уравнении (1) R = 8,31 Дж/(моль×К) – газовая постоянная, m – молярная масса газа, n= m/m – количество газа.

Из уравнения (1) имеем

.

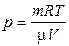Подставляя числовые данные m = 4×10^{-3 кг,} m = 0,002 кг/моль,
Т = 300 К, V = 20 л = 2×10^{-2 м3}, получим:

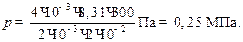
Пример 5. Найти удельную теплоемкость при постоянном объеме некоторого многоатомного газа, если известно, что плотность этого газа при нормальных условиях равна 0,795 кг/м³.

РЕШЕНИЕ. Удельная теплоемкость при постоянном объеме определяется формулой:

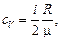(1)

где R – универсальная газовая постоянная, i – число степеней свободы молекул многоатомного газа и m – молярная масса газа.

Формулу для плотности газа нетрудно получить из уравнения Менделеева-Клапейрона:

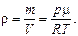(2)

Из (1) и (2) имеем:

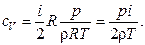(3)

Так как газ находится при нормальных условиях, то
р = 1,013×10⁵ Па, Т = 273 К. Для многоатомных газов i = 6. Подставляя числовые данные в (3), получим:

с_V = 1,4 кДж/(кг×К).

Пример 6. При изотермическом расширении азота массой 100 г, имевшего температуру 280 К, его объем увеличился в 3 раза. Найти: работу, совершенную газом при расширении; изменение внутренней энергии газа; количество теплоты, сообщенное газу.

Решение. Из уравнения Менделеева-Клапейрона находим:

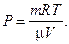
При изотермическом процессе (T = const), работа газа определяется по формуле

.

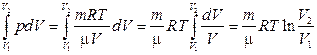Молярная масса азота m = 28∙10^-3 кг/моль, V₂/V₁ = 3, m = 0,1 кг,
R = 8,31 Дж/(моль∙К). Подставив в последнюю формулу числовые значения, получим A = 9,13 кДж.

Изменение внутренней энергии ∆U = 0, так как T = const. Следовательно, согласно первому закону термодинамики, сообщенное газу количество теплоты Q = A = 9,13 кДж.

КОНТРОЛЬНАЯ РАБОТА № 1

Студент-заочник должен решить восемь задач варианта, указанного в таблице, номер которого совпадает с двумя последними цифрами его зачетной книжки.

Таблица 1

Вариант	Номера задач
	1.8	1.36	1.58	1.69	2.14	2.21	2.57	2.67
	1.13	1.24	1.49	1.76	2.14	2.37	2.41	2.74
	1.20	1.32	1.43	1.76	2.11	2.26	2.53	2.61
	1.2	1.21	1.46	1.68	2.6	2.30	2.57	2.77
	1.16	1.30	1.54	1.64	2.14	2.25	2.42	2.65
	1.17	1.35	1.43	1.72	2.19	2.21	2.56	2.66
	1.19	1.21	1.55	1.64	2.13	2.35	2.51	2.77
	1.4	1.30	1.50	1.69	2.11	2.34	2.46	2.79
	1.15	1.38	1.56	1.72	2.10	2.30	2.57	2.61
	1.3	1.29	1.52	1.61	2.20	2.24	2.58	2.80
	1.15	1.24	1.46	1.68	2.18	2.32	2.60	2.67
	1.8	1.39	1.58	1.67	2.20	2.39	2.53	2.68
	1.18	1.26	1.59	1.65	2.17	2.28	2.43	2.64
	1.6	1.32	1.56	1.76	2.15	2.27	2.56	2.77
	1.14	1.29	1.57	1.74	2.13	2.40	2.55	2.77
	1.5	1.31	1.59	1.72	2.7	2.24	2.49	2.77
	1.18	1.32	1.45	1.65	2.6	2.27	2.57	2.70
	1.13	1.25	1.43	1.67	2.8	2.28	2.43	2.61
	1.4	1.38	1.56	1.75	2.3	2.30	2.59	2.75
	1.17	1.39	1.55	1.76	2.11	2.33	2.48	2.80
	1.14	1.28	1.50	1.65	2.9	2.26	2.42	2.68
	1.14	1.31	1.48	1.75	2.3	2.34	2.43	2.65
	1.1	1.33	1.41	1.77	2.10	2.34	2.60	2.74
	1.18	1.32	1.42	1.73	2.6	2.28	2.59	2.80
	1.10	1.21	1.49	1.63	2.17	2.37	2.45	2.76
	1.7	1.26	1.50	1.67	2.13	2.25	2.48	2.66
	1.17	1.27	1.58	1.80	2.20	2.34	2.49	2.74
	1.18	1.36	1.42	1.65	2.14	2.26	2.43	2.73
	1.1	1.32	1.44	1.63	2.12	2.39	2.41	2.79
	1.10	1.33	1.41	1.67	2.1	2.37	2.53	2.64
	1.7	1.28	1.43	1.79	2.19	2.24	2.45	2.69
	1.5	1.40	1.56	1.74	2.17	2.39	2.46	2.80
	1.13	1.40	1.45	1.78	2.16	2.30	2.42	2.66
	1.14	1.38	1.45	1.64	2.5	2.38	2.52	2.75
	1.12	1.26	1.52	1.66	2.4	2.24	2.54	2.70
	1.11	1.36	1.42	1.74	2.17	2.22	2.49	2.70
	1.14	1.32	1.59	1.62	2.17	2.25	2.59	2.80
	1.17	1.29	1.54	1.76	2.2	2.37	2.45	2.68
	1.5	1.22	1.53	1.66	2.7	2.38	2.56	2.77
	1.5	1.34	1.51	1.65	2.12	2.24	2.44	2.75

Продолжение табл. 1

	1.1	1.33	1.51	1.75	2.5	2.35	2.58	2.63
	1.13	1.27	1.56	1.62	2.2	2.30	2.59	2.76
	1.8	1.25	1.60	1.63	2.18	2.33	2.58	2.61
	1.6	1.36	1.51	1.65	2.6	2.40	2.56	2.70
	1.13	1.37	1.41	1.71	2.18	2.39	2.48	2.71
	1.2	1.21	1.48	1.67	2.7	2.38	2.49	2.78
	1.5	1.23	1.52	1.77	2.20	2.27	2.43	2.76
	1.17	1.30	1.41	1.80	2.2	2.23	2.58	2.75
	1.10	1.36	1.45	1.62	2.9	2.36	2.59	2.68
	1.14	1.29	1.41	1.80	2.4	2.31	2.59	2.65
	1.13	1.22	1.45	1.65	2.2	2.24	2.58	2.62
	1.14	1.35	1.45	1.69	2.1	2.31	2.55	2.72
	1.14	1.30	1.41	1.62	2.9	2.27	2.57	2.62
	1.1	1.35	1.55	1.74	2.2	2.37	2.44	2.80
	1.9	1.38	1.58	1.61	2.18	2.32	2.46	2.78
	1.7	1.21	1.49	1.68	2.2	2.36	2.60	2.65
	1.4	1.37	1.46	1.80	2.4	2.36	2.54	2.78
	1.9	1.40	1.51	1.61	2.20	2.26	2.60	2.77
	1.11	1.38	1.60	1.79	2.15	2.37	2.52	2.73
	1.13	1.37	1.45	1.77	2.18	2.29	2.49	2.64
	1.17	1.26	1.54	1.66	2.7	2.28	2.58	2.69
	1.2	1.30	1.54	1.74	2.6	2.26	2.56	2.79
	1.19	1.36	1.51	1.73	2.10	2.29	2.50	2.64
	1.20	1.26	1.56	1.64	2.12	2.29	2.60	2.67
	1.18	1.39	1.60	1.64	2.10	2.25	2.41	2.73
	1.8	1.22	1.44	1.64	2.5	2.22	2.49	2.64
	1.11	1.27	1.48	1.65	2.9	2.40	2.44	2.76
	1.19	1.31	1.43	1.76	2.6	2.23	2.41	2.65
	1.6	1.22	1.50	1.66	2.20	2.27	2.42	2.68
	1.4	1.25	1.43	1.71	2.7	2.38	2.41	2.78
	1.4	1.40	1.41	1.77	2.6	2.37	2.42	2.71
	1.2	1.25	1.52	1.63	2.7	2.23	2.46	2.75
	1.20	1.33	1.41	1.70	2.4	2.30	2.58	2.62
	1.4	1.40	1.52	1.64	2.3	2.23	2.49	2.61
	1.17	1.37	1.41	1.66	2.6	2.40	2.42	2.68
	1.4	1.39	1.52	1.80	2.6	2.24	2.46	2.77
	1.20	1.25	1.44	1.65	2.11	2.33	2.58	2.76
	1.16	1.23	1.59	1.71	2.11	2.23	2.59	2.67
	1.6	1.36	1.49	1.69	2.15	2.26	2.45	2.71
	1.14	1.23	1.42	1.64	2.20	2.32	2.55	2.64
	1.18	1.40	1.55	1.73	2.14	2.40	2.41	2.76
	1.16	1.33	1.47	1.68	2.18	2.36	2.47	2.61
	1.11	1.39	1.50	1.72	2.18	2.26	2.48	2.62
	1.6	1.27	1.53	1.67	2.6	2.36	2.51	2.76
	1.9	1.22	1.55	1.61	2.13	2.21	2.50	2.70
	1.15	1.38	1.57	1.62	2.10	2.38	2.58	2.79

Окончание табл. 1

	1.20	1.37	1.55	1.77	2.9	2.21	2.51	2.79
	1.8	1.34	1.52	1.74	2.14	2.30	2.43	2.69
	1.11	1.36	1.48	1.74	2.1	2.38	2.53	2.69
	1.17	1.33	1.52	1.62	2.12	2.34	2.51	2.65
	1.19	1.27	1.49	1.73	2.20	2.27	2.43	2.80
	1.5	1.25	1.48	1.64	2.17	2.21	2.50	2.65
	1.16	1.27	1.60	1.64	2.13	2.22	2.51	2.72
	1.12	1.21	1.54	1.76	2.9	2.31	2.41	2.75
	1.11	1.37	1.43	1.66	2.19	2.33	2.55	2.61
	1.15	1.33	1.42	1.77	2.9	2.21	2.46	2.69
	1.14	1.27	1.46	1.71	2.18	2.28	2.58	2.76
	1.9	1.31	1.41	1.73	2.2	2.26	2.45	2.66
	1.9	1.33	1.57	1.66	2.17	2.37	2.50	2.72

1.1. По ледяной горке пустили скользить снизу вверх шайбу. На расстоянии l = 3 м от начальной точки шайба побывала дважды: через t₁ = 2 c и t₂ = 10 с после начала движения. Считая ускорение постоянным, найти его модуль и начальную скорость шайбы.

1.2. Тело движется равноускоренно с начальной скоростью v₀. Определить ускорение тела, если за время t = 2 c оно прошло путь s = 16 м и его скорость v = 3v₀.

1.3. При падении камня в колодец его удар о поверхность воды доносится через t = 5 с. Принимая скорость звука равной v = 330 м/с, определить глубину колодца.

1.4. Тело, брошенное вертикально вверх, вернулось на землю через 3 с. Какова была начальная скорость v₀ тела и на какую высоту h оно поднялось? Сопротивление воздуха не учитывать.

1.5. С башни высотой H = 25 м горизонтально брошен камень со скоростью v₀ = 15 м/c. Найти: 1) сколько времени камень будет двигаться; 2) на каком расстоянии s_x от основания башни он упадет на землю; 3) с какой скоростью v он упадет на землю; 4) какой угол j составит траектория камня с горизонтом в точке его падения.

1.6. Камень брошен горизонтально со скоростью v₀ = 15 м/c. Найти нормальное а_n и тангенциальное a_t ускорения камня через время t = 1 c после начала движения. Сопротивление воздуха не учитывать.

1.7. Мяч брошен со скоростью v₀ = 10 м/c под углом a= 40° к горизонту. Найти: 1) на какую высоту s_y поднимется мяч; 2) на каком расстоянии s_x от места бросания он упадет на землю, 3) сколько времени он будет двигаться. Сопротивление воздуха не учитывать.

1.8. Тело брошено со скоростью v₀ под углом к горизонту. Время полета t = 2,2 c. На какую высоту h поднимется тело.

1.9. Тело брошено под углом a к горизонту. Оказалось, что максимальная высота подъема h = 1/4 s (s – дальность полета). Определить угол, под которым тело бросили. Сопротивление воздуха не учитывать.

1.10. Тело начинает двигаться по окружности радиусом R = 30 м с постоянным по модулю тангенциальным ускорением а_t = 5 м/с². Найти полное ускорение тела через t = 3 с после начала движения.

1.11.Чему равен коэффициент трения колес автомобиля о дорогу, если при скорости автомобиля v = 10 м/с тормозной путь равен
s = 8,0 м?

1.12.На горизонтальной поверхности лежит тело массой 5,0 кг. Какой путь пройдет это тело за t = 1 с, если к нему приложить силу
F = 50 H, образующую угол a = 60° с горизонтом? Коэффициент трения между телом и поверхностью m = 0,10.

1.13.Тело скользит по наклонной плоскости, составляющей с горизонтом угол a = 45°. Пройдя путь s = 36,4 см, тело приобретает скорость v = 2 м/с. Чему равен коэффициент трения тела о плоскость?

1.14. По наклонной плоскости с углом a наклона к горизонту, равным 30°, скользит тело. Определить скорость тела в конце второй секунды от начала скольжения, если коэффициент трения m = 0,15.

1.15. Канат лежит на столе так, что часть его свешивается со стола, и начинает скользить тогда, когда длина свешивающейся составляет 25% всей его длины. Чему равен коэффициент трения каната о стол?

1.16. Два тела массами m₁=0,8 кг и m ₂= 1,5 кг связаны невесомой нерастяжимой нитью, переброшенной через невесомый блок, и находятся на наклонных плоскостях, которые составляют с горизонтом углы a = 15° и b = 30°. Коэффициент трения тел о плоскости одинаков и равен m =0,1. Найти ускорение, с которым движутся тела, и силу натяжения нити.

1.17.Два тела одинаковой массы m₁ = m ₂ =1 кг связаны невесомой нерастяжимой нитью, перекинутой через невесомый блок. Тело 1 находится на наклонной плоскости, составляющей с горизонтом угол a = 30°, а тело 2 свешивается вертикально. Считая нить и блок невесомыми и не учитывая трение в оси блока, найти силу давления на ось. Коэффициент трения между наклонной плоскостью и телом, лежащим на ней, m = 0,1.

1.18.Два груза массами m₁= 4,0 кг и m ₂= 1,0 кг связаны нитью, перекинутой через невесомый блок, который прикреплен к вершине призмы, и могут скользить по граням этой призмы. Найти ускорение грузов, если грани призмы образуют с горизонтом углы a = 60° и b = 30°, а коэффициент трения m = 0,20.

1.19.Две гири массами m₁= 2 кг и m ₂= 1 кг соединены нитью, перекинутой через блок. Найти: 1) ускорение а, с которым движутся гири; 2) натяжение нити Т. Трение в блоке не учитывать.

1.20.Через невесомый блок, подвешенный к пружинным весам, перекинута нерастяжимая легкая нить, к концам которой прикреплены грузы массами m₁= 0,5 кг и m ₂= 0,6 кг. Что покажут весы во время движения грузов? Трение в блоке не учитывать.

1.21.Камень, привязанный к веревке, равномерно вращается в вертикальной плоскости. Разность между максимальным и минимальным натяжением веревки DF_н= 9,8 H. Найти массу камня.

1.22.Груз, привязанный к шнуру длиной l = 50 см, описывает окружность в горизонтальной плоскости. Какой угол j образует шнур с вертикалью, если частота вращения n = 1 c^-1?

1.23.Груз, привязанный к нити длиной l = 50 см, описывает окружность в горизонтальной плоскости. Найти период T обращения, если нить отклонена на угол j = 60° от вертикали.

1.24.Шарик, подвешенный на легкой нерастяжимой нити длиной l = 0,5 м, вращается в горизонтальной плоскости. Нить образует с вертикалью угол a = 30°. Найти период вращения шарика.

1.25.Планета массой M движется по окружности вокруг Солнца со скоростью v. Определить период обращения этой планеты вокруг Солнца.

1.26.Период обращения искусственного спутника Земли составляет 3 часа. Считая его орбиту круговой, определить, на какой высоте от поверхности Земли находится спутник.

1.27.Определить значение первой космической скорости, т.е. наименьшей скорости, которую необходимо сообщить телу, чтобы его орбита в поле тяготения Земли стала круговой (тело могло превратиться в искусственный спутник Земли).

1.28.Искусственный спутник вращается вокруг Земли по окружности на высоте h = 3,6 Мм. Найти линейную скорость v спутника. Радиус R Земли и ускорение свободного падения g на поверхности Земли считать известными.

1.29.Период T обращения искусственного спутника Земли составляет 2 ч. Считая его орбиту круговой, определить, на какой высоте h от поверхности Земли движется спутник.

1.30.Найти массу Земли, если известно, что искусственный спутник, запущенный на высоту 1 Мм, имеет период обращения 106 мин.

1.31.Маховик в виде сплошного диска, момент инерции которого J = 150 кг×м², вертится с частотой n = 240 об/мин. Через время t = 1 мин, как на маховик стал действовать момент силы торможения, он остановился. Найти: 1) момент М сил торможения; 2) количество оборотов маховика от начала торможения до полной остановки.

1.32. Частота вращения n₀ маховика, момент инерции J которого равен 120 кг×м², составляет 240 об/мин. После прекращения действия на него вращательного момента маховик под действием сил трения в подшипниках остановился за время t =p мин. Считая трение в подшипниках постоянным, найти момент М сил трения.

1.33. На однородный сплошной цилиндрический вал радиусом R= 50 см намотана легкая нить, к концу которой прикреплен груз массой m = 6,4 кг. Груз опускается с ускорением а = 2 м/с². Найти: 1) момент инерции J вала; 2) массу m вала.

1.34. На барабан радиусом R = 10 см намотана нить, к концу которой прикреплен груз массой m = 0,5 кг. Найти момент инерции барабана, если груз опускается с ускорением а = 1,0 м/с².

1.35. Маховик массой m = 10 кг и радиусом R = 10 см свободно вертится вокруг оси, проходящей через его центр, с круговой частотой 6 с^-1. При торможении маховик останавливается через t = 5 с. Найти момент торможения.

1.36. На однородный сплошной цилиндрический вал радиусом R = 20 см, момент инерции которого J = 0,15 кг×м², намотана легкая нить, к концу которой прикреплен груз массой m = 0,5 кг. До начала вращения барабана высота груза над полом составляла h = 2,3 м. Найти: 1) время опускания груза; 2) силу натяжения нити.

1.37. Через неподвижный блок в виде однородного сплошного цилиндра массой m = 0,2 кг перекинута невесомая нить, к концам которой прикреплены тела массами m₁= 0,35 кг и m₂ = 0,55 кг. Не учитывая трение в оси блока, найти: 1) ускорение тел; 2) отношение Т₂/Т₁ сил натяжения нити.

1.38.Через блок, имеющий форму диска, перекинут шнур. К концам шнура привязали грузы массой m₁= 100 г и m₂= 110 г. C каким ускорением а будут двигаться грузы, если масса m блока равна 400 г? Трение при вращении блока не учитывать.

1.39. Два тела массами m₁= 0,25 кг и m₂= 0,15 кг связаны тонкой нитью, перекинутой через блок. Блок закреплен на краю горизонтального стола, по поверхности которого скользит тело массой m. С каким ускорением двигаются тела и чему равны силы Т₁ и Т₂ натяжения нити по обе стороны от блока? Коэффициент трения тела о поверхность стола равен 0,2. Масса m блока равна 0,1 кг и ее можно считать равномерно распределенной по ободу. Массу нити и трение в подшипниках оси блока не учитывать.

1.40.Тело массой m₁= 0,25 кг, соединенное невесомой нитью при помощи блока с телом массой m₂= 0,2 кг, скользит по поверхности горизонтального стола. Масса блока m = 0,15 кг. Блок считать тонкостенным цилиндром. Коэффициент трения тела о поверхность равен 0,2. Не учитывая трение в подшипниках, найти: 1) ускорение, с которым будут двигаться тела; 2) силы натяжения Т₁ и Т₂ нити по обе стороны от блока.

1.41.Сплошной шар и цилиндр, имеющие одинаковый радиус, двигаются с одинаковой скоростью по горизонтальной плоскости, а затем поднимаются вверх по наклонной плоскости. Найти отношения высот подъема этих тел.

1.42.Колесо радиусом R = 30 см и массой m = 3 кг скатывается по наклонной плоскости длиной l = 5 м и углом наклона a= 25°. Найти момент инерции колеса, если его скорость v в конце движения равна 4,6 м/с.

1.43.Шар скатывается по наклонной плоскости с углом наклона 30°. Какую скорость будет иметь центр шара относительно наклонной плоскости через 1,5 с, если его начальная скорость была равна нулю?

1.44.Какой путь пройдет диск, катящийся без скольжения, вверх по наклонной плоскости с углом наклона 30°, если ему сообщена начальная скорость 7,0 м/с, параллельная наклонной плоскости?

1.45.К ободу однородного сплошного диска массой m = 10 кг, вращающемуся вокруг оси, приложена постоянная касательная сила

F = 30 Н. Найти кинетическую энергию диска через время t = 4 с после начала действия силы.

1.46.Тонкий прямой стержень длиной l = 1 м прикреплен к горизонтальной оси, проходящей через его конец. Стержень отклонили на угол y = 60° от положения равновесия и отпустили. Найти линейную скорость v нижнего конца стержня в момент прохождения через положение равновесия.

1.47.Маховик начинает вращаться из состояния покоя с постоянным угловым ускорением e = 0,4 с^-2. Найти кинетическую энергию маховика через время t = 25 с после начала движения, если через t₁= 10 с после начала движения момент импульса L₁ маховика составляет 60 кг^.м²/с.

1.48.Горизонтальная платформа массой m = 25 кг и радиусом
R = 0,8 м вращается с частотой n₁= 18 мин^-1. В центре стоит человек и держит в расставленных руках гири. Считая платформу диском, найти частоту вращения платформы, если человек опустит руки и уменьшит свой момент инерции от J₁ = 3,5 кг×м² до J₂ = 1 кг×м².

1.49.На горизонтальной платформе стоит человек и держит в руках стержень длиной l = 2,4 м и массой m = 8 кг, расположенный вертикально относительно оси вращения платформы? Платформа с человеком вращается с частотой n₁ = 1 с^-1. С какой частотой n₂ будет вращаться платформа с человеком, если он повернет стержень в горизонтальное положение? Сумма моментов инерции J человека и платформы равна 6 кг×м².

1.50.Платформа, имеющая форму сплошного однородного диска, может вращаться по инерции вокруг неподвижной вертикальной оси. На краю платформы стоит человек, масса которого в 3 раза меньше массы платформы. Найти, как и во сколько раз изменится угловая скорость вращения платформы, если человек перейдет ближе к центру на расстояние, равное половине радиуса платформы.

1.51.Определить мощность двигателя шахтной клети, поднимающего из шахты глубиной 200 м груз массой 1,0^.10⁴ кг за 60 с, если КПД равен 80%.

1.52.Найти работу, совершаемую при подъеме груза массой
m = 50 кг по наклонной плоскости с углом наклона a = 30° к горизонту на расстояние s = 4 м, если время подъема t = 2 с, а коэффициент трения m = 0,06.

1.53.Тело массой m = 0,4 кг скользит сначала по наклонной плоскости высотой h = 10 см и длиной l = 1 м, а затем по горизонтальной поверхности. Коэффициент трения на всем пути m = 0,04. Найти: 1) кинетическую энергию тела у основания плоскости; 2) путь, пройденный телом по горизонтальной поверхности до остановки.

1.54.Подвешенный на нити шарик массой m = 200 г отклоняют на угол a= 45°. Найти силу натяжения нити в момент прохождения шариком положения равновесия.

1.55.Груз массой m = 300 г подвешен на нити длиной l = 1 м. Нить отвели в сторону так, что она заняла горизонтальное положение, и отпустили. Найти силу натяжения нити в момент прохождения грузом положения равновесия.

1.56.Шарик массы m закреплен на конце жесткой спицы. Какую минимальную скорость в горизонтальном направлении необходимо сообщить шарику, чтобы он сделал полный оборот?

1.57.Шарик массы m висит на нити. Какую минимальную скорость в горизонтальном направлении необходимо сообщить шарику, чтобы он сделал полный оборот?

1.58.Небольшое тело начинает скользить с высоты h по наклонному желобу, который переходит в полуокружность радиусом
R = h/2. Пренебрегая трением, определить скорость тела в наивысшей точке его траектории (после отрыва от желоба).

1.59.Пренебрегая трением, определить наименьшую высоту h, с которой должна скатываться тележка с человеком по желобу, переходящему в петлю радиусом R = 6 м, и не оторваться от него в верхней точке петли.

1.60.Шарику, подвешенному на легкой нерастяжимой нити длиной l=1 м, толчком сообщили скорость v = 6 м/с. Найти высоту, на которой нить ослабнет и шарик перестанет двигаться по окружности. Чему равна скорость шарика в этот момент времени?

1.61.Какая энергия пошла на деформацию двух столкнувшихся шаров массами m₁ = m₂= 4,0 кг, если они двигались навстречу друг другу со скоростями v₁ = 3,0 м/с и v₂ = 8,0 м/с, а удар был прямой неупругий?

1.62.Тело массой m₁ = 3 кг двигается со скоростью v₁ = 2 м/с и ударяется о неподвижное тело такой же массы. Считая удар центральным и неупругим, найти количество теплоты, выделившееся при ударе.

1.63.Пуля массой m = 15 г, летящая горизонтально, попадает в баллистический маятник длиной l = 1 м и массой М = 1,5 кг и застревает в нем. Маятник в результате этого отклонился на угол j= 30°. Найти скорость пули.

1.64.Пуля массой m = 15 г, летящая горизонтально со скоростью v = 200 м/с, попадает в баллистический маятник длиной l = 1 м и массой М = 1,5 кг и застревает в нем. Найти угол отклонения j маятника.

1.65.На тонкой нити длиной 0,50 м подвешен пружинный пистолет так, что ствол размещен горизонтально. На какой угол отклонится нить после выстрела, если пуля массой m = 20 г при вылете со ствола имеет скорость v = 10 м/с? Масса пистолета М = 200 г.

1.66.Пуля массой m = 10 г, летящая со скоростью v = 600 м/с, попадает в баллистический маятник массой М = 5 кг и застревает в нем. На какую высоту h после удара поднялся маятник?

1.67.Пуля массой m = 15 г, летящая горизонтально, попадает в баллистический маятник длиной l = 1 м и массой М = 1,5 кг и застревает в нем. Маятник в результате этого отклонился на угол j= 30°. Найти скорость пули.

1.68.Пуля массой m = 15 г, летящая горизонтально со скоростью v = 200 м/с, попадает в баллистический маятник длиной l = 1 м и массой М = 1,5 кг и застревает в нем. Найти угол отклонения j маятника.

1.69.Два груза массами m₁= 10 кг и m₂= 15 кг подвешены на нитях длиной l = 2 м. Первоначально грузы соприкасаются между собой, затем меньший груз отклонили на угол j= 60° и отпустили. Найти высоту h, на которую поднимутся оба груза после удара. Удар грузов считать неупругим.

1.70.Два шара массами m₁= 0,20 кг и m₂= 0,80 кг подвешены на двух параллельных нитях длиной 2,0 м и соприкасаются между собой. Меньший шар отводится на 90° от первоначального положения и отпускается. Найти скорости шаров после столкновения, считая удар абсолютно неупругим? Какая часть энергии пойдет на нагревание шаров?

1.71.Два математических маятника, длины которых отличаются на Dl = 16 см, выполняют за одно и тоже время один n₁= 10 колебаний, другой – n₂ = 6 колебаний. Найти длины маятников l₁ и l ₂.

1.72.Шарик массой m = 200 г, подвешенный на пружине, колеблется с частотой n= 5,0 Гц. Найти коэффициент упругости пружины.

1.73.Стержень длиной l = 50 см выполняет колебания возле горизонтальной оси, которая проходит через точку, размещенную на расстоянии d = 12,5 см от конца стержня. Найти частоту колебаний стержня.

1.74.Однородный диск радиусом R = 20 см колеблется около горизонтальной оси, проходящей на расстоянии l = 15 см от центра диска. Определить период Т колебаний диска относительно этой оси.

1.75.Через сколько времени от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия на половину амплитуды? Период колебаний равен 24 с, начальная фаза равна нулю.

1.76.Начальная фаза гармонического колебания равна нулю. Через какую долю периода скорость точки будет равна половине его максимальной скорости?

1.77.Точка совершает гармонические колебания. Период колебаний 2 с, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда смещение точки от положения равновесия равно 25 мм.