Принцип адіабатної недосяжності. Ентропія. Математичне формулювання ІІ закону термодинаміки для рівноважних процесів

Другий закон термодинаміки

Принцип адіабатної недосяжності. Ентропія. Математичне формулювання ІІ закону термодинаміки для рівноважних процесів.

Розрахунок ентропії в процесах ідеального газу

ІІ закон термодинаміки для нерівноважних процесів. Закон зростання ентропії

Фізичний зміст ентропії

ІІІ закон термодинаміки

Література: [1] стор. 148-152,171-195, [2] стор. 271-297, [7] стор. 114-143

· Дайте статистичне тлумачення другого начала термодинаміки і вкажіть межі його застосування?

· Що таке ентропія і вільна енергія?

Принцип адіабатної недосяжності. Ентропія. Математичне формулювання ІІ закону термодинаміки для рівноважних процесів

Із ІІ закону термодинаміки випливає, що біля кожного рівноважного стану існують такі стани, в які не можна перейти рівноважним адіабатним шляхом (принцип адіабатної недосяжності Каратеодорі).

Справді, нехай із стану 1 система переходить в стан 2; при цьому система отримує певну кількість теплоти 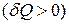і виконує роботу :

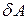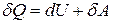. (1)

Припустимо, що із стану 2 система адиабатично переходить в стан 1, виконуючи роботу 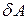, тоді

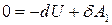. (2)

Додаючи (2) до (1), отримуємо, що за весь цикл була виконана робота 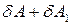, за рахунок некомпенсованого перетворення теплоти

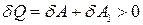. (3)

Оскільки за ІІ закон термодинаміки такий процес неможливий, то стан 1 адиабатично недосяжний із стану 2.

Отже ми повинні припустити, що з кожної рівноважної системи існує деяка функція стану, яка при рівноважних адіабатичних процесах не змінюється.

Тут можна розмірковувати наступним чином. Із того, що систему із деякого стану з температурою 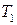не можна перевести ізотермічно (тобто коли розглядувана система знаходиться у тепловому контакті із тілом з дуже великою теплоємністю) в стан із температурою 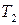, можна сформулювати закон ізотермічної недосяжності. В свою чергу, із принципу ізотермічної недосяжності можна було б вивести положення про існування у рівноважної системи температури. Аналогічно, якщо теплоізольовану (адіабатну) систему не можливо перевести із стану 1 в стан 2, то це означає, що деяка функція в положенні 1 має певне значення, яке відрізняється від її значення в положенні 2, а при адіабатичному рівноважному переході сама функція не змінюється.

Наша задача знайти цю функцію.

Пам’ятаємо, що повний приріст функції стану при круговому процесі дорівнює 0. Розглядаючи цикл Карно, ми отримаємо, що сума приведених теплот, що передається робочому тілу від нагрівача і віддається робочим тілом холодильнику, рівна нулю

.

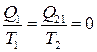Якщо ми зможемо показати, що інтеграл 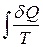не залежить від шляху для довільного випадку, ми одразу отримаємо вираз для нової функції стану.

Покажемо, що інтеграл 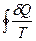не може бути додатною величиною.

Нехай система І в результаті деяких змін стану повертається у вихідний стан, тобто виконує круговий процес. Під час процесу система І поглинала і віддавала тепло. Уявимо собі, що тепло, яке виділяється системою, передається тепловому резервуару (тілу з великою теплоємністю), температура якого дорівнює 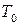. Цю передачу можна здійснити оборотним шляхом, наприклад з допомогою проміжного тіла, яке виконує цикл Карно, так що система І виконує роль нагрівача для проміжного тіла, а резервуар – роль холодильника.

Але для циклу Карно, кількість теплоти 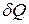, що віднімається від системи при температурі 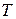, і кількість теплоти 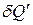, що передається резервуару при температурі 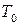не рівні одне одному, але рівні відношення 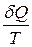і 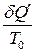. Звідси

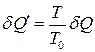. (4)

Якщо 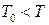, резервуар виконує роль холодильника, а система нагрівача. Якщо навпаки, 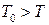, резервуар і система міняються ролями.

Після того система здійснила круговий процес, повна кількість теплоти, втрачена тілом, як це видно з (4),

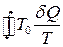. (5)

Але оскільки теплоємність теплового резервуару велика і його температура залишається незмінною, то

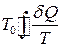. (6)

Процес, що здійснювався системою, - круговий. Тому система не зазнала змін. Проміжне тіло теж виконало круговий процес, а отже і в ньому не відбулись жодних змін.

Якщо б інтеграл 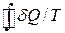виявились додатнім, то це означало б, що втрачена системою І кількість теплоти, рівна 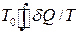, повністю перетворилась в роботу, в той час як ані система І, ані проміжне тіло не зазнали змін. Це протирічить принципу Томсона. Отже 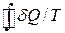не може бути більшим нуля.

Даний інтеграл не може бути і від’ємним. (Якщо 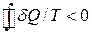, то при зворотному процеси ми отримаємо 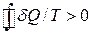, але, як показано, це неможливо.)

Якщо інтеграл не може бути ані додатнім, ані від’ємним, то це означає, що для рівноважних кругових процесів

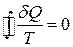. (7)

На основі цієї рівності вводиться фундаментальне поняття ентропії.

Із (7) випливає, що елементарна приведена теплота 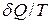є повним диференціалом деякої функції, яку позначимо буквою 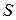і яка залежить тільки від стану термодинамічної системи. Приведена кількість теплоти, отримана системою при оборотному переході зі стану 1 у стан 2 (інтеграл 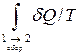) дорівнює різниці значень функції 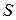в рівноважних станах 1 і 2

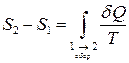. (8)

Вираз (8) дає математичне визначення термодинамічної ентропії.

З виразу (8) випливає, що термодинамічна ентропія, так само як і потенціальна енергія, визначається з точністю до довільної сталої. Тому формула (8) не дозволяє визначити абсолютне значення термодинамічної ентропії, а дає тільки різницю для двох рівноважних станів, як сумарну приведену теплоту в оборотному термодинамічному процесі, що переводить систему з одного стану в інший. На практиці необхідно знати не саму величину S, а тільки її зміну. Прийнято вважати, що S рівна нулеві при абсолютному нулеві.

Щоб визначити зміну ентропії у випадку необоротного переходу системи з одного стану в інший, потрібно придумати який-небудь оборотний процес, що зв'язує початковий і кінцевий стани, і знайти приведену теплоту, отриману системою при такому переході.

Вище ми відзначили, що диференціал ентропії визначається як

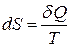. (9)

Формула (9) показує, що величина 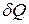, яка не є диференціалом, після ділення на 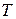стає повним диференціалом.

З (9) можна записати 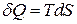. Для останнього виразу можна знайти аналогію з виразом для роботи 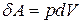. 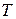- виступає в ролі термічно узагальненої сили, а 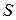- в якості узагальненої координати.

Нарешті (9) є математичним виразом для другого закону термодинаміки для рівноважних процесів. З допомогою (9) перший закон термодинаміки записується в формі

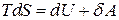(10)

- термодинамічна тотожність. Її також називають другим началом термодинаміки для рівноважних процесів.