Большой взрыв, черные дыры и эволюция вселенной 6 страница

Квантовая механика внесла неизбежный элемент непредсказуемости или случайности в науку. Эйнштейн настойчиво возражал против этого, несмотря на важную роль, которую он сам сыграл в развитии отрицаемых им идей. В действительности Эйнштейн получил Нобелевскую премию именно за вклад в создание квантовой теории. Однако он никогда не принял того, что Вселенной управляет случай; его чувства образно выражены в знаменитой фразе: «Бог не играет в кости».

Качество научной теории, как мы уже говорили, определяется ее способностью предсказывать результаты эксперимента. Квантовая теория ограничивает эту нашу способность. Не ограничивает ли квантовая теория возможности науки? Когда наука развивается, то пути ее движения должны диктоваться самой природой. В данном случае природа требует, чтобы мы пересмотрели то, что подразумеваем под предсказанием: мы не способны точно предсказать результат эксперимента, но можем многократно повторить эксперимент и подтвердить, что различные его исходы отмечаются с вероятностями, предсказанными квантовой теорией. Таким образом, принцип неопределенности не заставляет отказываться от веры в то, что миром управляют физические законы. На деле большинство ученых в конце концов приняли квантовую механику именно потому, что она великолепно согласуется с экспериментом.

Одно из наиболее важных следствий принципа неопределенности Гейзенберга заключается в том, что в некоторых отношениях частицы ведут себя подобно волнам. Как вы уже знаете, они не имеют определенного положения, но «размазаны» по пространству в соответствии с некоторым распределением вероятностей (рис. 24). Точно так же, хотя свет представляет собой волны, в некоторых отношениях он ведет себя так, будто состоит из частиц: свет может испускаться или поглощаться только определенными порциями, квантами. Фактически квантовая механика основана на совершенно новом математическом аппарате, который не описывает реальный мир ни в терминах частиц, ни в терминах волн. Для некоторых целей удобно рассматривать частицы как волны, для других — воспринимать волны как частицы, но подобный подход не более чем условность, принятая для нашего удобства. Это то, что физики называют корпускулярно‑волновым дуализмом квантовой механики.

Рис. 24. «Размазанное» квантовое положение.

Согласно квантовой теории невозможно ни определить с произвольно высокой точностью положение и скорость тела, ни точно предсказать ход будущих событий.

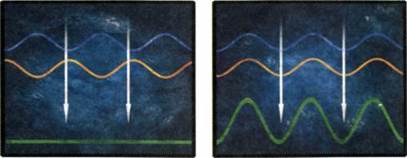
Важное следствие волнового квантово‑механического поведения — возможность наблюдать интерференцию между двумя наборами частиц. Об интерференции принято думать как о явлении волновой природы. При столкновении волн гребни одного их набора могут совпасть со впадинами другого набора (в этом случае говорят, что волны находятся «в противофазе»). Когда такое случается, два набора волн подавляют друг друга, а не образуют более сильную волну, как можно было бы ожидать (рис. 25). Самый знакомый всем пример интерференции света — радужная окраска мыльных пузырей. Она вызвана отражением света от внешней и внутренней поверхностей тонкой водяной стенки пузыря. Белый свет состоит из световых волн различной длины, а значит, разного цвета. Гребни волн определенной длины, отраженные от одной стороны водяной стенки, совпадают со впадинами волн, отраженных от другой стороны. Цвета, соответствующие этим длинам волн, отсутствуют в отраженном свете, который поэтому кажется окрашенным. Но квантовая теория говорит, что благодаря корпускулярно‑волновому дуализму интерференция может наблюдаться и у частиц.

Рис. 25. Волны, находящиеся в противофазе и совпадающие по фазе.

Если гребни и впадины двух волн совпадают, они образуют более сильную волну, но, если гребни одной волны совпадают со впадинами другой, они подавляют друг друга.

Самый известный пример — так называемый эксперимент с двумя щелями. Представьте себе перегородку (тонкую стенку), в которой имеется две узкие параллельные прорези. Прежде чем рассматривать, что случается при прохождении частиц через эти прорези, исследуем, что произойдет, когда на них падает свет. По одну сторону от преграды разместим световой источник строго определенного цвета (то есть с фиксированной длиной волны). Б о льшая часть испущенного света попадет на перегородку, но некоторое количество пройдет через щели. Теперь допустим, что по другую сторону загородки установлен экран.

Рассмотрим любую точку на этом экране. Ее достигнут волны, проникшие через обе прорези. Однако в общем случае свет, прошедший через одну щель, на пути от источника к нашей точке покроет иное расстояние, нежели свет, прошедший через другую щель. Из‑за этого различия расстояний волны, пришедшие к точке от двух разных щелей, не совпадут по фазе (рис. 26). В некоторых местах впадины одной волны совпадут с гребнями другой и эти волны погасят друг друга; в других гребни совпадут с гребнями, а впадины — со впадинами и волны взаимно усилятся; но в большинстве точек будет наблюдаться некое промежуточное состояние. Результат — характерное чередование светлых и темных полос.

Рис. 26. Пути световых волн и интерференция.

В эксперименте с двумя щелями расстояние, которое покроет свет, прошедший через верхнюю и нижнюю щели, различно для разных точек экрана. В итоге волны взаимно усиливаются на одних участках и гасят друг друга на других, формируя интерференционную картину из темных и светлых полос.

Замечательный факт состоит в том, что та же самая картина отмечается, если источник света заменить источником, испускающим частицы, например электроны, обладающие одинаковой скоростью (а значит, соответствующие волны материи имеют одинаковую длину). Предположим, что вы бомбардируете электронами стенку с одной щелью. Большинство электронов будет остановлено стеной, но некоторые пройдут сквозь щель и доберутся до экрана, расположенного с другой стороны. Поэтому напрашивается вывод, что открытие в перегородке второй щели лишь увеличит число электронов, попадающих в каждую точку экрана. Однако когда вы открываете вторую щель, то число электронов, попадающих на экран, в некоторых точках увеличивается, а в других — уменьшается, как будто электроны испытывают интерференцию, подобно волнам, а не ведут себя как частицы (рис. 27).

Рис. 27. Распределение электронов.

Вследствие интерференции одновременная бомбардировка электронами двух щелей дает иной результат, нежели бомбардировка каждой из них в отдельности.

Теперь представим себе, что мы посылаем электроны сквозь щель по одному за раз. Сохранится ли в этом случае интерференция? Можно было бы ожидать, что каждый электрон будет проходить через одну из двух щелей и в результате интерференционный узор исчезнет. В действительности, однако, даже при бомбардировке щелей одиночными электронами интерференция по‑прежнему наблюдается. Значит, каждый электрон должен одновременно проходить через обе щели и интерферировать сам с собой! Явление интерференции частиц имело принципиальное значение для понимания строения атомов, основных элементов, из которых состоим мы сами и все вокруг нас. В начале двадцатого столетия считалось, что, подобно тому как планеты обращаются вокруг Солнца, и электроны (отрицательно заряженные частицы) в атомах обращаются вокруг ядра, несущего положительный заряд. Предполагалось, что притяжение между положительным и отрицательным электрическими зарядами удерживает электроны на орбитах, подобно тому как притяжение Солнца не дает планетам сойти с их орбит. Одна беда: классические законы механики и электричества — до квантовой механики — предсказывали, что электроны, обращающиеся подобным образом, должны испускать излучение. Будь это так, они неизбежно теряли бы энергию и двигались по спирали к ядру до столкновения с ним. Следовательно, атомы — и вообще вся материя — должны были бы стремительно сколлапсировать в состояние с чрезвычайно высокой плотностью, чего явно не происходит!

Датский ученый Нильс Бор частично разрешил эту проблему в 1913 г . Он предположил, что электроны, возможно, способны обращаться не на любом расстоянии от ядра, но только на некоторых специфических расстояниях. Если также допустить, что только один или два электрона могут обращаться вокруг ядра на каждом из этих фиксированных расстояний, то проблема коллапса решается, потому что после заполнения ограниченного числа внутренних орбит движение электронов по спирали к ядру прекращается. Данная модель убедительно объяснила структуру самого простого атома — атома водорода, в котором вокруг ядра обращается один‑единственный электрон. Но оставалось неясным, как распространить эту модель на более сложные атомы. Кроме того, идея относительно ограниченного набора разрешенных орбит выглядела искусственным временным приемом. Эта уловка работала математически, но она не объясняла, почему физические процессы протекают так, а не иначе, и какой фундаментальный закон — если таковой существует — за этим стоит. Новая теория — квантовая механика — позволила преодолеть эти затруднения. Она показала, что электрон, обращающийся вокруг ядра, можно рассматривать как волну, длина которой зависит от скорости ее распространения. Представьте себе волну, обегающую ядро на определенном расстоянии, как постулировал Бор. Длина окружности некоторых орбит будет соответствовать целому (не дробному) числу длин волны электрона. На таких орбитах гребни волн при каждом витке окажутся в одних и тех же положениях, так что волны будут складываться друг с другом. Эти орбиты соответствуют разрешенным орбитам Бора. В то же время на орбитах, где не укладывается целое число длин волн, гребни будут накладываться на впадины, приводя к затуханию волн. Это запрещенные орбиты. Таким образом, закон Бора о разрешенных и запрещенных орбитах получил объяснение (рис. 28).

Рис. 28. Волны на атомных орбитах.

Нильс Бор полагал, что в атоме электронные волны бесконечно обегают ядро. Согласно его модели только те орбиты, длина окружности которых соответствует целому числу длин волн электрона, не испытывают разрушительной интерференции.

Удачным примером наглядного представления корпускулярно‑волнового дуализма являются так называемые интегралы по траекториям, предложенные американским ученым Ричардом Фейнманом. Этот подход, в отличие от классического, неквантового, не предполагает, что у частицы имеется некая единственная история или, иными словами, траектория в пространстве‑времени. Вместо этого считается, что частица движется из точки А в точку В по всем возможным траекториям (рис. 29). С каждой траекторией между А и В Фейнман связал пару чисел. Одно из них представляет амплитуду, или размах, волны. Другое — фазу, то есть положение в цикле колебания (гребень или впадина). Вероятность того, что частица попадет из А в В, определяется сложением волн для всех траекторий, соединяющих А и В. Как правило, если сравнить набор соседних траекторий, то фазы, то есть положения в цикле колебаний, будут очень сильно различаться. Значит, волны, следующие данными траекториями, почти в точности погасят друг друга. Однако у некоторых наборов соседних траекторий различие фаз не столь значительно. Волны, распространяющиеся по таким траекториям, не будут гаситься. Подобные траектории соответствуют разрешенным орбитам Бора.

Рис. 29. Множество траекторий электрона в эксперименте с двумя щелями.

Согласно квантовой теории в формулировке Ричарда Фейнмана частица, подобная этой, летящей от источника к экрану, движется по всем возможным траекториям сразу.

Воплощение изложенных идей в конкретной математической форме позволило относительно легко вычислять разрешенные орбиты в сложных атомах и даже в молекулах, которые состоят из множества атомов, связанных электронами, чьи орбиты охватывают сразу несколько ядер. И поскольку строение молекул и их взаимодействие составляют основу химии и биологии, квантовая механика позволяет нам в принципе предсказывать почти все, что мы видим вокруг, в пределах ограничений, установленных принципом неопределенности. (На практике, однако, мы не можем решить уравнения ни для какого атома, кроме самого простого, атома водорода, в котором только один электрон, и пользуемся приближениями и компьютерами для анализа более сложных атомов и молекул.)

Квантовая теория оказалась невероятно успешной и легла в основу почти всей современной науки и техники. Она управляет поведением транзисторов и интегральных схем — важнейших компонентов электронных устройств, таких как телевизоры и компьютеры, и составляет фундамент современной химии и биологии. Единственная область физической науки, в которую квантовая механика пока еще не проникла, — это гравитация и крупномасштабная структура Вселенной. Общая теория относительности Эйнштейна не принимает во внимание квантовомеханический принцип неопределенности, что необходимо для согласования с другими теориями.

Как уже было показано в предыдущей главе, общая теория относительности требует видоизменения. Предсказав существование точек с бесконечной плотностью — сингулярностей, — классическая (то есть не квантовая) общая теория относительности тем самым предрекла собственное крушение, подобно тому как классическая механика предопределила свой крах, предсказав, что абсолютно черные тела должны излучать бесконечную энергию, а атомы — коллапсировать, достигая бесконечной плотности. И, как и в случае с классической механикой, мы надеемся устранить эти неприемлемые сингулярности, превратив классическую общую теорию относительности в квантовую теорию, то есть создав квантовую теорию гравитации.

Если общая теория относительности неверна, почему же все эксперименты до настоящего времени подтверждают ее? Причина того, что мы до сих пор не заметили никаких расхождений между теорией и наблюдениями, состоит в том, что все гравитационные поля, с которыми нам обычно приходится сталкиваться, очень слабые. Но, как мы уже говорили, в зарождающейся Вселенной, где все вещество и энергия сосредоточены в ничтожно малом объеме, гравитационное поле должно быть очень сильным. В присутствии столь сильных полей эффекты квантовой теории должны быть весьма существенны.

Хотя квантовая теория гравитации еще не создана, мы знаем множество свойств, которыми, как нам думается, она должна обладать. Во‑первых, она должна включать в себя фейнмановскую схему, представляющую квантовую теорию в терминах интегралов по траекториям. Во‑вторых, частью любой окончательной теории, по нашему убеждению, должна быть идея Эйнштейна о представлении гравитационного поля как искривления пространства‑времени: в искривленном пространстве частицы стремятся следовать по пути, наиболее приближенному к прямой линии, но поскольку пространство‑время не является плоским, их траектории выглядят изогнутыми, как если бы на них действовало гравитационное поле. Когда мы применяем фейнмановские интегралы по траекториям к взглядам Эйнштейна на гравитацию, аналогом траектории частицы становится полностью все искривленное пространство‑время, представляющее историю всей Вселенной.

Классическая теория гравитации предусматривает только два возможных сценария поведения Вселенной: либо она существовала всегда, на протяжении бесконечного времени, либо ведет свое начало от сингулярности, которая имела место в прошлом, некоторое конечное время назад. По причинам, обсуждавшимся выше, мы полагаем, что Вселенная не существовала всегда. Но если она имела начало, то согласно классической общей теории относительности, чтобы узнать, какое именно решение уравнений Эйнштейна описывает нашу Вселенную, нам нужно знать ее начальное состояние, то есть точное состояние, с которого началось ее развитие. Быть может, Бог и установил изначально законы природы, но, кажется, с тех пор Он предоставил Вселенной развиться в согласии с ними без Его вмешательства. Как Он выбирал начальное состояние или конфигурацию Вселенной? Каковы были «граничные условия» в начале времен? Этот вопрос вызывает затруднения в классической общей теории относительности, потому что она неприменима к моменту зарождения Вселенной.

С другой стороны, квантовая теория гравитации открывает новые возможности для разрешения указанной проблемы. В квантовой теории пространство‑время может быть конечным по протяженности и в то же время не иметь сингулярностей, формирующих границу или край. Такое пространство‑время походило бы на поверхность Земли, только с двумя дополнительными измерениями. Как уже отмечалось, путешествуя в некотором направлении по поверхности Земли, никогда не встречаешь непреодолимого барьера или края и в конечном счете возвращаешься туда, где начал путь, не рискуя сверзиться с края света или пропасть в сингулярности. Так что, если бы нам посчастливилось создать квантовую теорию гравитации, она позволила бы нам избавиться от сингулярностей, где перестают работать законы природы.

Коль скоро пространство‑время не имеет никаких границ, то ни к чему выяснять, как оно ведет себя на границе, — нет нужды знать начальное состояние Вселенной. Не существует края пространства‑времени, вынуждающего нас обращаться к идее Бога или искать некоторый новый закон, чтобы установить граничное состояние пространства‑времени. Это можно выразить так: граничное состояние Вселенной состоит в том, что она не имеет никаких границ. Такая Вселенная будет полностью обособленной, не взаимодействующей ни с чем вне себя. Ее нельзя ни создать, ни разрушить. Она просто есть. Пока мы полагали, что Вселенная имеет начало, роль Создателя казалась ясной. Но если Вселенная действительно полностью автономна, не имеет ни границ, ни краев, ни начала, ни конца, то ответ на вопрос о роли Создателя перестает быть очевидным.

Глава десятая