Циклотронный резонанс. Циклотронная масса.
 Рис.5.4. Пояснение к выводу соотношения (5.9) Рис.5.4. Пояснение к выводу соотношения (5.9) |
Метод циклотронного резонанса, так же как и метод аномального скин-эффекта, основан на исследовании затухания микроволнового поля при проникновении его в металл. Строго говоря, в эксперименте здесь определяется не геометрия поверхности Ферми, а "циклотронная масса", пропорциональная энергетическому градиенту площади поперечного сечения поверхности Ферми ∂S/  E.
E.
Рассмотрим орбиту блоховского электрона с энергией Е в постоянном магнитном поле, лежащую в какой-либо плоскости, перпендикулярной магнитному полю, рис. 5.4. Для прохождения части орбиты в k-пространстве между значениями k1 и k2 требуется время
 t = t2 - t1 =
t = t2 - t1 =  =
=  =
= 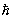 2c/(eB)
2c/(eB) 
Градиент dE/dk ~ 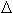 E/
E/  k, где
k, где 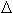 k направлено
k направлено 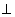 -но траектории (градиент dE/dk перпендикулярен изоэнергетической поверхности!), в отличие от dk, которое направлено вдоль нее. Т.е.
-но траектории (градиент dE/dk перпендикулярен изоэнергетической поверхности!), в отличие от dk, которое направлено вдоль нее. Т.е.
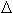 t
t 
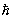 2c/(eB
2c/(eB 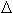 E)
E)  kdk = (
kdk = ( 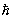 2c/eB)(
2c/eB)( 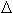 S1,2/
S1,2/ 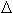 E).
E).
При 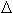 E
E  0 получаем для замкнутой траектории период движения:
0 получаем для замкнутой траектории период движения:
T = ( 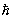 2c/eB)[∂S(E,kz)/∂E] 2c/eB)[∂S(E,kz)/∂E] | (5.9) |
Для свободных электронов:
T = 2 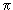 / / 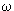 c = (2 c = (2 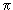 mc/ eB) mc/ eB) | (5.10а) |
Это же выражение может быть использовано для блоховских электронов:
T = (2 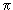 m*c/ eB), m*c/ eB), | (5.10б) |
где
m* = ( 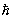 2/2 2/2 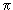 )[ )[  S(E,kz)/ S(E,kz)/  E] E] | (5.11) |
- эффективная циклотронная масса электрона.
В описанном методе условие резонанса достигается в микроволновом диапазоне. При этих частотах имеет место аномальный режим поглощения, когда толщина скин-слоя становится часто меньше длины свободного пробега электронов и меньше размеров орбиты (в r-пространстве).
Эффект Азбеля-Канера.
 Рис.5.5. Эффект Азбеля-Канера Рис.5.5. Эффект Азбеля-Канера |
Азбель М.Я. и Канер Э.А. (ЖЭТФ, 32 (1956) 896) предложили направить магнитное поле параллельно поверхности, что приводит к геометрии эксперимента, изображенной на рис. 5.5. Если ощущаемое электроном электрическое поле имеет одну и ту же фразу при каждом его проходе через скин-слой, то электрон может резонансно поглощать энергию поля. При этом период обращения электрона, Т, должен быть кратен периоду колебаний электрического поля, ТЕ. С учетом (5.10) и (5.11) имеем T = nTE, и
1/B = n(2 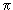 / / 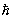 2c 2c 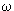 )(1/[ )(1/[  S(E,kz)/ S(E,kz)/  E]) E]) | (5.12) |
где 2 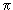 /
/ 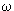
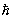 TE.
TE.
Из условия резонанса (5.12) следует, что если изобразить поглощение энергии микроволнового поля как функцию от 1/В, то резонансные пики, отвечающие отдельному циклотронному периоду, будут располагаться через равные промежутки. Отсюда получаем  S(E,kz)/
S(E,kz)/  E. Проблема метода состоит в том, что несколько циклотронных масс могут давать вклад, что усложняет картину осцилляций.
E. Проблема метода состоит в том, что несколько циклотронных масс могут давать вклад, что усложняет картину осцилляций.
Эффект Гантмахера (Гантмахер В.Ф., ЖЭТФ, 43 (1962) с.345)
 Рис. 5.6. Эффект Гантмахера Рис. 5.6. Эффект Гантмахера |
Эффект Гантмахера состоит в резонансном возрастании интенсивности проходящего через тонкую металлическую пластину УВЧ-излучения (мегагерцовый диапазон) в параллельном поверхности пластины постоянном магнитном поле. Если толщина образца h больше толщины скин-слоя, но меньше длины свободного пробега электронов, l :  0 < h < l, то электрическое поле будет действовать на электроны, находящиеся в пределах скин-слоя. Так же, электроны могут вызвать излучение энергии только если они находятся в пределах ских-слоя у поверхности.
0 < h < l, то электрическое поле будет действовать на электроны, находящиеся в пределах скин-слоя. Так же, электроны могут вызвать излучение энергии только если они находятся в пределах ских-слоя у поверхности.
При условии  0 < h < l в магнитном поле, возможны орбиты электронов, простирающиеся от скин-слоя от передней до задней поверхностей пластинки. Такие орбиты способны производить на задней поверхности электрический ток, который вызван приложенным снаружи электрическим УВЧ-полем на ее передней поверхности. Это приводит к генерации электромагнитного излучения с задней стороны пластинки. Поэтому в тех случаях, когда толщина h и величина магнитного поля В согласованы, должно наблюдаться резонансное возрастание прохождения электромагнитного излучения через пластинку. Как и в других методах эффективными оказываются электроны вблизи поверхности Ферми и с орбитами с экстремальными линейными размерами.
0 < h < l в магнитном поле, возможны орбиты электронов, простирающиеся от скин-слоя от передней до задней поверхностей пластинки. Такие орбиты способны производить на задней поверхности электрический ток, который вызван приложенным снаружи электрическим УВЧ-полем на ее передней поверхности. Это приводит к генерации электромагнитного излучения с задней стороны пластинки. Поэтому в тех случаях, когда толщина h и величина магнитного поля В согласованы, должно наблюдаться резонансное возрастание прохождения электромагнитного излучения через пластинку. Как и в других методах эффективными оказываются электроны вблизи поверхности Ферми и с орбитами с экстремальными линейными размерами.
