Все, что может случиться, действительно случается

Итак, теперь можно заняться детальным исследованием квантовой теории. Техническое содержание основных идей довольно простое – сложно лишь примириться с тем, что они бросают вызов нашим предубеждениям по поводу устройства мира. Мы уже говорили, например, что частицу можно представить в виде множества маленьких циферблатов, расставленных здесь и там, и что длина стрелки такого циферблата (возведенная в квадрат) соответствует вероятности, с которой частицу можно обнаружить в конкретном месте. Циферблаты – это не суть системы, а математический инструмент, которым мы пользуемся, чтобы вычислить шансы найти где‑то нашу частицу. Мы привели правило сложения циферблатов, необходимое для описания феномена интерференции. Сейчас нам нужно окончательно свести концы с концами и сформулировать правило, которое объясняло бы, как циферблаты изменяются от одного момента к другому. Это правило послужит заменой первому закону Ньютона в том смысле, что позволит спрогнозировать действия частицы, оставленной в покое. Сначала представим одиночную частицу в некоторой точке.

Мы знаем, как представлять частицу в точке (рис. 4.1). Итак, изображен одиночный циферблат с длиной стрелки 1 (потому что 1 в квадрате – это и есть 1, стало быть, вероятность найти частицу в этой точке равна 1, то есть 100 %). Предположим, что на циферблате 12 часов, хотя этот выбор совершенно произволен. С точки зрения вероятности стрелка часов может указывать в любом направлении, но надо же с чего‑то начать, так что условимся на 12 часов. Мы хотим добиться ответа на следующий вопрос: каковы шансы того, что частица позже будет находиться где‑то еще? Иными словами, сколько еще циферблатов нужно нарисовать и где их поместить в следующее мгновение? Исааку Ньютону на такой очевидный вопрос отвечать было бы даже скучно: если мы размещаем где‑то частицу и ничего с ней не делаем, она никуда и не движется. Но природа весьма категорично утверждает, что это попросту неверно. На самом деле Ньютон не мог ошибиться еще сильнее.

Рис. 4.1. Одиночный циферблат, представляющий частицу, которая четко локализуется в конкретной точке пространства

А вот и правильный ответ: частица в следующий момент может оказаться в любой точке Вселенной . Это значит, что нам придется нарисовать бесконечное множество циферблатов – по одному для каждой мыслимой точки в пространстве. Это предложение стоит перечитать много раз. Наверное, лучше раскрыть эту мысль.

Допущение, что частица может быть где угодно, эквивалентно полному отсутствию предположений по поводу ее движения. Это самое беспристрастное допущение, которое мы можем сделать, и такое решение обладает определенной аскетической[7]привлекательностью, хотя, по общему признанию, действительно кажется, что оно нарушает все законы здравого смысла, а заодно, возможно, и законы физики.

Циферблат представляет нечто определенное – вероятность того, что частица будет обнаружена на месте этого циферблата. Если мы знаем, что частица находится в конкретном месте в конкретное время, то представляем это в виде одиночного циферблата в этой точке. Но если мы начнем с частицы, находящейся в нулевой момент времени в определенном месте, то для «нулевого момента плюс еще сколько‑то времени» придется нарисовать огромное – на самом деле бесконечное – количество других циферблатов, заполняющих всю Вселенную. Так подтверждается возможность того, что частица перепрыгивает в любое другое место в одно мгновение. Наша частица будет одновременно и в нанометре от исходного положения, и в миллиарде световых лет отсюда, в ядре звезды отдаленной галактики. Звучит, говоря по‑простому, странно. Но нужно со всей ясностью сказать: теория должна быть способна объяснить двухщелевой эксперимент, и как волна начинает распространяться, если обмакнуть в стоячую воду палец ноги, так и электрон, изначально расположенный в некой точке, должен распространяться с течением времени. Нужно только установить, как именно он распространяется.

Мы предполагаем, что, в отличие от водяной волны, электронная волна распространяется по всей Вселенной мгновенно. В техническом смысле можно сказать, что правило распространения частиц отличается от правила распространения водяной волны, хотя в обоих случаях распространение соответствует «волновому уравнению». Уравнение для водяных волн отличается от уравнения волн‑частиц (это то самое знаменитое уравнение Шрёдингера, которое мы упомянули в прошлой главе), но оба они связаны с физикой волн. Различия – в деталях того, как объекты движутся с места на место. Кстати, если вы немного в курсе теории относительности Эйнштейна, то должны бы занервничать, услышав, что мы ведем речь о мгновенных перемещениях частицы по Вселенной, так как получается, словно что‑то передвигается быстрее скорости света. На самом же деле идея того, что частица может быть здесь и через мгновение очень далеко отсюда, сама по себе вовсе не противоречит теориям Эйнштейна, потому что суть их в том, что быстрее скорости света не может перемещаться информация , а этому ограничению квантовая теория удовлетворяет. Как мы вскоре увидим, динамика прыжков частиц через Вселенную совершенно не такая, как при передаче информации, потому что мы не можем сказать заранее, куда же прыгнет частица. Кажется, что наша теория строится на полной анархии, и будет вполне естественно, если вы не поверите, что природа так себя может вести. Но далее в этой книге мы убедимся, что порядок нашей повседневной жизни действительно берет свое начало в этом фантастически абсурдном поведении.

Если вам непросто переварить подобную анархию – например, необходимость наполнить всю Вселенную маленькими циферблатами, чтобы описать движение единственной субатомной частицы от одного момента к другому, – то вы в хорошей компании. Снятие покровов с квантовой теории и попытки истолковать ее внутреннюю деятельность поставят в тупик кого угодно. Нильс Бор, например, известен такой фразой: «Те, кто не пришел в ужас при знакомстве с квантовой механикой, просто не могут ее понять». Ричард Фейнман предварил третий том «Фейнмановских лекций по физике» словами: «Думаю, могу с уверенностью сказать, что никто не понимает квантовую механику». К счастью, следовать ее законам гораздо проще, чем пытаться разобраться в ее сути. Способность тщательно рассматривать последствия определенного набора предположений, не слишком затрудняя себя их философским смыслом, – одно из самых важных умений современного физика. Это как раз в духе Гейзенберга: зададим первичные предположения и вычислим их последствия. Если мы получаем набор предсказаний, согласующихся с повседневными наблюдениями, теория признается жизнеспособной.

Многие проблемы слишком сложны, чтобы решить их одним мыслительным усилием, а глубокое понимание редко приходит в моменты, когда ученый кричит «эврика». Нужно убедиться, что вы действительно понимаете каждый мельчайший шаг, и после достаточного количества шагов должно появиться понимание общей картины. В противном случае мы поймем, что пошли по ложному пути и нужно начинать все с начала. Эти мельчайшие шаги, которые мы упомянули, не так сложны, но идея взять один циферблат и превратить его в бесконечное множество циферблатов, безусловно, сложна, особенно если представить себе, что их все надо нарисовать. Вечность, если перефразировать Вуди Аллена, – это очень долго, особенно ближе к концу. Советуем не паниковать и не сдаваться. В любом случае мы имеем дело лишь с кусочком вечности. Наша следующая задача – установить правило, которое будет описывать поведение этих циферблатов в определенное время после запуска частицы.

Это правило – основной закон квантовой теории, хотя впоследствии нам понадобится и второй закон, когда мы перейдем к рассмотрению возможности наличия во Вселенной больше одной частицы. Но начнем по порядку и сначала сосредоточимся на единственной на всю Вселенную частице: никто не обвинит нас в том, что мы хватаемся за все сразу. Итак, она существует в один миг времени – предположим, мы точно знаем, в какой именно, – и представлена единственным циферблатом. Наша конкретная задача – найти правило, описывающее, как будут выглядеть в любой момент все новые циферблаты, рассеянные по Вселенной.

Сначала мы сформулируем это правило, не подводя под него никаких оснований. К тому, почему правило звучит именно так, а не иначе, вернемся через несколько абзацев, но сейчас должны просто принять его на веру. Итак, вот оно: во время t в будущем стрелка циферблата, находящегося на расстоянии x от исходного циферблата, продвинется против часовой стрелки на величину, пропорциональную x ²; величина продвижения также пропорциональна массе частицы m и обратно пропорциональна времени t. В записи с помощью символов это значит, что нам нужно повернуть стрелку против хода часов на величину, пропорциональную mx ² / t . А если объяснять это словами, то быстрее двигаются по циферблату более массивные частицы, более далекие от исходной точки, а с течением времени ход становится медленнее. Существует алгоритм – или, если угодно, рецепт, – который точно описывает, как определить поведение определенного набора циферблатов в какой‑то момент будущего. В каждой точке Вселенной мы рисуем новый циферблат, стрелка которого сдвинута на заданную правилом величину. Это подкрепляет наше предположение о том, что частица может (и так оно и есть) перепрыгивать из начального положения в любую другую точку Вселенной, порождая в процессе движения новые циферблаты.

Для простоты мы представляли только один исходный циферблат, но, конечно, в какой‑то момент времени уже может существовать несколько циферблатов, и это отражает постулат, что частица не находится в каком‑то определенном месте. Как разобраться с целой кучей циферблатов? Ответ таков: нужно делать то, что мы делали для одного циферблата, и повторять процесс для всех имеющихся циферблатов. Эту идею иллюстрирует рис. 4.2. Первичный набор циферблатов представлен маленькими кружками, а стрелки показывают, как частица перепрыгивает с места каждого первичного циферблата в точку X , «оставляя» там новый циферблат. Конечно, при этом каждый первичный циферблат порождает в точке X новый циферблат, и мы должны сложить их все вместе, чтобы создать окончательный циферблат для точки X . Размер этого окончательного циферблата дает вероятность впоследствии найти частицу в точке X .

.

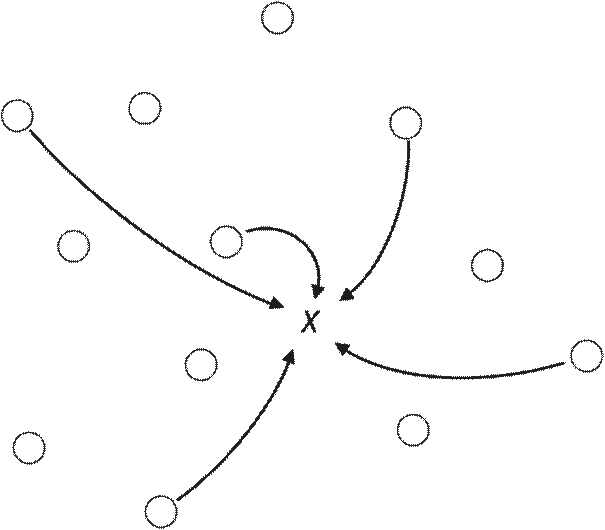
Рис. 4.2. Прыгающие циферблаты. Окружности соответствуют местонахождению частицы в определенный момент времени; нам необходимо каждой такой точке поставить в соответствие по циферблату. Чтобы вычислить вероятность обнаружения частицы в точке X , мы должны позволить частице прыгнуть туда из всех исходных мест ее пребывания. Несколько таких прыжков обозначено стрелками. Форма линий не имеет никакого значения и уж точно не означает, что частица движется с места нахождения циферблата в точку X по какой‑то определенной траектории

Необходимость сложения всех появляющихся в точке циферблатов не так уж странна. Каждый циферблат соответствует специфической траектории, по которой частица могла бы прибыть в точку X . Сложение циферблатов легко понять, если вернуться к двухщелевому эксперименту: мы просто пытаемся перефразировать описание волны для циферблатов. Можем представить два исходных циферблата – по одному у каждой щели. Каждый из них порождает новый циферблат на конкретной точке экрана в одно из последующих мгновений, и мы должны сложить эти два циферблата, чтобы получилась интерференционная фигура[8]. Итак, правило предсказания внешнего вида циферблата в любой точке состоит в том, чтобы перенести в эту точку все исходные циферблаты, один за другим, а потом сложить их все по правилу сложения, описанному в предыдущей главе.

Так как мы решили описывать подобным языком распространение волн, можно использовать его и при размышлениях о более знакомых нам волнах. Самой идее уже много лет. Известно, что голландский физик Христиан Гюйгенс описывал так световые волны еще в 1690 году. Он, конечно, не упоминал воображаемых циферблатов, скорее подчеркивал, что каждую точку световой волны нужно рассматривать в качестве источника вторичных волн (как каждый циферблат порождает множество новых). Эти вторичные волны затем соединяются, что дает новую волну. Процесс повторяется, так что каждая точка новой волны служит источником результирующих волн, которые вновь соединяются друг с другом, и таким способом волна продвигается дальше.

Теперь можно вернуться к тому моменту, который может вызывать ваше справедливое беспокойство. Почему мы выбрали величину mx ² / t для определения сдвига часовой стрелки? У этой величины есть имя – это действие – и долгая почтенная история в развитии физики. На самом деле никто пока не понимает, почему эта величина настолько прочно укоренилась в природе, а стало быть, никто не может рационально объяснить, почему стрелки движутся так, как движутся. Возникает вопрос: как вообще кто‑то понял, что это так важно? Понятие действия впервые предложил немецкий философ и математик Готфрид Лейбниц в написанной в 1669 году, но неопубликованной работе, однако он не сумел найти способ производить вычисления с его помощью. Вновь ввел его в 1744 году французский ученый Пьер Луи де Мопертюи, а затем его использовал для формулировки нового и очень мощного принципа природы друг Мопертюи, математик Леонард Эйлер. Представьте себе мяч, летящий по воздуху. Эйлер обнаружил: мяч движется по такой траектории, что действие между двумя точками маршрута будет каждый раз наименьшим. В случае с мячом действие соотносимо с разностью между кинетической и потенциальной энергией мяча[9]. Эта закономерность получила название «принципа наименьшего действия», и он может быть использован как альтернатива ньютоновым законам движения. На первый взгляд, принцип довольно странен, потому что кажется, будто для полета с наименьшим действием шар должен заранее знать, куда он собирается лететь еще до того, как он туда полетит. Как иначе он мог бы лететь по воздуху так, чтобы величина, именуемая действием, каждый раз получалась минимальной, когда он уже пролетел? Если перефразировать, то принцип наименьшего действия кажется телеологическим (так говорят, когда предполагают, что события происходят с целью достичь заранее предопределенного исхода). Телеологические идеи вообще пользуются в науке дурной репутацией, и несложно догадаться почему. В биологии телеологическое объяснение появления сложных существ подкрепляло бы теорию существования творца, в то время как теория эволюции путем естественного отбора, выдвинутая Дарвином, предлагает гораздо более простое объяснение, которое к тому же прекрасно согласуется с имеющимися данными. В теории Дарвина нет телеологического компонента: случайные мутации ведут к появлению вариаций в организмах, а внешнее давление со стороны среды и других живых существ определяет, какие вариации передаются следующим поколениям. Этот процесс – единственный, способный объяснить то многообразие и сложность жизненных форм, которые мы наблюдаем сейчас на Земле. Иными словами, устраняется необходимость божественного промысла и постепенного восхождения организмов к какому‑то совершенству. Вместо этого оказывается, что эволюция жизни – случайный путь, который определяется несовершенным копированием генов в постоянно меняющихся условиях внешней среды. Лауреат Нобелевской премии французский биолог Жак Моно даже назвал краеугольным камнем современной биологии «систематическое или аксиоматическое отрицание возможности того, что научное знание может быть получено на основе теорий, которые явным или неявным образом включают в себя телеологический принцип».

У физиков, однако, споры о том, работает ли принцип наименьшего действия, не ведутся, потому что он позволяет производить вычисления, верно описывающие природу, и является краеугольным камнем физики. Можно возразить, что принцип наименьшего действия вовсе не телеологический, но все споры в любом случае закончатся, когда мы возьмем на вооружение подход Фейнмана к квантовой механике. Мяч, летящий по воздуху, «знает», какую траекторию избрать, потому что на самом деле втайне исследует каждую возможную траекторию.

Как же выяснилось, что правило хода стрелок часов имеет нечто общее с величиной, именуемой действием? В исторической перспективе первым такую формулировку квантовой теории, включающей понятие действия, предложил Дирак, но со свойственной ему эксцентричностью опубликовал свое исследование в советском журнале – в знак поддержки советской науки. Статья под названием «Лагранжиан в квантовой механике» была опубликована в 1933 году и пребывала в забвении много лет. Весной 1941 года молодой Ричард Фейнман размышлял, как разработать новый подход к квантовой теории, используя лагранжеву формулировку классической механики (эта формулировка вытекает из принципа наименьшего действия). Однажды вечером на пивной вечеринке в Принстоне он встретил Герберта Йеле, европейского физика, и, как это водится у физиков, после нескольких кружек они начали обсуждать идеи для исследований. Йеле вспомнил давнюю статью Дирака, и на следующий день они нашли ее в Принстонской библиотеке. Фейнман немедленно начал вычисления по методам Дирака, и в течение дня на глазах у Йеле обнаружил, что может вывести уравнение Шрёдингера из принципа наименьшего действия. Это был большой шаг вперед, хотя Фейнман изначально предполагал, что Дирак мог уже сделать то же самое, потому что это ведь было элементарно; да, элементарно, если вас зовут Ричардом Фейнманом. Со временем Фейнману удалось выяснить у Дирака, знал ли тот, как можно использовать его работу 1933 года, если сделать несколько дополнительных математических шагов. Позднее Фейнман вспоминал, что Дирак, лежа на принстонской траве после не самой выдающейся лекции, ответил просто: «Нет, я не знал. Это интересно». Дирак был одним из величайших физиков в истории, но говорил очень мало. Юджин Вигнер, сам принадлежавший к сонму великих, заметил: «Фейнман – это второй Дирак, но на этот раз с человеческим лицом».

Итак, напомним: мы сформулировали правило, которое позволяет зарисовать множество циферблатов, представляющих состояние частицы в некий момент времени. Правило довольно странное: мы наполняем Вселенную бесконечным количеством циферблатов, которые все оказываются связанными друг с другом отношениями, зависящими от тоже довольно странной, но имеющей большое историческое значение величины – действия. Если два или более циферблата оказываются в одном положении в одно и то же время, они суммируются. Правило основано на том, что мы должны предоставить частице свободу перепрыгнуть из любого конкретного места во Вселенной в любое другое место за бесконечно малое время. Мы сразу же сказали: такие абсурдные на вид идеи должны подвергнуться проверке путем столкновения с природой, чтобы убедиться, что получается что‑то разумное. Для начала рассмотрим, как из этой кажущейся анархии возникает нечто очень конкретное. Это один из краеугольных камней квантовой теории – принцип неопределенности Гейзенберга.