Расчет фильтра для первой значимой гармоники и коэффициента искажения синусоидальности кривой напряжения
Найдем коэффициент повышения напряжения на конденсаторе на основной частоте:
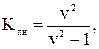 (3.1)
(3.1)
где v– номер гармоники, на которую настроен фильтр.
Определим реактивную мощность конденсаторной батареи:
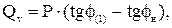 (3.2)
(3.2)
где P=Ud∙Id;
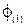 - угол сдвига первой гармоники;
- угол сдвига первой гармоники;
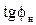 - нормативное значение тангенса (согласно приказу Министерства промышленности и энергетики №49 для сетей 6-20 кВ
- нормативное значение тангенса (согласно приказу Министерства промышленности и энергетики №49 для сетей 6-20 кВ 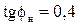 )
)
Рассчитаем емкостное, индуктивное сопротивления v-го фильтра на основной частоте, а также активное сопротивление реактора 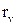 :
:
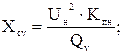 (3.3)
(3.3)
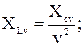 (3.4)
(3.4)
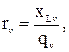 (3.5)
(3.5)
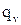 - добротность контура (принимаем
- добротность контура (принимаем 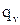 =50)
=50)
Определяем проводимости для каждой гармоники.
Активная составляющая проводимости:
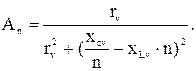 (3.6)
(3.6)
Реактивная составляющая проводимости:
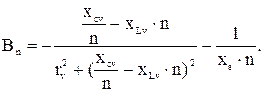 (3.7)
(3.7)
Результирующая проводимость n-ой гармоники:
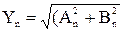 . (3.8)
. (3.8)
Коэффициент искажения синусоидальности кривой напряжения с учетом фильтра:
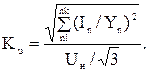 (3.9)
(3.9)
Для того чтобы построить частотную характеристику Z(w) необходимо найти Zэкв.. Для нахождения сопротивления Zэкв определяем параметры схемы замещения (рис.5).
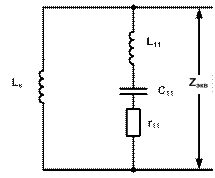
Рис. 5. - Схема замещения элементов сети и фильтра
Индуктивность системы:
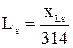 . (3.10)
. (3.10)
Индуктивность фильтра:
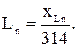 (3.11)
(3.11)
Емкость фильтра:
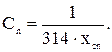 (3.12)
(3.12)
Рассчитываем эквивалентное сопротивление для схемы с фильтром для каждой из гармоник с 1 по 25 (при расчете Zэкв сопротивлением реактора rvпренебрегаем):
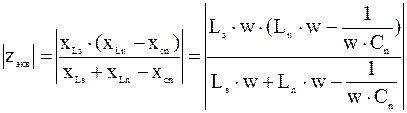 , (3.13)
, (3.13)
где w – угловая частота гармоники:
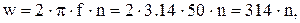 (3.14)
(3.14)
где n – номер гармоники.
Полученные результаты zэкв сводим в матрицу,
Рассчитываем эквивалентное сопротивление для схемы без фильтра:
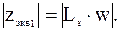 (3.15)
(3.15)
Полученные результаты zэкв сводим в матрицу, состоящую из одного столбца и 25 строк.
Задаем матрицу, состоящую из одного столбца и 25 строк, с номерами гармоник с 1 по 25.
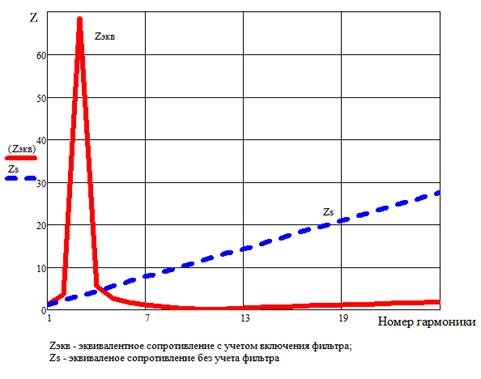
Для построения частотной характеристики задаем график, где ось абсцисс это матрица с номерами гармоник, а ось ординат это две матрицы c эквивалентным сопротивлением для схемы без фильтра и с фильтром.
Находим коэффициенты подавления для тех гармоник которые мы рассматриваем (для одномостовой - 7,9,11; для двухмостовой - 13,23,25):
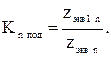 (3.16)
(3.16)
Коэффициент искажения синусоидальности кривой напряжения при включении идеального фильтра:
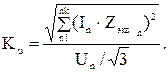 (3.17)
(3.17)
где n– номера исследуемых гармоник.
Полученное значение коэффициента искажения синусоидальности напряжения (3.17) должно незначительно отличаться от коэффициента, рассчитанного по выражению (3.9).
Ток n-ой гармоники в v-ом фильтре.:
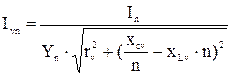 ; (3.18)
; (3.18)
Напряжение на конденсаторе v-ой гармоники
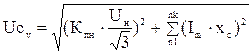 (3.19)
(3.19)
Действующее значение тока фильтра v-ой гармоники:
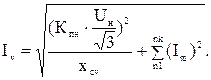 (3.20)
(3.20)
Конденсаторы проверяют по допустимой перегрузочной способности по току и напряжению:
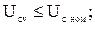
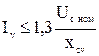 ,
,
где 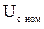 - номинальное напряжение конденсатора в составе v-го фильтра.
- номинальное напряжение конденсатора в составе v-го фильтра.
Пример расчета.
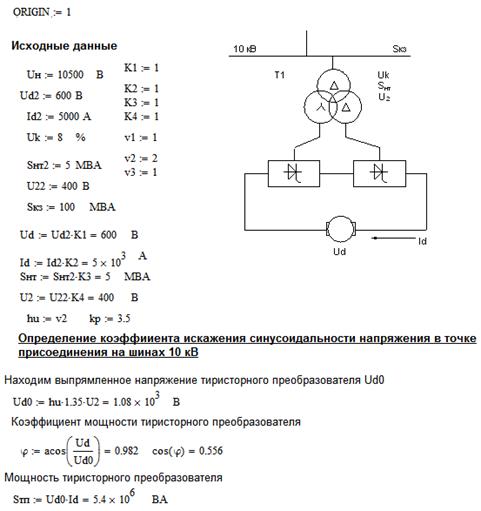




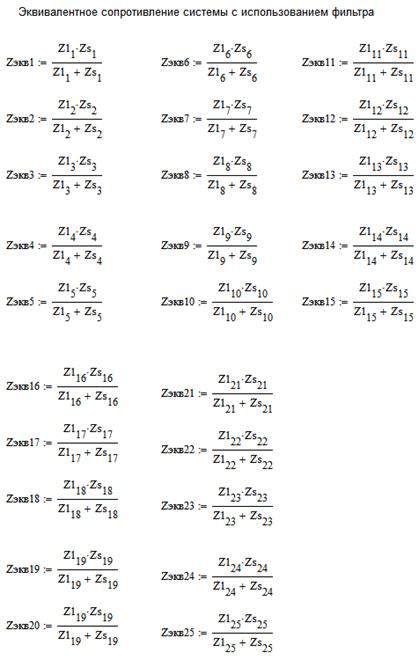


Список литературы
1. Корнилов Г.П., Николаев А.А. , Назарова О.Л. Электромагнитная совместимость: практикум. – Магнитогорск: Изд-во Магнитогорского государственного технического университета им. Г.И.Носова, 2012 – 78 с.
2. ГОСТ 13109-97. Электрическая энергия. Совместимость технических средств электромагнитная. Норма качества электрической энергии в системах электроснабжения общего назначения. // М.: Изд-во стандартов. 1997.
3. Глинтерник С.Р. Электромагнитные процессы и режимы мощных статистических преобразователей. Л.: Наука. 1968. 308 с.
4. Иванов В.С., Соколов В.И. Режимы потребления и качество электроэнергии систем электроснабжения промышленных предприятий. М.: Энергоатомиздат. 1987. 537 с.
