Первое и второе начала термодинамики

Цель: Обобщение и закрепление теоретического материала по теме «Первое и второе начала термодинамики. Термодинамика изопроцессов» и рассмотрение решения задач по данной теме.

Требования к исходному уровню знаний и умений

Знать определения следующих физических понятий:

Ø Внутренняя энергия;

Ø Степени свободы молекулы;

Ø Равновесные и неравновесные процессы;

Ø Адиабатный процесс;

Ø Обратимый и необратимый термодинамические процессы;

Ø Круговой процесс (или цикл);

Ø Прямой и обратный цикл;

Ø Термодинамическая вероятность состояния системы;

Ø Тепловой двигатель;

Ø Холодильная машина

Знать определения следующих физических величин, уметь записать формулы, которыми они определяются, указать единицы измерения и значения.

Ø Внутренняя энергия для произвольной массы т газа;

Ø Теплоемкость;

Ø Удельная теплоемкость вещества;

Ø Молярная теплоемкость;

Ø Теплоемкость при постоянном объеме;

Ø Теплоемкость при постоянном давлении;

Ø Показатель адиабаты (или коэффициент Пуассона);

Ø Термический коэффициент полезного действия для кругового процесса;

Ø Энтропия;

Ø Изменение энтропии идеального газа;

Ø Изменение энтропия в изопроцессах.

Знать формулировку, уметь записать формулы, определяющие следующие физические законы:

Ø Закон равномерного распределения энергии по степеням свободы молекулы;

Ø Первое начало термодинамики;

Ø Применение первого начала термодинамики к изопроцессам;

Ø Второе начало термодинамики (закон возрастания энтропии);

Ø Третье начало термодинамики (теорема Нернста — Планка);

Ø Статистическое истолкование третьего начала термодинамики.

Уметь записать формулу полной работы, совершаемую газом при изменении его объема, и изобразить ее графически.

Уметь записать уравнение Майера и знать его физический смысл.

Уметь записать уравнение адиабатного процесса (уравнение Пуассона).

Уметь изобразить графически прямой или обратный цикл и записать, чему равна работа, совершаемая за этот цикл.

Уметь изобразить графически цикл Карно и назвать процессы, входящие в этот цикл.

Уметь записать и пояснить неравенство Клаузиуса.

Сведения из теории

Средняя полная кинетическая энергия молекулы

,

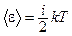где i – число степеней свободы молекулы.

Молярная теплоёмкость газа при постоянном объёме и постоянном давлении соответственно

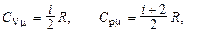
где i – число степеней свободы; R – универсальная газовая постоянная.

Связь между удельной (с) и молярной (С_m) теплоёмкостями

С_m = сm

где m – молярная масса.

Уравнение Майера

С_рm – С_Vm = R.

Внутренняя энергия идеального газа

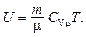
Уравнение адиабатного процесса (уравнение Пуассона)

pV ^g = const, TV ^g-1 = const, T^gp^1-g = const,

где g – показатель адиабаты,

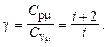
Работа, совершаемая газом при изменении его объёма, в общем случае вычисляется по формуле

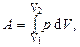
где V₁ и V₂ – начальный и конечный объемы газа.

Работа при изобарном процессе (р = const)

A = p (V₂ – V₁),

при изотермическом (Т = const) –

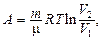
при адиабатном (Q = const) –

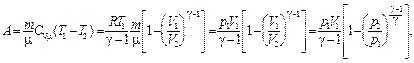
где Т₁, Т₂, V₁, V₂, p₁, p₂ – соответственно, начальные и конечные температура, объём и давление газа.

Первое начало термодинамики

Q = DU + A,

где Q – количество теплоты, сообщённое газу; DU – изменение его внутренней энергии; А – работа, совершённая газом против внешних сил.

Первое начало термодинамики при изобарическом процессе

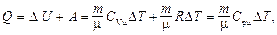
при изохорном (А = 0 ) –

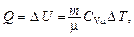
при изотермическом (DU = 0) –

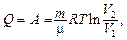
при адиабатическом (Q = 0) –

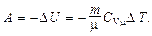
Термический коэффициент полезного действия для кругового процесса (цикла)

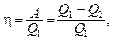
где Q₁ – количество теплоты, полученное системой; Q₂ – количество теплоты, отданное системой; А – работа, совершаемая за цикл.

КПД цикла Карно

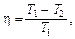
где Т₁ – температура нагревателя; Т₂ – температура холодильника.

Холодильный коэффициент машины, работающей по обратному циклу Карно,

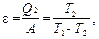
где Q₂ – количество теплоты, отведённое из холодильной камеры; А – совершённая работа; Т₂ – температура более холодного тела (холодильной камеры); Т₁ – температура более горячего тела (окружающей среды).

Изменение энтропии при равновесном переходе системы из состояния 1 в состояние 2

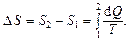
Изменение энтропии идеального газа

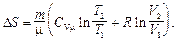
Неравенство Клаузиуса:

.

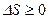Согласно Больцману, энтропия системы и термодинамическая вероятность связаны между собой следующим образом:

,

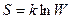где k — постоянная Больцмана.

Теорема Нернста — Планка:

.
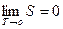