Что такое нормальные условия

1) условия применения средств измерений, при которых влияющие на их показания величины (темп-pa, питающее напряжение и др.) имеют норм. (установленные) значения или находятся в пределах норм. области значений. Н. у. указываются на шкалах средств измерений, в стандартах на них, технич. описаниях иинструкциях к использованию. Пределы допускаемых осн. погрешностей измерений устанавливаются для Н. у. Для электроизмерит. приборов за Н. у. часто принимают следующие: темп-pa— в пределах 20±2°С, питающее напряжение — указанное на шкале ±2%, частота — в пределах 49—51 Гц;

2) физ. условия, определяемые давлением р=101325 Па=760 мм рт. <ст. (норм. атмосфера) и темп-рой273,15К (0°С), при к-рых молярный объём газа V0=2,2414-10-2 м3/моль. Норм. ускорение свободногопадения принимают равным gn= 9,80665 м/с2.

Связь температурных шкал

В шкалах Фаренгейта, Реомюра и Цельсия точке плавления льда t₁ соответствовали +32⁰, 0⁰ и0⁰, а точке кипения воды t₂ – 212⁰, 80⁰ и 100⁰. Основной интервал t₂ – t₁ в этих шкалах делится соответственно на N = 180, 80 и 100 равных частей, и 1/N часть каждого из интервалов называют градусом Фаренгейта – t⁰F, градусом Реомюра t⁰R и градусом Цельсия t⁰C. Таким образом, для шкал, построенных по указанному принципу, градус не является единицей измерения, а представляет собой единичный промежуток – масштаб шкалы.

Для пересчета температуры из одной шкалы в другую используют соотношение:

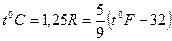(1)

Термодинамическая шкала температур основана на использовании второго закона термодинамики. В соответствии с этим законом коэффициент полезного действия h тепловой машины, работающей по обратному циклу Карно, определяется только температурой нагревателя Т_н и холодильника Т_х и не зависит от свойств рабочего вещества:

(2)

где Q_н и Q_х – соответственно количество теплоты, полученное рабочим веществом от нагревателя и отданное холодильнику.

Кельвином было предложено для определения температуры использовать равенство:

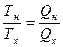(3)

Следовательно, используя один объект в качестве нагревателя, а другой – в качестве холодильника и проведя между ними цикл Карно, можно определить отношение температур объектов путем измерения отношения теплоты, взятой от одного объекта и отданной другому. Полученная шкала температур не зависит от свойств рабочего вещества и называется абсолютной шкалой температур. Чтобы абсолютная температура имела определенное значение, было предложено принять разность термодинамических температур между точками кипения воды Т_кв и таяния льда Т_тлравной 100⁰. Принятие такой разности преследовало цель сохранения преемственности числового значения термодинамической температурной шкалы от стоградусной температурной шкалы Цельсия. Т.О., обозначая количество теплоты, полученной от нагревателя (кипящая вода) и отдаваемой холодильнику (тающий лед), соответственно через Q_кв и Q_тл, и приняв Т_кв – Т_тл = 100, получим:

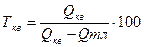и (4)

Для любой температуры Т нагревателя при неизменном значении Т_тл холодильника и количества теплоты Q_тл, отдаваемой ему рабочим веществом машины Карно, будем иметь:

(5)

Уравнение (4) является уравнением стоградусной термодинамической шкалы температур и показывает, что значение температуры Т по данной шкале линейно связано с количеством теплоты Q, полученной рабочим веществом тепловой машины при совершении ею цикла Карно, и, как следствие, не зависит от свойств термодинамического вещества. За один градус термодинамической температуры принимают такую разность между температурой тела и температурой таяния льда, при которой производимая по обратному циклу Карно работа равна 1/100 части работы, совершаемой в цикле Карно между температурой кипения воды и таяния льда (при условии, что в обоих циклах количество теплоты, отдаваемой холодильнику, одинаково).

Из определения к.п.д. следует, что при максимальном значении h=1 должна быть равна нулю Т_х. Эта наименьшая температура была названа Кельвином абсолютным нулем. Температуру по термодинамической шкале обозначают «К».

Термодинамическая шкала температур, основанная на двух реперных точках, обладает недостаточной точностью измерения. Практически трудно воспроизвести температуры указанных точек, т.к. они зависят от давления, а также от содержания солей в воде. Поэтому Кельвин и Менделеев высказали соображение о целесообразности построения термодинамической шкалы температур по одной реперной точке.

Консультативный комитет по термометрии Международного комитета мер и весов в 1954 году принял рекомендацию о переходе к определению термодинамической шкалы с использованием одной реперной точки – тройной точки воды (точки равновесия воды в твердой, жидкой и газообразной фазах), которая легко воспроизводится в специальных сосудах с погрешность не более 0,0001 К. Температура этой точки принята равной 273, 16 К, т.е. выше температуры таяния льда на 0,01 К. Такое число выбрано для того, чтобы значения температур по новой шкале практически не отличались от старой шкалы Цельсия с двумя реперными точками. Второй реперной точкой является абсолютный нуль, который практически не реализуется, но имеет строго фиксированной положение.

В 1967 году XIII Генеральная ассамблея по мерам и весам уточнила определение единицы термодинамической температуры в следующей редакции: «Кельвин – 1/273,16 часть термодинамической температуры тройной точки воды». Термодинамическая температура может быть выражена также в градусах Цельсия:

t = T – 273,15 K (6)

Идеальный газ

Идеальный газ- это физическая модель газа, взаимодействие между молекулами которого пренебрежительно мало.

На основании использования основных положений молекулярно-кинетической теории было получено основное уравнение МКТ идеального газа, которое выглядит так: 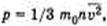, где р — давление идеального газа, m0 — масса молекулы, 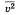среднее значение концентрация молекул, квадрата скорости молекул.
Обозначив среднее значение кинетической энергии поступательного движения молекул идеального газа 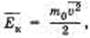получим основное уравнение МКТ идеального газа в виде:

Идеальнымназывается газ, взаимодействие, между молекулами которого пренебрежимо мало и состояние которого описывается уравнением Клапейрона-Менделеева.

Модель идеального газа.

1. Собственный объём молекулгаза пренебрежимомалпо сравнению с объёмом сосуда.

2. Между молекулами газа отсутствует силы взаимодействия.

3. Столкновениямолекул газа между собой и со стенками сосудаабсолютно упругие.

Взаимодействие между молекулами всякого газа становится пренебрежимо слабым при малых плотностях газа, при большом разрежении. Такие газы как воздух, азот, кислород, даже при обычных условиях, т.е. при комнатной температуре и атмосферном давлении мало отличаются от идеального газа. Особенно близки к идеальному газу гелий и водород.

Не следует думать, что взаимодействиемежду молекулами идеального газа вовсеотсутствует. Напротив, его молекулы сталкиваются друг с другом и эти столкновениясущественны для установления определённых тепловых свойств газа. Но столкновения проходятнастолько редко, чтобольшую часть времени молекулы движутся как свободные частицы.

Именно столкновения между молекулами позволяют ввести такой параметр как температура. Температура телахарактеризует энергию, с которой движутся его молекулы. Для идеального газа в равновесных условияхабсолютная температура пропорциональна средней энергии поступательного движения молекул.

Определение.Макроскопическойназывается система, образованная огромным числом частиц (молекул, атомов).Параметры, характеризующие поведение системы (например, газа), как целого, называется макропараметрами. Например, давлениеР, объёмVи температураТгаза – макропараметры.

Параметры, характеризующие поведение отдельных молекул(скорость, масса и т.п.) называетсямикропараметрами.

Уравнение идеального газа:

Давление идеального газа
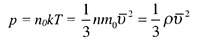