Физические основы эксперимента. Физические величины, количественно характеризующие отдельные молекулы, называются микропараметрами

Физические величины, количественно характеризующие отдельные молекулы, называются микропараметрами. К ним относятся координаты молекул, их импульсы, скорости и т.д.

Физические величины, характеризующие тело в целом называются макропараметрами. Это температура, давление, концентрация молекул и т. д.

Состояние системы, заданное микропараметрами ее молекул, называют микросостоянием. Состояние системы, характеризующееся набором макропараметров, называют макросостоянием. Количество микросостояний, которым может быть реализовано данное макросостояние, называется термодинамической вероятностью Ω (или статическим весом).

В данной лабораторной работе рассматривается только один микропараметр молекул (шаров) - положение (координата) молекулы, которое может иметь всего два значения : в «левой» или «правой» половине сосуда (коробки). Макросостояние системы шаров, когда их число в «левой» и «правой» половинных одинаково, является равновесным. Любое другое макросостояние, когда количество шаров одного цвета не одинаково в разных половинах коробки, является в той или иной степени неравновесным. Нетрудно понять, что любое из этих состояний, можно реализовать разными вариантами перестановок шаров одного цвета между правой и левой половинами коробки. Как это следует из определения, количество таких перестановок и есть термодинамическая вероятность Ω данного состояния.

В [1] для данной физической ситуации термодинамическая вероятность определяется как

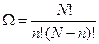, (1)

где N- количество шаров одного цвета в коробке, n- количество шаров в одной половине коробки, (N-n)- количество шаров в другой половине коробки.

Отсюда следует, что в крайне неравновесном состоянии, когда все шары находятся в одной половине коробки (n=0), термодинамическая вероятность имеет минимальной значение Ω=1 (т.к. 0! принимается равным единице). Т.е. такое макросостояние реализуется всего одним способом. В равновесном состоянии, когда n=N/2, термодинамическая вероятность Ω максимальна. Значит в процессе перехода системы в равновесное состояние Ω растет от 1 до максимального значения Ω_равн (рис. 2).

Рис. 2.

Однако в принципе этот рост не монотонный (см. рис.2), т.к. соударения молекул в процессе теплового движения (случайные соударения шаров в данном эксперименте) приводят к случайным изменениям Ω. В частности, поэтому в равновесном состоянии термодинамическая вероятность со временем случайным образом отклоняется от Ω_равн (см. рис. 2). Такие отклонения называются флуктуациями.

Абсолютная флуктуация Ω относительно равновесного состояния определяется как

∆Ω = Ω_равн - Ω_{τ ,} (2) где Ω_τ - термодинамическая вероятность в данный момент времени τ. Относительная флуктуация термодинамической вероятности: 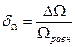. Методами статистики показано [1], что эта величина пропорциональна ~ 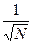. Т.е. флуктуации велики в системах с небольшим количеством молекул. В реальных системах, состоящих из огромного числа молекул, флуктуации пренебрежительно малы.

Термодинамические вероятности молекулярных систем имеют очень большие числовые значения, т.к. количество молекул, из которых они состоят чрезвычайно велико (например, в 1 см³ воздуха при н.у. содержится ~2·10¹⁹ шт. молекул). Это создает определенные трудности расчета величины Ω и ее изменения. Поэтому на практике для количественной оценки макросостояния системы используется т. н. энтропия S,которая в соответствие с формулой Больцмана определяется как: 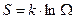, (3)

где 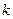- постоянная Больцмана.

Формула Больцмана показывает, что в соответствие со свойствами термодинамической вероятности Ω, описанными выше, энтропия в крайне неравновесном состоянии (все шары-молекулы одного цвета находятся в одной половине коробки) равна 0, в процессе диффузии энтропия будет возрастать, в равновесном состоянии энтропия достигнет максимального значения, далее энтропия будет оставаться постоянной с точностью до флуктуаций.

Все эти изменения энтропии можно экспериментально проверить на данной лабораторной установке, фиксируя во времени изменения положений шаров по площади колеблющейся коробки. Тем самым можно проверить выполнимость одного из фундаментальных физических законов - второго начала термодинамики, которое формулируется следующим образом:

В замкнутой системе наиболее вероятен такой процесс, в котором энтропия возрастает.