Теплоємність газів і число ступенів вільності. Закон рівномірного розподілу кінетичної енергії за ступенями вільності
Для того, щоб пояснити розбіжність теорії і експерименту для багатоатомних газів, потрібно в деякій мірі відмовитися від звичайної моделі ідеального газу. Ми вважали, що молекули такого газу являли собою матеріальні точки, розмірами яких ми нехтували і які рухалися тільки поступально.
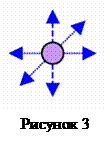 Одноатомна молекула. Отже, якщо молекула є матеріальною точкою, то її положення в просторі повністю визначається трьома незалежними координатами (x, y, z), тобто вона має три ступені вільності (рис.3). Окрім цього, ці три ступені вільності відносяться лише до поступального руху, оскільки не має фізичного змісту говорити про обертовий рух матеріальної точки.
Одноатомна молекула. Отже, якщо молекула є матеріальною точкою, то її положення в просторі повністю визначається трьома незалежними координатами (x, y, z), тобто вона має три ступені вільності (рис.3). Окрім цього, ці три ступені вільності відносяться лише до поступального руху, оскільки не має фізичного змісту говорити про обертовий рух матеріальної точки.
Як ми знаємо, енергія поступального руху молекул ідеального (одноатомного) газу:
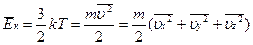
В результаті хаотичності молекулярних рухів можна вважати, що середні значення кінетичних енергій за трьома напрямками (x, y, z) дорівнюють одне одному:
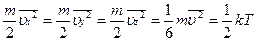
Таким чином, на кожний ступень вільності одноатомної молекули припадає енергія, яка дорівнює 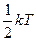 .
.
Більш того, в класичній статфізиці Больцманом було доведено, що, коли молекула має, окрім поступальних, і інші ступені вільності, то на кожну з них також припадає енергія 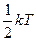 .
.
Отже, закон рівномірного розподілу кінетичної енергії за ступенями вільності читається так:
Якщо термодинамічна система знаходиться в стані теплової рівноваги при температурі T, то середня кінетична енергія рівномірно розподілена за всіма ступенями вільності і для кожної з них дорівнює 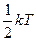 .
.
Таким чином, якщо число ступенів вільності для молекули дорівнює і, то середня енергія молекули:
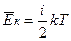
Тобто внутрішня енергія довільної маси газу дорівнює:
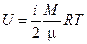 (17)
(17)
Для молярних теплоємностей газу отримаємо вирази:
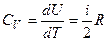 (18)
(18)
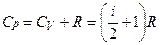 (19)
(19)
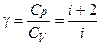 (20)
(20)
Як і потрібно було очікувати, для одноатомних газів, використавши формулу (18)-(20), отримаємо:
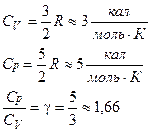
Двохатомна молекула з жорстким зв’язком між атомами. У випадку, коли молекула газу складається з двох атомів, розташованих на деякій фіксованій відстані один від одного, то чисто ступенів вільності і=5. Дійсно, для опису розташування у просторі такої системи достатньо завдати три координати (x, y, z) центра мас, які визначатимуть поступальний рух системи, і дві координати (кути повороту), які визначатимуть можливі кути обертання молекули навколо осей y і z. Обертання навколо вісі x, на якій розташовані центри мас обох атомів як матеріальних точок, позбавлене змісту. Отже, дві матеріальні точки, жорстко пов’язані між собою, мають 5 ступенів вільності (і=5).
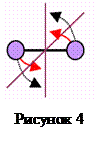 Тоді при і=5 для теплоємності двохатомних газів матимемо, згідно (17) - (20):
Тоді при і=5 для теплоємності двохатомних газів матимемо, згідно (17) - (20):
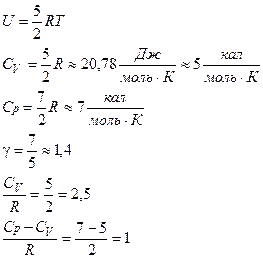
Це задовільно узгоджується з експериментальними даними для ряду двохатомних газів, виключаючи Cl2.
Тобто атоми в молекулах таких газів (O2, N2, H2, CO та ін.) дійсно жорстко пов’язані між собою і не збуджують коливальний рух поблизу центра мас.
Двохатомна молекула з нежорстким зв’язком між атомами. Якщо два атоми (дві матеріальні точки) пов’язані так, що відстань між ними може змінюватись, то число ступенів вільності дорівнює 6 (3 ступені поступального руху, 2 обертового і 1 коливального). Якщо для описання коливального руху атомів у молекулі 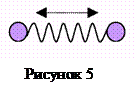 застосовувати модель гармонійного осцилятору, то середню потенціальну енергію атомів можна вважати рівною їхньої середньої кінетичної енергії. Тоді повну енергію, що приходиться на одну коливальну ступінь вільності, можна вважати рівною подвоєної її кінетичної енергії (
застосовувати модель гармонійного осцилятору, то середню потенціальну енергію атомів можна вважати рівною їхньої середньої кінетичної енергії. Тоді повну енергію, що приходиться на одну коливальну ступінь вільності, можна вважати рівною подвоєної її кінетичної енергії ( 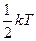 у вигляді кінетичної енергії, а також
у вигляді кінетичної енергії, а також 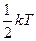 у вигляді потенціальної енергії). Тому при врахуванні коливальних ступенів вільності необхідно енергію молекули збільшувати на величину
у вигляді потенціальної енергії). Тому при врахуванні коливальних ступенів вільності необхідно енергію молекули збільшувати на величину 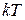 , а число і відповідно на два на кожну коливальну ступінь вільності. Цим відрізняється врахування коливального руху від врахування поступального і обертового рухів, де на кожну ступень вільності приходиться енергія
, а число і відповідно на два на кожну коливальну ступінь вільності. Цим відрізняється врахування коливального руху від врахування поступального і обертового рухів, де на кожну ступень вільності приходиться енергія 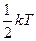 .
.
В загальному випадку
і=іпост.+іоберт.+2іколив.,
де іпост., іоберт., іколив. – числа відповідних ступенів вільності. Тоді при і=3+2+2×1=7:
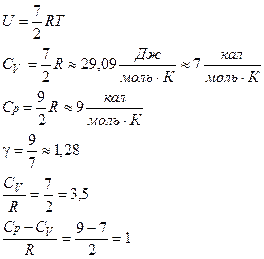
Трьохатомна молекула з жорсткими зв’язками між атомами має три ступені вільності поступального руху плюс три ступені вільності обертового руху.
Отже, для трьохатомного (і більше) газу і=6:
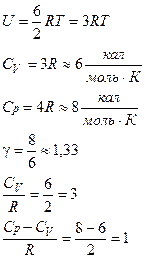
Таким чином, теплоємність CV усіх багатоатомних молекул (починаючи з трьохатомних) повинна бути CV=3R, а експеримент дає дещо більші значення
для CO2 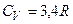
для H2O 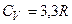
для C2H4 та ін. 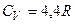
Ці перевищення експериментальних значень над теоретичними неможливо пояснити похибкою експерименту.
Зробимо висновки про розходження класичної теорії теплоємності ідеального газу з експериментом:
а) Названі вище прості формули добре збігаються з експериментом лише для одноатомних газів (окрім Cl2) для дослідів при температурах, близьких до кімнатної, і тисках порядку атмосферного.
б) У трьохатомних газів спостерігаються систематичні відхилення експерименту від значень, передбачених теорією.
в) Нарешті, за класичною теорією Cp і CV не повинні залежати від температури. Експеримент показав, що залежність CV=f(T) має місце, що суперечить формулам класичної теорії.
Відзначимо, що безпосереднє використання виразів (17) - (20) для багатоатомних газів, у молекулі яких атоми зв'язані не жорстко, не є коректним. Це пояснюється тим, що коливальні ступені волі мають при нормальних умовах значно меншу, ніж 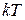 , енергію. Тільки при досить високій температурі, порядку 103 К, енергія коливальних ступенів волі стає порівнянною с
, енергію. Тільки при досить високій температурі, порядку 103 К, енергія коливальних ступенів волі стає порівнянною с 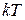 . При низьких температурах (порядку 10 К) закон рівнорозподілу стає не застосовним і для обертальних ступенів волі. Це пов'язано з тим, що закони класичної статистичної механіки, на яких заснований доказ закону про рівнорозподіл енергії по ступенях волі, мають дуже обмежене застосування для атомно-молекулярних систем. Тут необхідне застосування квантовомеханічних законів.
. При низьких температурах (порядку 10 К) закон рівнорозподілу стає не застосовним і для обертальних ступенів волі. Це пов'язано з тим, що закони класичної статистичної механіки, на яких заснований доказ закону про рівнорозподіл енергії по ступенях волі, мають дуже обмежене застосування для атомно-молекулярних систем. Тут необхідне застосування квантовомеханічних законів.
Однак для газів, що знаходяться при нормальних умовах, закон рівнорозподілу може бути застосований для поступальних і обертальних ступенів волі з досить високим ступенем точності.
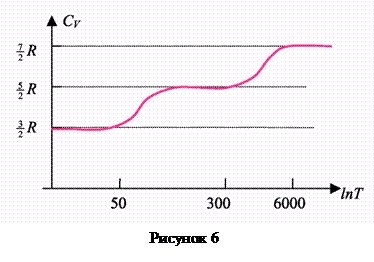 |
Розглянемо залежність теплоємності від температури, яка приведена для 2-х атомної молекули (типу Н2) на рис. 6. З рисунку видно, що теплоємність змінюється з температурою. Згідно теорії для двохатомного газу CV=5/2R (при збудженні коливань можливо 7/2R). Але 3/2R бути не може (при низьких температурах). Розуміння такої залежності було досягнуте в квантовій фізиці, де враховується, що енергія молекул приймає дискретні значення.
Хай відстань між двома рівнями енергії дорівнює 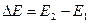 .Тоді якщо внутрішня енергія теплового руху така, що
.Тоді якщо внутрішня енергія теплового руху така, що 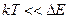 , то цієї енергії не вистачає, щоб збудити рівень енергії Е2 і відповідний ступінь вільності. Тобто при розрахунку теплоємності треба враховувати ступені вільності, пов'язані тільки з рівнем енергії Е1. Рівень Е2 в теплоємності не виявляється.
, то цієї енергії не вистачає, щоб збудити рівень енергії Е2 і відповідний ступінь вільності. Тобто при розрахунку теплоємності треба враховувати ступені вільності, пов'язані тільки з рівнем енергії Е1. Рівень Е2 в теплоємності не виявляється.
Для типової двоатомної молекули температури для повного включення різних ступенів вільності наступні:
для поступального руху: 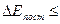 50 К;
50 К;
для обертального руху: 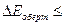 300 К;
300 К;
для коливального руху: 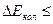 6000 К.
6000 К.
Із зростанням температури відбувається включення ступенів свободи. Тільки при достатньо високих температурах kT газ поводиться відповідно до класичного закону рівнорозподілу.
