Методы обработки результатов измерений, содержащие случайную ошибку

Наиболее вероятное значение измеряемой величины – её среднее арифметическое

(1)

Средней квадратичной ошибкой отдельного результата измерения называется величина

(2)

При , стремится к постоянному пределу :

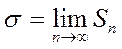(3)

Величина называется дисперсией измерения. Величина служит основным параметром, определяющим вид кривой распределения случайных ошибок. Нормальный закон распределения ошибок (гаусовское распределение) выражается формулой

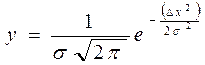(4)

где 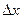- отклонение от истинного значения и 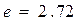- основание натурального логарифма.

Среднеквадратичной ошибкой среднего арифметического называется величина

(5)

Это фундаментальный закон возрастания точности при росте числа измерений. Вероятность того, что (a), истинное значение 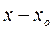находится внутри некоторого интервала от 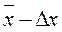до называется коэффициентом надежности.

Окончательный результат измерений запишется в виде

(6)

Множители, определяющие величину интервала надежности в долях в зависимости от a и n , называются коэффициентами Стьюдента, они обозначаются a,t и находятся из таблицы (См. Р.И.Солоухин.Методы физических измерений. “Наука”, 1975).

Конечный результат в данном случае представляется в виде

(7)

Из сказанного следует:

Величина среднеквадратичной ошибки позволяет вычислить вероятность попадания истинного значения измеряемой величины в любой интервал вблизи среднего арифметического.

При ¥, , 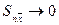т.е. интервал, в котором с заданной вероятностью находится истинное значение , стремится к нулю с увеличением числа измерений. Это означает возрастание точности при росте числа измерений. Казалось бы, увеличивая n, можно получить результат с любой степенью точности . Однако точность существенно увеличивается лишь до тех пор, пока случайная ошибка не станет сравнимой с систематической. Дальнейшее увеличение числа измерений нецелесообразно, т.к. конечная точность результата будет зависеть только от систематической ошибки. Зная величину систематической ошибки, нетрудно задаться допустимой величиной случайной ошибки, взяв ее, например, равной 10% от систематической. Задавая для выбранного таким образом интервала надежности определенное значение a, нетрудно найти необходимое число измерений, гарантирующее малое влияние случайной ошибки на точность результата.

При обработке результатов измерений предлагается следующий порядок операций. При прямых измерениях:

1. Результаты каждого измерения записываются в таблицу.

2. Вычисляется среднее значение из n измерений

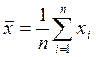
3. Находятся погрешности отдельного измерения

4. Вычисляются квадраты погрешностей отдельных измерений

5. Определяется среднеквадратичная погрешность среднего арифметического

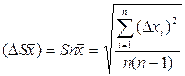
6. Задается значение надежности .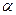

7. Определяется коэффициент Стьюдента для надежности 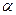и числа произведенных измерений.

8. Находится погрешность результата измерений.

9. Окончательный результат записывается в виде:

10. Оценивается относительная погрешность результата измерений

Порядок выполнения работы

1. Собрать схему. Ознакомьтесь с описанием звукового генератора и счетчика импульсов.

2. Подать на пересчетное устройство со звукового генератора сигнал.

3. Подсчитать число импульсов за 5-10 секунд (время отсекать кнопкой «Стоп» пересчетного механизма). Измерения проделать 100 раз для каждой частоты.

4. Провести обработку результатов измерений по указанной выше методике.

5. Выбрать масштаб и построить график экспериментального распределения ошибок: по оси Х отложить величину отклонения от среднего, по оси У – относительное число измерений с отклонением в заданном интервале. На том же графике нанести кривую Гаусса с экспериментально определенной дисперсией.

6. . Найти ошибку измерений для n=100, 50, 10, используя коэффициенты Стьюдента.

ЛИТЕРАТУРА

1. Зайдель А. Н. Элементарные оценки ошибок измерений. М., 1965.

2. Физический практикум под ред. В. И. Ивероновой. М., «Наука», 1968.

3. Р. И. Солоухин. Методы физических измерений. «Наука» СО АН 1975.

4. Дж. Сивайрс. Практическая физика. М., 1972.