Ансамбли различаемых сигналов

Ансамбли различаемых сигналов, т.е. группы М однородных сиг­налов, должны отличаться по какому-то параметру или признаку – форме, времени, частоте, пространству, поляризации (рис. 12.12):

,

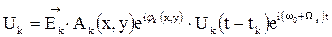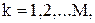
где 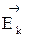- вектор напряженности электромагнитного поля К-го сигнала, характеризующий его поляризационную структуру; 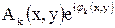– амплитудно-фазовое распределение К-го сигнала на раскрыве антенны, характеризующее пространственную структуру сигнала; 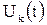– закон модуляции К-го сигнала, характеризующий форму сигнала; t_k – время задержки К-го сигнала относительно некоторого опорного момента времени; W_k – частотный сдвиг К-го сигнала относительно некоторой несущей частоты w₀.

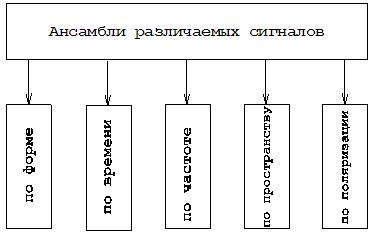
Рис. 12.12. Классификация различных сигналов

Условием различимости сигналов является их взаимная ортогональ­ность

.

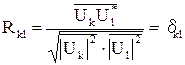Различаться в этом смысле по поляризации могут только два сигнала (М=2), относящиеся к двум взаимно ортогональными по поляризации составляющим произвольного поляризационного базиса 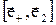. Различаться по времени могут М>>1 cигналов. Если на интерва­ле временного уплотнения Т_упл уменьшается нe менее М элементов, временного разрешения сжатых по времени широкополосных сложных сигналов Dt_z=1/Df₀ (рис. 12.13):

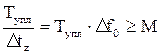
Различаться по частоте могут M>>1 сигналов, если на интервале частотного уплотнения F_упл умещается не менее M элементов частот­ного разрешения сжатых по спектру длинноимпульсных сложных сигналов DF=1/T₀ (риc. 12.14):

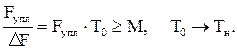
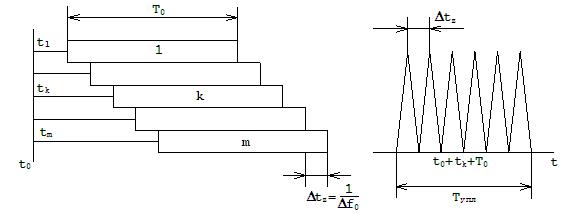
а) до сжатия по времени б) после сжатия по времени

Рис. 12.13. Пояснение различения сигналов по времени

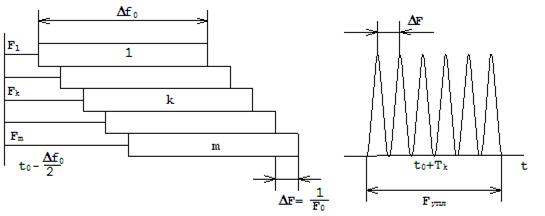
а) до сжатия по частоте б) после сжатия по частоте

Рис. 12.14. Пояснение различения сигналов по частоте

Различаться по пространству могут М>>1 сигналов, если в диапазоне телесного углового уплотнения Y_упл уметается не менее М элементов телесного углового разрешения DY=l²/S_a (рис. 12.15):

.

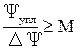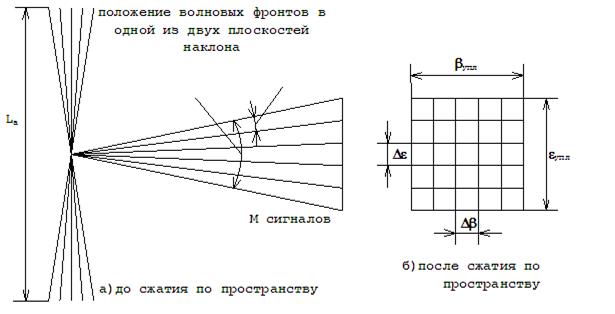
Рис. 12. 15. Пояснение различения сигналов по пространству

Различаться по форме могут М>>1 сигналов с разными законами внутриимпульсной модуляции (КФМ сигналы с различными ходами, ЧМ сиг­налы с различными законами частотной модуляции и т.п.).

Решающее правило

Рассмотрим решавшее правило задачи распознавания-различения по аналогии с задачей обнаружения. Задача обнаружения двухальтернативна, так как при обнаружении выносится одно из двух решений: "есть сигнал" или "нет сигнала". В отличие от нее задача распоз­навания многоальтернативна: выносится решение о принадлежности портрета или сигнала к одному из М классов.

Решение задачи обнаружения по критерию минимума среднего рис­ка приводит к необходимости сравнения так называемого отношения правдоподобия

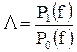
с порогом

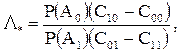
который зависит от априорных вероятностей наличия P(A₁) и отсутствия P(A₀) сигнала и стоимостей C_kl принятия К-го решения при l-ом условии.

При этой правило решения выглядит следующим образом:

если L³L_*, то принимается решение А^*₁,

если L<L_*, то принимается решение А^*₀.

Аналогично при решении многоальтернативной задачи распознавания-различения с позиций минимального вредного риска правило решения определяется следующим выражением:

если ,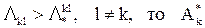

где 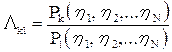– отношение правдоподобия затупленного портрета (сигнала) К-го класса на фоне зашумленного портрета (сигнала) l-го класса,

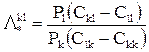– порог сравнения отношения правдоподобия L_kl,

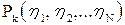– многомерная плотность вероятности комплексных амплитуд принятого сигнала по элементам пространства распознавания (различения) при условии наличия порт­рета (сигнала) К-го класса

,

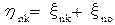x_no – фоновая (помеховая) составляющая принятого сигнала по элементам пространства распознавания (различения),

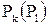– априорные вероятности появления портретов (сигналов) К-го (l-го) класса.

Полагая стоимости правильных решений равными нулю (C_kk=C_ll=0), стоимости ошибочных решений одинаковыми (C_kk=C_ll, l¹k), а появление портретов (сигналов) разных классов равновероятным (Р_k=Р_l), правило решения представляется в виде:

если 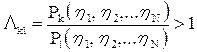для всех l¹k, то А^*_k.

Процедура принятия решения согласно этому правилу состоит в следующем. Производится обработка комплексных амплитуд h_n принятого сигнала по элементам пространства распознавания (различения) в соответствии с алгоритмом, рекомендуемым отношением прав­доподобия L_kl. Номер "К", при котором случайная величина – от­ношение правдоподобия окажется больше единицы для всех l¹k и является номером гипотезы, которую можно принять с наименьший средним риском. Таким образом, решение принимается на основе по­следовательной проверки всех гипотез путем сравнения каждой из них со всеми остальными.

Для того чтобы с наименьшим риском ответить на вопрос о на­личии портрета (сигнала) 1-го класса, необходимо проверить отно­шения правдоподобия L_1l для всех l¹1 (их число равно M-1). Если все L_1l окажутся больше единицы, то при наименьшем среднем риске следует принять, гипотезу о наличии портрета (сигна­ла) 1-го класса. Если неравенства не соблюдены, то проверяются аналогичным образом отношения правдоподобия L_2l(l¹2), L_3l(l¹3) и т.д., вплоть до L_ml(l¹m). Максимально возможное число проверок равно таким образом М(М-1).

Процедуру принятия решения можно существенно упростить. Дей­ствительно, представив правило решения в виде:

если ,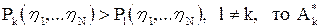

и, разделив левую и правую части неравенства на многомерную плот­ность вероятности комплексных амплитуд принятого сигнала по эле­ментам пространства распознавания (различения) при условии отсут­ствия всякого портрета (сигнала) 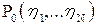, когда h_N=x_n0, находим правило решения в несколько иной форме:

если ,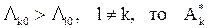

где 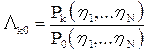– отношение правдо­подобия зашумленного портрета (сигнала) К-го класса. Это правило решения прежде всего убеждает в том, что число проверок сокращает­ся до числа проверяемых гипотез M-1. Во-вторых, это правило реше­ния убеждает в преемственности задач обнаружения и распознавания. В самом деле, левая и правая части неравенства (правила решения) свидетельствуют о том, что вначале необходимо осуществить опти­мальную пространственно-временную и поляризационную обработку каж­дого элемента h_n портрета (n=1,…N) в соответствии с алгоритмом, рекомендуемым отношением правдоподобия

,

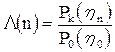и, распределив комплексные амплитуды принятого сигнала по элемен­там пространства распознавания (различения), осуществить совмест­ную обработку элементов каждого К-го портрета (сигнала) (k=1,…M) в соответствии с алгоритмом, рекомендуемым отношением правдоподобия

.
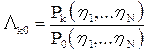