Методика обработки результатов эксперимента
Первоначально определяется расход воздуха через установку. Для этого необходимо перевести показания ротаметра в массовый расход воздуха.
Градуировочная шкала ротаметра приведена в табл. 1.
Таблица 1. Градуировочная шкала ротаметра
| N, число делений | |||||
Расход 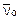 , л/ч , л/ч | |||||
| Расход при параметрах воздуха: to=24 oC, Po=755 мм рт. ст., ρо=1,18 кг/м3 |
Перерасчет объемного расхода воздуха с параметров градуировочной шкалы ротаметра на действительные параметры воздуха выполняется по формуле
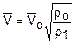 , (4.1)
, (4.1)
где 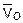 – объемный расход воздуха по градуировочной таблице ротаметра, л/ч;
– объемный расход воздуха по градуировочной таблице ротаметра, л/ч;
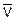 – объемный расход воздуха в пересчете на параметры воздуха перед ротаметром в опыте, л/ч;
– объемный расход воздуха в пересчете на параметры воздуха перед ротаметром в опыте, л/ч;
ρо – плотность воздуха по градуировочной таблице ротаметра, кг/м3;
ρ1 – плотность воздуха при его параметрах на входе в ротаметр, кг/м3.
Плотность воздуха на входе в ротаметр определяется по уравнению состояния идеального газа
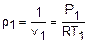 , (4.2)
, (4.2)
где Р1 – давление воздуха на входе в ротаметр, принимается равным атмосферному давлению;
Т1 – температура воздуха на входе в ротаметр.
Массовый расход воздуха G, кг/с, через установку рассчитывается по уравнению
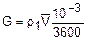 . (4.3)
. (4.3)
Полученную величину расхода воздуха записывают в таблицу результатов обработки опытных данных (см. табл. 2).
Таблица 2. Результаты обработки опытных данных
| № опыта | Uн, В | I, А | I Uн, Вт | t1, оС | t2, оС | ∆t, оС | G, 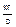 | cрm, 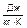 |
Далее определяется электрическая мощность нагревателя по напряжению Uн и току I. Электрический ток, проходящий через нагреватель, рассчитывается по формуле
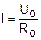 , (4.4)
, (4.4)
где Ro – образцовое сопротивление 0,1 Ом, подключенное последовательно с нагревателем;
Uo – напряжение на образцовом сопротивлении.
Определение средней массовой изобарной теплоемкости воздуха может выполняться двумя способами [3].
Определение теплоемкости без учета внешнего теплообмена установки
В этом варианте расчета считается, что вся теплота нагревателя идет только на нагрев воздуха и соответствует выражению
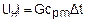 , (4.5)
, (4.5)
где ∆t – разница температур воздуха на выходе из сосуд Дюара t2 и входе в него t1.
Расчетное выражение средней массовой изобарной теплоемкости воздуха в этом случае будет соответствовать виду
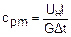 . (4.6)
. (4.6)
Определение теплоемкости с учетом внешнего теплообмена установки
При наличии передачи или получения теплоты воздухом со стороны внешней среды в правую часть выражения (4.5) необходимо добавить второе слагаемое
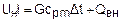 , (4.7)
, (4.7)
где Qвн – внешняя теплота, подведенная к воздуху или отведенная от него.
Внешняя теплота может быть как положительной, так и отрицательной. При Qвн>0 происходят потери теплоты во внешнюю среду через стенки сосуда Дюара или часть теплоты электронагревателя идет на прогрев стенок этого сосуда. В случае когда Qвн<0, нагрев воздуха частично осуществляется за счет того, что сосуд Дюара имеет температуру выше, чем температура воздуха в нем (такое возможно, когда опыт проводится на неостывшей установке).
Для учета внешней теплоты при определении теплоемкости принимаем в качестве постоянных расход воздуха, теплоемкость воздуха и внешнюю теплоту. Определение теплоемкости в этом случае ведется по результатам двух опытов. Записав уравнение (4.7) для двух опытов как
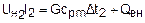 ,
,
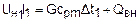
и вычтя из первого второе, получим соотношение
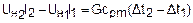 . (4.8)
. (4.8)
Расчетное выражение средней массовой изобарной теплоемкости воздуха в этом случае выразится как
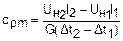 . (4.9)
. (4.9)
Рекомендуется выполнить расчеты средней массовой изобарной теплоемкости воздуха по обеим методикам.
Далее необходимо сравнить найденную величину cpm с ее значением из справочных данных [1] и оценить относительную погрешность опытных результатов по сравнению со справочными данными.
Таблица 3. Теплоемкости воздуха
| Средние теплоемкости воздуха | ||||||
| cpm, | cvm, | mcpm, | mcvm, | c¢pm, | c¢vm, | к |
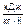 | 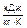 | 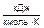 | 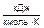 | 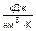 | 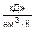 | |
| Теплоемкости идеального воздуха | ||||||
| cp, | cv, | mcp, | mcv, | c¢p, | c¢v, | к |
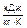 | 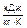 | 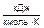 | 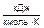 | 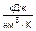 | 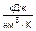 | |
На основании определенной опытным путем cpm вычислить величины средних теплоемкостей воздуха: массовой при постоянном объеме cvm; объемных при постоянном давлении и при постоянном объеме при нормальных условиях c¢pm и c¢vm; мольных mcpm и mcvm и величину к = cpm/cvm. Сравнить данные теплоемкости с соответствующими теплоемкостями идеального двухатомного воздуха, используя расчетные выражения этих теплоемкостей, полученных в соответствии с молекулярно-кинетической теорией идеального газа [2]. Результаты расчетов свести в таблицу (см. табл. 3).
