Требования по технике безопасности. 3. Экспериментальная часть ..7
Содержание
1. Цель работы ………………………………………………………………4
2. Теоретическая часть……………………………………………………...4
3. Экспериментальная часть………………………………………………..7
4. Требования по технике безопасности…………………………………..8
5. Порядок выполнения работы……………………………………………8
6. Требования к отчету…………………………………………………….12
7. Контрольные вопросы…………………………………………………..13
Список литературы………………………………………………………...13
Лабораторная работа № 69
ИЗУЧЕНИЕ ДИФРАКЦИИ СВЕТА НА ДВУМЕРНОЙ ДИФРАКЦИОННОЙ РЕШЕТКЕ
Цель работы
1.1. Ознакомление с дифракцией света на двумерной дифракционной решетке и теорией расчета её дифракционной картины.
1.2. Экспериментальное определение параметров двумерной дифракционной решетки.
Теоретическая часть
Теория одномерной дифракционной решетки достаточно подробно рассматривается в курсе общей физики. Положение главных максимумов в дифракционной картине такой решетки в случае нормального падения лучей определяется выражением
d sin j = ± n l, (2.1)
где d – постоянная решетки, j – угол дифракции, отсчитываемый от нормали к поверхности решётки, l – длина световой волны, n – целое число, определяющее порядок дифракционногомаксимума.
 |
Рис. 2.1. Двумерная дифракционная решетка
В простейшем случае двумерной дифракционной решеткой являются одномерные перпендикулярные решетки с периодами d1 и d2 (рис. 2.1). Дифракцию на такой решетке можно рассматривать как последовательную дифракцию лучей на двух расположенных одна за другой одномерных решетках с взаимно перпендикулярным расположением штрихов. Узкий пучок монохроматического света, пройдя через первую решетку с вертикальными штрихами, должен дать совокупность максимумов вдоль горизонтальной линии. Световой пучок, соответствующий каждому максимуму, проходя через вторую решетку, распадается на новую совокупность световых пучков, дающих максимумы вдоль вертикальной линии (рис. 2.2).
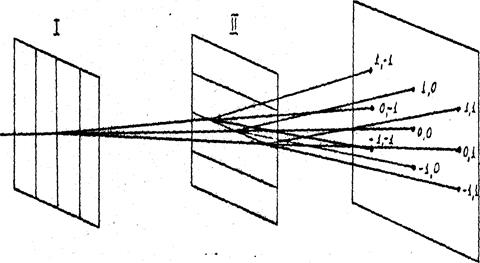
Рис. 2.2. Последовательная дифракция света на одномерных решетках 1 и 2
Из рисунка видно, что дифракционная картина представляет собой ряд упорядоченно расположенных максимумов. Цифры 0,0; 0,1; 1,1 и т.д. около максимумов показывают порядок спектра в первой и второй решётках, их интенсивность убывает по тому же закону, что и в обычной одномерной дифракционной решетке. Нетрудно вычислить положение этих максимумов, рассматривая их как результат последовательной дифракции на решётке 1 и решётке 2 рис. 2.2. Пусть свет падает на подобную решётку нормально. Выберем направление распространения падающего луча за ось Z, а направления вдоль решёток – за оси X и Y рис. 2.3. Направление падающего луча зададим углами a0, b0, g0, а дифрагированного – углами a, b, g (углы между направлением луча и соответствующей координатной осью). В нашем случае a0 = b0 = p/2, g0 = 0. Отклонение дифрагированного луча вдоль Х приведет к образованию минимумов и максимумов света в зависимости от угла дифракцииa. Используя теорию одномерной решётки из условия главных максимумов (2.1) в данном случае получаем
d1 cos a = ± n1 l (2.2)
Здесь учтено, что угол j в выражении (2.1) отсчитывается от нормали к поверхности решётки и поэтому a + j = p/2.
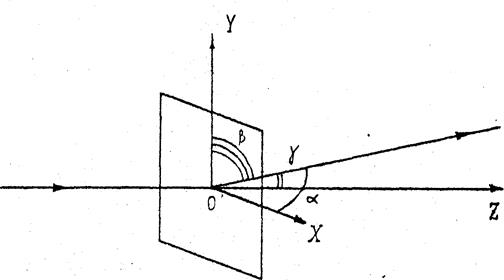 |
Рис. 2.3. Дифракция луча на одномерной решетке 1 вдоль направления X
Аналогично дифракция в направлении оси Y дает главные максимумы в направлениях, определяемых условием
d2 cos b = ± n2 l.(2.3)
Таким образом, главные максимумы возможны только в направлениях, удовлетворяющих одновременно условиям (2.2) и (2.3). Каждой паре значений n1 и n2 соответствует максимум тогоили иного порядка. Поскольку углы a, b, g – направляющие углы в декартовой системе координат, то для них должно выполняться условие
cos2 a+ cos2 b + cos2 g = 1. (2.4)
Таким образом, из трёх условий
d1 cos a = ±n1 l
d2 cos b = ± n2 l (2.5)
cos2 a+ cos2 b + cos2 g = 1
для заданной структуры с постоянными d1 и d2 и для данной длины волны l можно из (2.5) определить значения углов a, b, g, под которыми наблюдаются главные максимумы света.
На практике чаще приходится решать обратную задачу – по измеренным углам a, b, g определять значения d1 и d2 исследуемой структуры.
При изучении дифракции света удобнее бывает измерять не углы дифракции, а расстояния между максимумами на экране и расстояние от экрана до решётки.
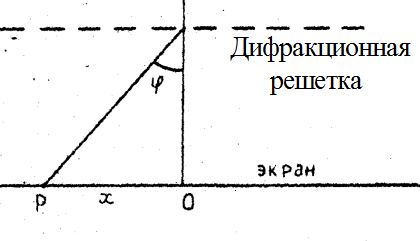
Рис. 2.4. Взаимное расположение дифракционной решетки и экрана
Из рис.2.4 видно, что
x = (x2 + ℓ2)1/2 sin j , (2.6)
где x – расстояние от центра экрана до точки наблюдения, ℓ – расстояние от экрана до решётки.
Экспериментальная часть
3.1. Приборы и принадлежности:
1) оптический квантовый генератор с блоком питания;
2) оптическая скамья с экраном для наблюдения;
3) мелкая сетка в держателе, используемая как двумерная дифракционная решётка.
Описание установки
Основой установки является оптическая скамья со шкалой, на одном конце которой установлен в специальном держателе оптический квантовый генератор (лазер), служащий источником монохроматического излучения. На противоположном конце скамьи установлен экран с делениями, на котором наблюдается дифракционная картина. Между экраном и оптическим квантовым генератором на скамью устанавливается в держателе мелкая сетка.
Требования по технике безопасности
При выполнении работы необходимо:
1) внимательно ознакомиться с заданием и оборудованием;
2) проверить заземление лабораторной установки и изоляцию токоведущих проводов, о замеченных неисправностях немедленно сообщить преподавателю;
3) не направлять луч лазера в глаза;
4) не загромождать рабочее место посторонними предметами;
5) по окончании работы выключить установку, отсоединить токоведущие провода от электрощитка, и привести в порядок рабочее место.
Порядок выполнения работы
1) установить на оптическую скамью перпендикулярно лазерному лучу держатель с мелкой сеткой;
2) получить на экране отчетливую дифракционную картину в виде упорядоченно расположенных пятен и измерить расстояние от сетки до экрана;
3) положив на экран листок клетчатой бумаги, зарисовать полученную картину; выделив центральный максимум и горизонтальное и вертикальное направления;
4) обозначить около каждого максимума его индексы (nx, ny) в соответствие с рис. 3.1.
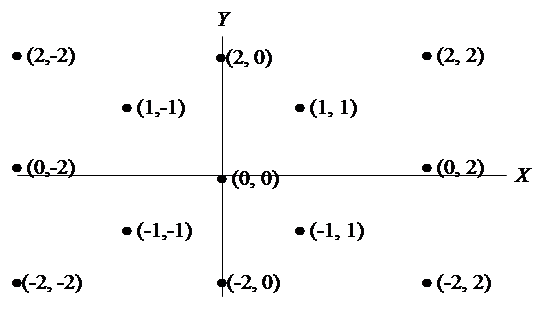 |
Рис. 3.1. Порядок обозначений главных максимумов
Индекс nx равен порядку дифракционного максимума решётки, щели которой расположены вдоль оси Х (горизонтально), индекс ny – вдоль оси Y (вертикально);
5) измерить расстояние между центральным максимумом (0,0) и максимумами, расположенными вдоль горизонтальной оси X, проходящей через центральный максимум: х01, х02, х0-1, х0-2 и т.д. для двух–трёх наблюдаемых максимумов в каждую сторону от центрального. Для максимумов вдоль оси X условия (2.5) преобразуются к виду рис. 3.2.
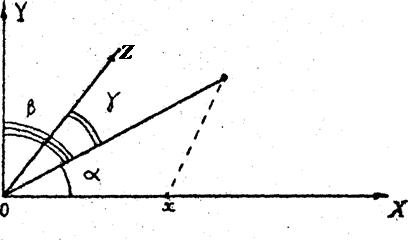 |
Рис. 3.2. Максимумы расположены вдоль оси X
a + g = p/2, или cos a = sin g,
b = p/2, z = ℓ d1 cos a = d1 sin g = ny l
sin g = x / (x2 + ℓ2) -1/2
d1 = ny l (x2 + ℓ2)1/2/ x , (3.1)
где d1 = dy – постоянная дифракционной решётки, щели которой расположены вдоль оси – Y, l – длина волны света, ℓ – расстояние от решётки до экрана;
6) вычислить dy по формуле (3.1) для различных значений ny. Данные записать в табл. 3.1.
В работе используется гелий – неоновый лазер, длина волны излучения которого l = 632,8 нм. Рассчитать среднее значение dy средн. и погрешность его определения;
7) измерить расстояние между центральным максимумом (0,0) и максимумами, расположенными вдоль вертикальной оси Y, проходящей через центральный максимум: y0, y02, y0-1, y0-2 и т. д. для двух–трёх наблюдаемых максимумов в каждую сторону от центрального. Для максимумов вдоль оси Y условия (2.5) преобразуются к виду рис 3.3.
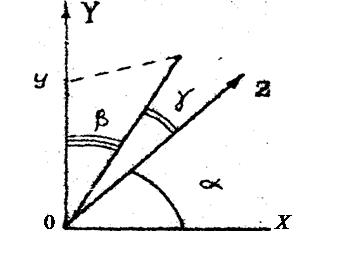 |
Рис. 3.3. Максимумы расположены вдоль оси Y
b + g = p/2, откуда cos b = sin g, a = p/2,
d2 cos b = d2 sin g = nx l,
sin g = y / (y2 + ℓ2) -1/2,
d2 = nx l (y2 + ℓ2)1/2/ y , (3.2)
где d2 = dx – постоянная дифракционной решётки, щели которой расположены вдоль оси Х;
8) вычислить dx по формуле (3.2) для различных значений nx. Данные занести в табл. 3.2.
Рассчитать среднее значение dx и погрешность его определения;
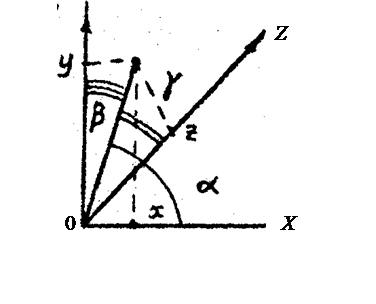 9) измерить координатыx и y максимумов, не лежащих на осях X или Y рис. 3.1. Для этих максимумов условия (2.5) будут иметь вид рис. 3.4.
9) измерить координатыx и y максимумов, не лежащих на осях X или Y рис. 3.1. Для этих максимумов условия (2.5) будут иметь вид рис. 3.4.
Рис. 3.4. Максимумы расположены между осями Х и Y
z = ℓ,
cos a = x / (x2 + y2 + z2)-1/2,
cos b = y / (x2 + y2 + z2)-1/2,
cos g = z / (x2 + y2 + z2)-1/2,
d1 cos a = ny l ® dy = ny l (x2 + y2 + z2)1/2 / x, (3.3)
d2 cos b = nx l ® dx = nx l (x2 + y2 + z2)1/2 / y; (3.4)
10) вычислить dx и dy по формулам (3.3) и (3.4) для четырех–пяти точек. Данные занести в табл. 3.3.
Рассчитать средние значения dx и dy и погрешности их определения. Сравнить эти значения с полученными ранее.
Таблица 3.1. Главные максимумы вдоль оси X
| ny | x | ℓ | dy | dy средн. |
| –1 | ||||
| –2 | ||||
| –3 |
Таблица 3.2. Главные максимумы вдоль оси Y
| nx | y | ℓ | dx | dx средн. |
| –1 | ||||
| –2 | ||||
| –3 |
Таблица 3.3. Главные максимумы, расположенные вне осей X и Y
| nx | ny | x | y | ℓ | dx | dy | dx средн. | dy средн. |
| –1 | ||||||||
| –1 | ||||||||
| –1 | –1 |
Требования к отчету
Отчет по лабораторной работе должен содержать:
1) номер, название и цель работы;
2) основные положения теории метода и расчетные формулы;
3) схему установки;
4) результаты измерений и расчетов;
5) выводы по итогам работы.
Контрольные вопросы
1. В чём заключается явление дифракции света?
2. Объясните дифракцию света на основе Принципа Гюйгенса-Френеля.
3. Объясните качественно вид дифракционной картины, даваемой двумерной дифракционной решеткой.
4. Запишите условие главных максимумов для одномерной и двумерной дифракционной решетки.
Список литературы
1. Сивухин Д.В. Общий курс физики. Оптика. –М.: Наука, 1980.
2. Детлаф А.А., Яворский Б.М. Курс физики. –М.: Высшая школа. 2000. С. 436–449.
3. Ландсберг Г.С. Оптика. –К.; Наука, 1976. С. 224–227.
4. Лабораторные занятия по физике. Под ред. Гольдина Л.Л. – М.: Наука, 1983. С. 462–476.
