Где T — период волны, dP — мощность, переносимая волной через площадку dS.

11, Волнова́я фу́нкция, или пси-функция 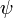— комплекснозначная функция, используемая в квантовой механике для описания чистого состояния системы. Является коэффициентом разложения вектора состояния по базису (обычно координатному):

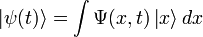
В координатном представлении волновая функция 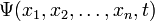зависит от координат (или обобщённых координат) системы. Физический смысл приписывается квадрату её модуля 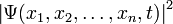, который интерпретируется как плотность вероятности 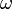(для дискретных спектров — просто вероятность) обнаружить систему в положении, описываемом координатами 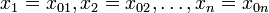в момент времени :

.

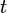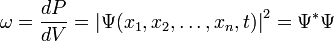Тогда в заданном квантовом состоянии системы, описываемом волновой функцией 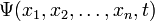, можно рассчитать вероятность 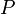того, что частица будет обнаружена в любой области пространства конечного объема : .

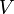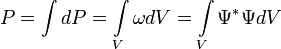
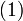Форма уравнения Шрёдингера показывает, что относительно времени его решение должно быть простым, поскольку время входит в это уравнение лишь через первую производную в правой части. Действительно, частное решение для специального случая, когда 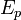не является функцией времени, можно записать в виде:

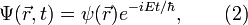
где функция 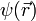должна удовлетворять уравнению:

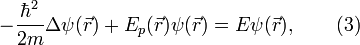
Билет 11

1, Уравнениями плоской электромагнитной волны, распространяющейся в направлении Z , являются :

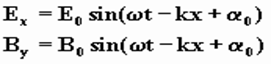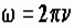где -циклическая частота, n -частота, 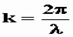-волновое число, 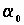-начальная фаза колебаний.

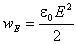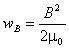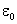2, Плотность энергии электрического поля равна а магнитного поля где и 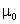– электрическая и магнитная постоянные.

3, Оптическая длина пути световой волны 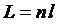,где l — геометрическая длина пути световой волны в среде с показателем преломления п.Оптическая разность хода двух световых волн .

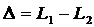4,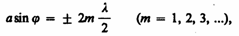

5, Закон излучения Кирхгофа —Отношение излучательной способности любого тела к его поглощательной способности одинаково для всех тел при данной температуре для данной частоты и не зависит от их формы и химической природы.

6, поле не разгоняет, а тормозит фотоэлектроны. При некотором напряжении, названном задерживающим U₃, фототок исчезает.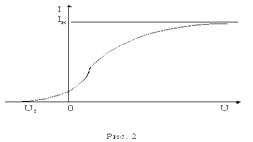

7, (n=3) s (l=0) p (l=1) d (l=2)

8, полупроводники акцепторные- это когда есть примесь в кристаллической решётке, которая отдаёт кристаллу дырку.Основные-дырки,не основные-электроны.

10, ПОЛОСЫ РАВНОЙ ТОЛЩИНЫ - интерференц. полосы, наблюдаемые при освещении тонких оптически прозрачных слоев (плёнок) переменной толщины пучком параллельных лучей и обрисовывающие линии равной оптической толщины. П. р. т. возникают, когда интерференц. картина локализована на самой плёнке. Разность хода между параллельными монохроматич. лучами, отражёнными от верхней и нижней поверхностей плёнки (рис.), равна 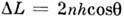(n - показатель преломления плёнки, h - её толщина, 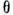- угол преломления).Ко́льца Нью́тона — кольцеобразные интерференционные максимумы и минимумы, появляющиеся вокруг точки касания слегка изогнутой выпуклой линзы и плоскопараллельной пластины при прохождении света сквозь линзу и пластину. Радиус k-го светлого кольца Ньютона (в предположении постоянного радиуса кривизны линзы) в отражённом свете выражается следующей формулой: 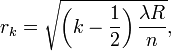R — радиус кривизны линзы;k = 2, 4, …;

λ — длина волны света в вакууме;n — показатель преломления среды между линзой и пластинкой. Радиус r_т т-го кольца определяется из треугольника А-О-С: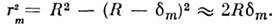

11, Корпускуля́рно-волново́й дуали́зм — принцип, согласно которому любой объект может проявлять как волновые, так и корпускулярные свойства. Был введён при разработке квантовой механики для интерпретации явлений, наблюдаемых в микромире, с точки зрения классических концепций. Дальнейшим развитием принципа корпускулярно-волнового дуализма стала концепция квантованных полей в квантовой теории поля.Основные уравнения (см. § 205), связывающие корпускулярные свойства электромагнитного излучения (энергия и импульс фотона) с волновыми свойствами (частота или длина волны):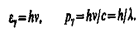

Билет 12

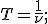
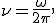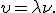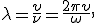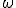1, Так как то скорость волны связана с частотой колебаний уравнением Отсюда где — циклическая частота колебани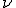й, и 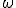зависят только от свойств источника волны.

2, 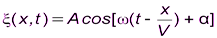или .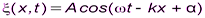

3,Если в оптической разности хода волн укладывается четное число полуволн или целое число волн, то в данной точке экрана наблюдается усиление интенсивности света (max). 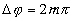, где 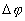- pазность фаз складываемых волн.

4, Свет со всевозможными равновероятными ориентациями вектора Е (и, следовательно, Н) называется естественным.Свет, в котором направления колебаний светового вектора каким-то образом упорядочены, называется поляризованным. Так, если в результате каких-либо внешних воздействий появляется преимущественное (но не исключительное!) направление коле­баний вектора Е (рис. 272, б),то имеем дело с частично поляризованным светом. Свет, в котором вектор Е (и, следовательно, Н) колеблется только в одном направлении, перпендикулярном лучу (рис. 272, в), называется плоско поляризованным (линейно поляризованным). Поляризованный свет отличается от естественного света своими физическими характеристиками (ориентированностью световых волн, колебания которых происходит в одной плоскости), но в обычных условиях не воспринимается визуально как какой-то особый свет. Частичная поляризация света может происходить и в результате природных процессов.

5, ЭФФЕКТ КОМПТОНА состоит в изменении длины волны, сопровождающем рассеяние пучка рентгеновских лучей в тонком слое вещества. ЭФФЕКТ КОМПТОНА состоит в изменении длины волны, сопровождающем рассеяние пучка рентгеновских лучей в тонком слое вещества. 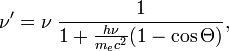где 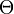— угол рассеяния (угол между направлениями распространения фотона до и после рассеяния).

Перейдя к длинам волн: 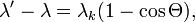где 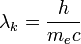— комптоновская длина волны электрона.

6, В стационарном случае уравнение Шредингера имеет вид 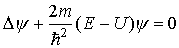где Е, U - полная и потенциальная энергия, m - масса частицы.

7, Спин электрона (и всех других микрочастиц) — квантовая величина, у нее нет классического аналога; это внутреннее неотъемлемое свойство электрона, подобное его заряду и массе.Если электрону приписывается собственный механический момент импульса (спин) Ls, то ему соответствует собственный магнитный момент рms. Согласно общим выводам квантовой механики, спин квантуется по закону 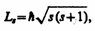где s — спиновое квантовое число.

Ядро атома состоит из положительно заряженных протонов и незаряженныхнейтронов. Если число протонов в ядре совпадает с числом электронов, то атом в целом оказывается электрически нейтральным. В противном случае он обладает некоторым положительным или отрицательным зарядом и называется ионом.

10, Луч света, проходя через плёнку толщиной 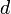, отразится дважды — от внутренней и наружной её поверхностей. Отражённые лучи будут иметь постоянную разность фаз, равную удвоенной толщине плёнки, от чего лучи становятся когерентными и будут интерферировать. Полное гашение лучей произойдет при 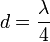, где 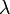— длина волны. Если 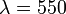нм, то толщина плёнки равняется 550:4=137,5 нм.

Лучи соседних участков спектра по обе стороны от 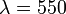нм интерферируют не полностью и только ослабляются, отчего плёнка приобретает окраску. В приближении геометрической оптики, когда есть смысл говорить об оптической разности ходалучей, для двух лучей

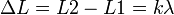— условие максимума; 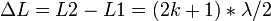— условие минимума,где k=0,1,2... и 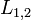— оптическая длина пути первого и второго луча, соответственно.

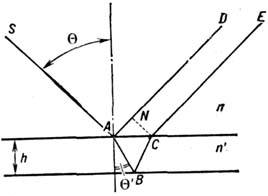
ПОЛОСЫ РАВНОГО НАКЛОНА- чередующиеся тёмные и светлые полосы (интерференционные полосы), возникающие при падении света на плоскопараллельную пластину в результате интерференции лучей, отражённых от верхней и нижней её поверхностей и выходящих параллельно друг другу. Монохроматич. свет с длиной волны 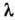от точечного источника S (рис.), находящегося в среде с показателем преломления п, падает на пластину толщиной hи с показателем преломления 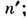при отражении луча SA от верхней и нижней граней образуются параллельные лучи AD и СЕ. Оптич. разность хода между такими лучами

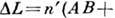
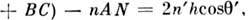а соответствующая разность фаз 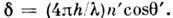С учётом сдвига фаз на

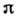при отражении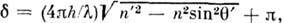

ПОЛОСЫ РАВНОЙ ТОЛЩИНЫ - интерференц. полосы, наблюдаемые при освещении тонких оптически прозрачных слоев (плёнок) переменной толщины пучком параллельных лучей и обрисовывающие линии равной оптической толщины. П. р. т. возникают, когда интерференц. картина локализована на самой плёнке. Разность хода между параллельными монохроматич. лучами, отражёнными от верхней и нижней поверхностей плёнки (рис.), равна 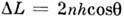(n - показатель преломления плёнки, h - её толщина, 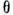- угол преломления). Учитывая изменение фазы на 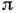при отражении от одной из поверхностей плёнки, получим, что максимумы интенсивности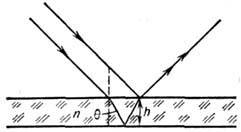

(светлые полосы) возникают при разности хода 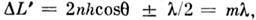m = 0,1, 2, ..., а минимумы (тёмные полосы) - при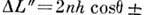

11, 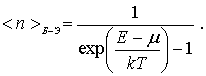распределением Бозе-Эйнштейна

Формула 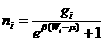называется распределением Ферми –Дирака. Функция распределения Ферми-Дирака (функция заполнения ячеек), или средняя заселенность фермионами

Энергия Фе́рми () системы невзаимодействующих фермионов — это увеличение энергии основного состояния системы при добавлении одной частицы. Это эквивалентно химическому потенциалу системы в ее основном состоянии при абсолютном нуле температур. Энергия Ферми может также интерпретироваться как максимальная энергия фермиона в основном состоянии при абсолютном нуле температур. Фермионы — частицы с полуцелым спином, обычно 1/2, такие как электроны — подчиняются принципу запрета Паули, согласно которому две одинаковые частицы не могут занимать одно и то же квантовое состояние. Следовательно, фермионы подчиняются статистике Ферми — Дирака. Бозо́н (от фамилии физика Бозе) — частица с целым значением спина. Бозоны, в отличие от фермионов, подчиняются статистике Бозе — Эйнштейна, которая допускает, чтобы в одномквантовом состоянии могло находиться неограниченное количество одинаковых частиц. Системы из многих бозонов описываются симметричными относительно перестановок частицволновыми функциями. Существенное различие классической и квантовой статистик связано с тем, что квантовая механика в отличие от классической сама является статистической теорией. Эта принципиально статистическая природа квантовой механики совершенно не зависит от специальных методов физической статистики, в которых средними значениями всегда считают результаты усреднения по различным состояниям .системы. В квантовой же механике идет речь только о средних значениях в данном фиксированном состоянии системы.

Самое существенное отличие квантовой статистики от классической связано с принципом тождественности частиц в квантовой механике. Состояние системы не изменяется при перестановке одинаковых частиц

Билет 13