Второе начало термодинамики. Теплота и работа. Первое начало термодинамики

Теплота и работа. Первое начало термодинамики

Процесс передачи внутренней энергии от одного тела к другому без совершения работы (без изменения объема) называется теплообменом. Количество энергии, передаваемое системе внешними телами при тепло-обмене, называют количеством теплоты Q.

Существует три вида теплообмена: теплопроводность, конвекция, излучение.

Теплопроводностью называется процесс теплообмена между телами при их непосредственном контакте, обусловленный хаотическим движением частиц тела.

Конвекцией называется процесс переноса энергии,которыйосуществляется перемещением слоев жидкости и газа от места с более высокой температурой к месту с более низкой температурой. Конвекция наблюдается только в жидкостях и газах.

Излучением называется перенос энергии от одного тела к другому (а также между частями одного и того же тела) путем обмена электромагнитным излучением, т. е. теплообмен, обусловленный процессами испускания , распространения , рассеяния и поглощения электро-магнитных волн.

V2	V2
A12=∫ dA =∫	pdV .

Q = U + A.

Первое начало термодинамики: теплота,сообщаемая системе,

расходуется на изменение ее внутренней энергии и на совершение ею работы против внешних сил. В дифференциальной форме первое на-чало термодинамики имеет вид:

δQ = dU + δA.

(12.1.5)

Если система периодически возвращается в первоначальное со-стояние, то изменение ее внутренней энергии равно нулю ( U = 0). Тогда согласно первому началу термодинамики A = Q, т. е. невозмо-

жен вечный двигатель первого рода −периодически действующийдвигатель, который совершал бы большую работу, чем сообщенная ему извне энергия.

Теплоемкость тела и вещества

Теплоемкостью какого−либо тела называется величина,равнаяколичеству теплоты, которое нужно сообщить телу, чтобы повысить его температуру на один Кельвин . Если при сообщении телу количе-ства теплоты dQ, его температура повышается на dT, то теплоемкость по определению равна

C = dQ .	[Дж/К]
dT

Теплоемкость моля вещества называется молярной теплоемко-стью −величина,равная количеству теплоты,необходимому для на-гревания одного моля вещества на один Кельвин:

CM =	dQ	.	[Дж/(моль · К)]
	νdT

Теплоемкость единицы массы вещества называется удельной

теплоемкостью −величина,равная количеству теплоты,необходи-мому для нагревания одного килограмма вещества на один Кельвин:

cуд=	dQ	.	[Дж/(кг · К)].
	mdT

Величина теплоемкости зависит от условий, при которых про-исходит нагревание тела. Если нагревание происходит при постоян-ном объеме, то теплоемкость называется теплоемкостью при постоянном объеме и обозначается.

CM =		dQ	и	cуд=		dQ	.	(12.2.5)
V			V
		ν dT V =const			mdT V =const

Если же нагревание происходит при постоянном давлении −

теплоемкость при постоянном давлении и обозначается

M		dQ	уд		dQ
Cp	=			и cp	=			.	(12.2.6)
		ν dT p=const		mdT p=const

Первое начало термодинамики при изохорическом, изо-барическом и изотермическом процессах.

Изохорический процесс		p	2	Нагревание
Если газ нагревается или охлаж-
дается при	постоянном	объеме
(рис.12.3.1), то dV = 0 и работа внешних	1	Охлаждение
сил равна нулю
					3
δA = pdV	⇒ A12=∫δA =0	V
	δQ = dU + δA ⇒ δQ = dU.

Для идеального газа измене-ние внутренней энергии определяется соотношением

dU =	i	νRdT .	(12.3.6)

Подставим выражение (12.3.6) в (12.3.3) и выразим C_V^M

i	ν RdT =νCM dT	CM =	i	νRdT	=	i	R .	(12.3.7)
	V	V		νdT

Удельная теплоемкость соответственно равна

	c	уд		СM	i R
		=	V =					.
	V		M	2 M

Изобарический процесс

A₁₂₌ ν R (T₂ −T₁) .

Сообщаемая газу извне теплота, согласно выражению
равна
		δQ = C pM νdT .

Изотермический процесс

Работа,

совершаемая

газом

при

изотермическом

процессе

V2

(рис. 12.3.3),

равна

A12 = ∫

pdV .

V1

V2

dV

V2

dV

V

A12=∫ν RT

V

=ν RT ∫

V

=νRT ln

.

(12.3.17)

V

V

V

Эту формулу можно преобра-

p

зовать и к иному виду, если учесть,

Изотермическое

что при изотермическом

процессе

p1

1

расширение

выполняется закон Бойля − Мариотта

p1 V1= p2 V2,откуда V2

=

p1

. Тогда

V

p

A

=νRT ln

p1

.

(12.3.18)

2

p2

p2

A12= Q12

Так как для идеального газа при T =

= const (dU = 0), то первое начало

V1

V2

V

термодинамики можно записать

в

Рис. 12.3.3

следующем виде

δQ = δA ⇒ Q

= A

=ν RT ln V2 =νRT ln

p1

.

(12.3.19)

V1

p2

5. Адиабатический процесс. Уравнение Пуассона

p

Адиабатическим

называется

Адиабата

процесс, протекающий без тепло-

обмена с окружающей средой. Оп-

ределим

уравнение, связывающее

p1

1

параметры

идеального

газа

при

адиабатическом процессе. Так как

p2

2

по условию δQ = 0, то первое нача-

ло термодинамики можно записать

A12

в следующем виде

V1

V2

V 0 =δА + dU

⇒ δA = −dU. (12.4.1)

Рис. 12.4.1

Работа

газа при

адиабатиче-

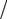
ском процессе происходит за счет убыли внутренней энергии

Политропические процессы

Про-цесс, при котором теплоемкость тела остается постоянной называется политропическим.

C = const.

Найдем уравнение политропы для идеального газа.

	ν CdT =ν C М dT + pdV .	(12.5.2)
	V
C − CpM		n lnV +ln p =const ,
		lnV + ln p = const	⇒	(12.5.8)
C − CM
	V

где n =	C − CpM
C − CM
	V

Второе начало термодинамики

1. Невозможен процесс, единственным результатом которого является передача энергии в форме теплоты от менее нагретого тела более нагретому (формулировка Клаузиуса).

2. Невозможен процесс, единственным результатом которого является превращение всей теплоты, полученной от нагревателя, в эк-

вивалентную работу (формулировка Кельвина).

Второй закон термодинамики указывает на неравноценность двух форм передачи энергии − работы и теплоты. Этот закон учиты-вает тот факт, что процесс перехода энергии упорядоченного движе-ния тела как целого (механической энергии) в энергию неупорядочен-ного движения его частиц (тепловую энергию) необратим