From (2.5) and (2.6) get the period of oscillation of the spring pendulum
ВСТУП
Основна спрямованість методичних вказівок з предмету фізика - дати можливість студентам за допомогою досліду вивчити важливі фізичні явища. Опис лабораторних робіт не претендує на те, щоб створити у студентів повне уявлення про явища, які вивчаються. Таке уявлення може виникнути лише внаслідок опрацювання лекцій та підручників.
Велика увага в методичних вказівках з фізики для студентів технічних спеціальностей приділяється обробленню результатів вимірювання. Для успішного виконання робіт необхідна попередня самостійна підготовка, в першу чергу теоретична.
Кожна лабораторна робота розрахована на дві академічні години занять у лабораторії. Перед заняттям студент повинен підготувати протокол лабораторної роботи, вивчивши відповідний теоретичний матеріал.
Під час заняття студенти проводять необхідні виміри, виконують розрахунки, доводять звіт до висновку. Результати вимірювання обговорюються з викладачем і затверджуються.
Повністю оформлений звіт по лабораторній роботі потрібно подати викладачу до кінця заняття. Він повинен містити: титульну сторінку, номер лабораторної роботи та її назву, перелік приладів і приладдя, мету роботи, схему установки, розрахункові формули, таблицю результатів вимірів і розрахунки, висновки за результатами роботи. Графіки повинні бути виконані на міліметровому папері.
Якщо студент не встигає захистити лабораторну роботу до кінця заняття, дозволяється оформити звіт (графіки) з використанням комп’ютерних програм (Excel, Origin) до наступного заняття.
Лабораторна робота вважається виконаною після успішно проведеного захисту шляхом співбесіди студента з викладачем (захист звіту + оцінка за теоретичний матеріал).
Захист звіту: мета роботи + експериментальна методика + висновки.
Теоретичний матеріал: знання фізичних явищ, які вивчалися у даній лабораторній роботі (закони, формули).
INTRODUCTION
Basic goal of the laboratory work manual on Physics is to enable students to learn important physical phenomena by experience. Laboratory work description does not try to give students a complete picture of the studied phenomena. Such presentation can only be achieved as a result of study of lectures and textbooks.
Large attention in the laboratory work manual on Physics for the students of technical professions is devoted to the handling of the measured results. Prior independent preparation, above all theoretical, is needed for successful completion of the work.
Every laboratory work is supposed to take two academic hours. Before the class a student must prepare a protocol of laboratory work and learn appropriate theoretical material.
During the class students do the necessary measurements, execute calculations and take the report to the conclusion. Measured results are discussed with a teacher and confirmed.
Fully designed report on laboratory work should be given to the teacher before the end of the class. It must include: title sheet, laboratory work number and name, list of devices and installations, purpose of work, drawing of the setting, calculation formulae, table of the measurement results and calculations, conclusions, as the result of the work. Graphs must be done on a millimeter`s paper.
If a student does not have time to support the laboratory work before the end of the class, he/she is allowed to design a report (graph) with the use of the computer programs (Excel, Origin) for the next class.
Laboratory work is considered done after the successful speech in support in front of a teacher (report explanation + mark for theoretical material).
Support of report: purpose of work + experimental method + conclusions.
Theoretical material: knowledge of the physical phenomena, which was studied in this laboratory work (laws, formulas).
ЛАБОРАТОРНА РОБОТА № 41
ПРУЖИННИЙ МАЯТНИК
Мета роботи:вивчення законів коливання пружинного маятника.
Завдання: а) визначити прискорення вільного падіння;
 б)експериментально перевірити теоретичну формулу періоду коливання пружинного маятника.
б)експериментально перевірити теоретичну формулу періоду коливання пружинного маятника.
Прилади і обладнання:пружина, комплект тягарців, секундомір, лінійка.
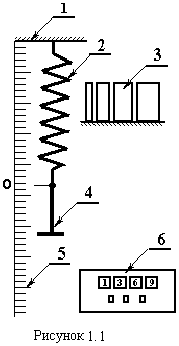
Експериментальна установка (рис.1.1) складається із кронштейна 1, на якому закріплена пружина 2 з державкою 4 та тягарців 3. Деформація пружини вимірюється лінійкою 5, а час коливань маятника – секундоміром 6.
Теоретична частина
Пружинний маятник (рис.1.2) – це тіло підвішене на пружині. При виведенні його із положення рівноваги xoна відстань x виникає сила пружності F,яка за законом Гука дорівнює F = -kx, де k– жорсткість пружини. Ця сила надає тілу прискорення
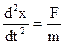 , або
, або 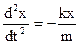 . (1.1)
. (1.1)
Рівняння (1.1) запишемо так
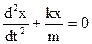 . (1.2)
. (1.2)
Позначивши 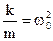 , одержуємо
, одержуємо
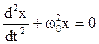 . (1.3)
. (1.3)
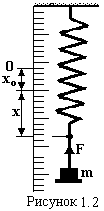 Рівняння (1.3) називається диференціальним рівнянням незатухаючих вільних гармонічних коливань. Розв’язком цього рівняння є гармонічна функція
Рівняння (1.3) називається диференціальним рівнянням незатухаючих вільних гармонічних коливань. Розв’язком цього рівняння є гармонічна функція
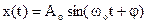 , або
, або
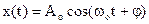 , (1.4)
, (1.4)
яка задає координату х тягарця в будь-який момент часу t.
Розглянемо характеристики гармонічних коливань.
АмплітудаАо – найбільше відхилення точки від положення рівноваги,
Циклічна частота коливань 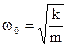 –(1.5)
–(1.5)
це кількість коливань за 2π секунд.
Період коливань 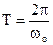 – (1.6)
– (1.6)
це час одного повного коливання, або час, за який фаза коливання змінюється на 2π.
Частотаколивань 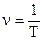 – (1.7)
– (1.7)
це кількість коливань за 1 секунду.
Із (1.5) і (1.6) отримуємо період коливань пружинного маятника
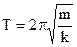 . (1.8)
. (1.8)
Коли на пружині висить тягарець, який не здійснює коливань, він деформує пружину на величину хо. За законом Гука F = mg = kxo , можна знайти жорсткість пружини 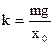 . (1.9)
. (1.9)
Тоді формула (1.8)для періоду коливань набуває виду
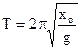 (1.10), або
(1.10), або 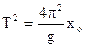 . (1.11)
. (1.11)
Таким чином, експериментально вимірюючи період коливань Т і видовження пружини хо,від її недеформованого стану до положення рівноваги при різних навантаженнях, можна по куту нахилу графіка Т2 = f(xo) (див. формулу 1.11) знайти прискорення вільного падіння. Так виконується перше завдання.
Друге завдання роботи виконується на основі формули (1.8), тобто перевіряється лінійність залежності 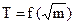 .
.
Практична частина
1. Зняти з пружини державку тягарців і відмітити по лінійці положення кінця пружини (точки підвісу державки).
2. Підвісити державку і, комбінуючи набором тягарців, змінювати загальну масу mпружинного маятника від найменшої (одна державка) до найбільшої (підвішені усі тягарці). Маса державки 11 г, маси тягарців вказані на них.
3. З вибраною масою m виміряти деформацію хопружини до положення рівноваги, а потім, надавши невеликої амплітуди (2÷3 см), виміряти секундоміром час 20 коливань. Результати вимірів занести в таблицю 1.1. Кількість комбінацій мас повинна бути не меншою 9÷10.
Таблиця 1.1
| № | m кг | Xo см | t с | T с | Т2 с2 | 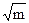 кг0,5 кг0,5 | 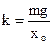 Н/м Н/м | kсер Н/м |
| - | ||||||||
| - |
4. За результатами кожного досліду розрахувати жорсткість пружини k за формулою (1.9) і знайти її середнє значення.
5. Побудувати графіки: 1) Т2 = f(xo); 2) 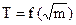
На прямолінійних частинах графіків (рис.1.3) вибрати по дві точки 1-2 і 3-4, визначити їх координати по маштабованим осям, але не із таблиці, і за формулами (1.12) та (1.13) розрахувати g і k.
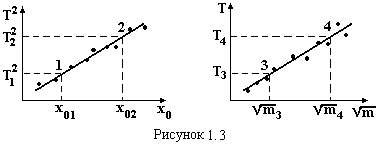 |
 (1.12)
(1.12) 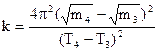 (1.13)
(1.13) 6. Зробити висновок, порівнявши значення g з табличним, а k, одержане за формулою (1.13), з середнім значенням, знайденим за формулою (1.9). У висновку також відмітити чи лінійні графіки одержано у дослідах і якщо так, то про що це свідчить?
Контрольні запитання
1. Що таке коливання?
2. Які коливання називаються гармонічними?
3. Дати визначення параметрів гармонічних коливань.
4. Одержати диференціальне рівняння незатухаючого гармонічного коливання для пружинного маятника.
5. Розв’язати диференціальне рівняння незатухаючих коливань.
6. Записати вирази для зміщення, швидкості і прискорення при незатухаючих гармонічних коливаннях та намалювати їх графіки.
7. Одержати формулу періоду незатухаючих коливань пружинного маятника.
Література
1. Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80.
2. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.195-196.
3. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.
Інструкцію склав доцент кафедри фізики ЗНТУ Манько В.К.
Laboratory work № 41
SPRING PENDULUM
Purpose of the work is to study dependence of period of oscillations on mass for a spring pendulum.
Task:to define acceleration offree falling; experimentally to check up the theoretical formula of period of the spring pendulum.
Theory
Oscillations of a spring pendulum are acted upon by the elastic force
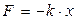 , (2.1)
, (2.1)
where x is a deviation from state of stable equilibrium, k is a rigidity of the spring. The period of oscillations is
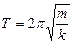 , (2.2)
, (2.2)
where m is mass of the body fixed on the spring.
Spring pendulum (fig.2.1) it a body is suspended on a spring. At the leadingout of it from position of equilibrium of xo on distance of x there is force of elasticity F, which by Hook`s law is evened F = -kx, where k is rigidity of spring. This force gives the acceleration
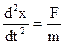 , or
, or 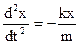 . (2.3)
. (2.3)
Equation (2.1) can be write down in such a way
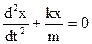 . (2.4)
. (2.4)
Designating 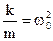 , get
, get 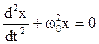 . (2.5)
. (2.5)
Equation (2.3) is named differential equation of undamped free harmonic oscillations. The decision of this equation is a harmonic function
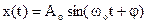 , or
, or 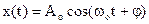 (2.6)
(2.6)
what sets the coordinate of x load in any moment of time t.
Will consider descriptions of harmonic oscillations. Amplitude of Ao is most deviation of point from position of equilibrium
Cyclic frequency of oscillations 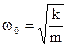 – (2.7)
– (2.7)
it is an amount of oscillations for 2π seconds.
Period of oscillations 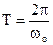 – (2.8)
– (2.8)
it is time of one full-oscillate, or time for which the phase of oscillation changes on 2π.
Frequency of oscillations 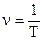 – (2.9)
– (2.9)
it is an amount of oscillations for 1 second.
From (2.5) and (2.6) get the period of oscillation of the spring pendulum
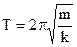 . (2.10)
. (2.10)
When load hangs on a spring, which does not carry out oscillations, it deforms a spring on the size of хо. By Hook`s law of F = mg = kxo, it is possible to find rigidity of spring
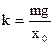 . (2.11)
. (2.11)
Then a formula (2.8) for the period of oscillations assumes an air
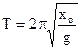 (2.12), or
(2.12), or 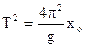 . (2.13)
. (2.13)
Thus, experimentally measuring the period of oscillations of T and lengthening of spring of хо, from its undeformed state to position of equilibrium at the different loadings, it is possible on the angle of slope of graph of T2 = f(xo) (see a formula 2.11) to find the acceleration of the free falling. The first task is so executed.
The second task of work is executed on the basis of formula (2.8), that the linearness of dependence is checked up 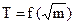 .
.
Order of execution
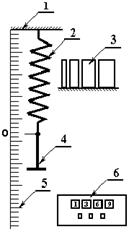
Figure 2.1
1. Varying the weights on the spring measure time of 50 oscillations by the stop-watch (once for each weight). Then calculate a period of oscillations for each measurement.
2. Represent graphically the dependence of period 
 on
on 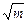 .
.
3. Using the graph determine a rigidity of the spring.
To take off from a spring fastening of loads and to mark position of end of spring on a line (points of hang up of fastening).
1. To hang up fastening and, combining the set of loads, to change general mass of m of a spring pendulum from the least (one fastening to most, all loads is suspended). Mass of fastening is 11 g, the masses of loads see on them.
2. With the chosen mass of m to measure deformation of хо spring to position of equilibrium, and then, giving small amplitude (2 ÷ 3 sm), to measure a stop-watch time 20 oscillations. To add the results of measurings to the table 2.1. An amount of combinations of the masses must be not less 9 ÷ 10.
Table 2.1
| n | m, kg | xo, sm | t, s | T, s | T2, s2 | 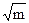 , kg0.5 , kg0.5 | 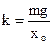 | ka |
| - | ||||||||
| - |
On results of every experience to expect rigidity of spring k on formula (2.9) and to find it mean value.
3. To build graphics: 1) Т2 = f(xo); 2) 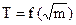
4. On lineal parts of graph (2.3) to choose for two points 1 ÷ 2 and 3 ÷ 4, to define their coordinates for to the axes, but not from a table, and after formulas (2.12) and (2.13) to expect g and k.
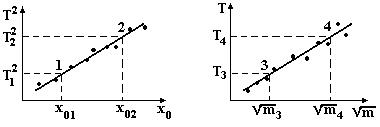
Figure 2.2
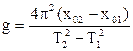 (2.14)
(2.14) 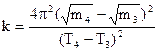 (2.15)
(2.15)
5. To draw conclusion, comparing the value of g to tabular, and k, got after a formula (2.3), with a mean value, found after a formula (2.9). In a conclusion also to mark or are line’s graphic got in experiments and if so, then what does it testify to?
Questions
1. What kind of oscillations is called harmonic? Write the dependence of deviation upon time for harmonic oscillations.
2. Give definitions for period, amplitude, frequency, cyclic frequency and phase.
3. Write the differential equation of harmonic oscillations.
4. Write the formula for period of a spring pendulum. What is a rigidity of a spring?
Translator: S.P. Lushchin, the reader, candidate of physical and mathematical sciences.
Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.
Approved by the chair of physics. Protocol № 6 from 30.03.2009 .
ЛАБОРАТОРНА РОБОТА № 42
МАТЕМАТИЧНИЙ МАЯТНИК
Мета роботи: вивчення законів коливання математичного маятни- ка.
Завдання: а) перевірити залежність періоду вільних коливань ма- тематичного маятника від довжини нитки;
б) визначити прискорення вільного падіння.
Прилади і обладнання:математичний маятник, секундомір, лі-
нійка.
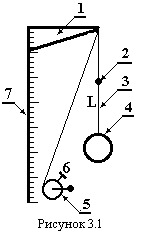 Експериментальна установка (рис.3.1) складається з кронштейна 1, через який перекинута нитка 3, на одному кінці якої прив’язана масивна куля 4, а другий кінець закріплений на котушці 5. Гумова бусинка 2 може переміщуватись по нитці і слугує для вимірювання зміни її довжини, коли куля 3 опуститься нижче лінійки 7. Довжина L нитки змінюється шляхом намотування її на котушку 5, яка фіксується стопорним гвинтом 6. Зміна довжини нитки вимірюється лінійкою 7.
Експериментальна установка (рис.3.1) складається з кронштейна 1, через який перекинута нитка 3, на одному кінці якої прив’язана масивна куля 4, а другий кінець закріплений на котушці 5. Гумова бусинка 2 може переміщуватись по нитці і слугує для вимірювання зміни її довжини, коли куля 3 опуститься нижче лінійки 7. Довжина L нитки змінюється шляхом намотування її на котушку 5, яка фіксується стопорним гвинтом 6. Зміна довжини нитки вимірюється лінійкою 7.
Теоретична частина
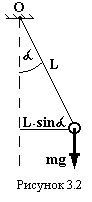
Математичний маятник – це тіло масою m, яке можна вважати матеріальною точкою, підвішене на невагомій нерозтягуваній нитці. Знайдемо період коливань такого маятника. Якщо нитку відхилити від вертикального положення, виникає зворотний момент сили тяжіння mg, плече якої дорівнює L·sinα (рис.3.2). Під дією цього моменту тіло m обертається навколо точки підвісу О. Записуємо основне рівняння динаміки обертального руху
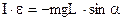 . (3.1)
. (3.1)
Тут: 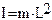 - момент інерції матеріальної точки,
- момент інерції матеріальної точки, 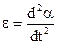 кутове прискорення. Знак мінус враховує, що момент сили mg зменшує кут α.
кутове прискорення. Знак мінус враховує, що момент сили mg зменшує кут α.
Одержуємо диференціальне рівняння незатухаючих коливань математичного маятника
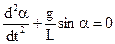 . (3.2)
. (3.2)
При малих кутах α (менших 5о) можна вважити, що sinα = α. Одержуємо 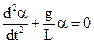 . (3.3)
. (3.3)
Порівнюючи це рівняння із загальним рівнянням незатухаючих гармонічних коливань 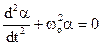 , (3.4)
, (3.4)
маємо 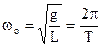 - циклічна частота коливань, Т – період коливань математичного маятника. Прийнявши L = L0 + ΔL, одержуємо
- циклічна частота коливань, Т – період коливань математичного маятника. Прийнявши L = L0 + ΔL, одержуємо
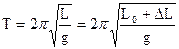 . (3.5)
. (3.5)
Піднесемо це рівняння до квадрату
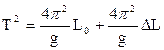 . (3.6)
. (3.6)
Видно, що залежність квадрату періоду Т2 від зміни довжини нитки ΔL за теорією повинна бути лінійною, а її нахил визначається прискоренням вільного падіння g.
Розв’язком рівняння (3.4) є рівняння незатухаючих гармонічних коливань
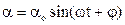 . (3.7)
. (3.7)
Практична частина
1. Відпустити стопорний гвинт 5 і встановити довжину нитки приблизно 50 см.
2. Привести маятник у коливальний рух, відхиливши його на кут не більший, ніж 5о.
3. В одному з крайніх положень маятника, який коливається, увімкнути секундомір і виміряти час 20 повних коливань. Результат записати в таблицю 3.1. Це відповідатиме значенню ΔL = 0.
Таблиця 3.1
| t, сек. | Т = t/20, сек. | Т2, сек2 | ΔL, см |
4. Замітити положення бусинки 2 по лінійці 7. Відпустити стопорний гвинт 6 і подовжити нитку на ΔL = 10 см. Подовження нитки вимірювати по переміщенню разом з нею бусинки. Закрутити стопорний гвинт.
5. Повторювати п. 2 - 5 до максимально можливої довжини нитки (до підлоги). Коли бусинка опуститься нижче лінійки, перемістити її вгору.
6. Розрахувати період Т = t/20 та його квадрат. Результат занести в таблицю 3.1.
7. 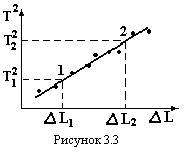 Побудувати графік залежності квадрата періоду Т2 від подовження нитки ΔL(рис.3.3). Лінійний вид цього графіка свідчить про справедливість залежності (3.5) Т ~
Побудувати графік залежності квадрата періоду Т2 від подовження нитки ΔL(рис.3.3). Лінійний вид цього графіка свідчить про справедливість залежності (3.5) Т ~ 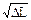 .
.
8. На прямолінійній частині графіка вибрати дві точки 1 і 2, ви
9. значити їх координати 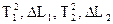 . Знайти прискорення вільного падіння за формулою:
. Знайти прискорення вільного падіння за формулою:
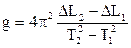 . (3.8)
. (3.8)
10. Порівняти одержане значення з табличним 9,8 м/с2. Зробити висновок.
Контрольні запитання
1. Що таке математичний маятник?
2. Складіть та запишіть диференціальне рівняння вільних гармонічних коливань математичного маятника.
3. Запишіть рівняння коливань, яке є рішенням диференціального рівняння математичного маятника. Накресліть графік цього рівняння.
4. Дати визначення величинам, які входять у рівняння коливань математичного маятника.
5. Записати формули для періоду та циклічної частоти коливань математичного маятника.
Література
1. Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80.
2. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.195-196.
3. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.
Інструкцію склав доцент каф. фізики ЗНТУ Манько В.К.
Laboratory work № 42
MATHEMATICAL PENDULUM
Purpose of work: to measure the free fall acceleration.
INSTRUMENTATION AND APPLIANCES: mathematical pendulum; the stop-watch, straightedge.
Short theory
The point mass suspended by means of an unelastic weightless thread is called the mathematical pendulum. The restoring force is the projection of the force of gravity P=mg on the direction of motion of the point mass. In this case
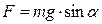 ,
,
where a = x/l, the angle between positions of l in free state and deviation state.
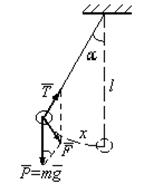
Figure 4.1
If the angles a are so small that sina » a, then
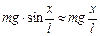 .
.
Since this force is always directed to the equilibrium position and that is why it has a sign opposite to that of x:
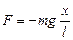
In this case the oscillations are harmonic. The second Newton’s law is
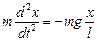 .
.
Finally we obtain the differential equation of harmonic oscillations:
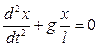 .
.
If g/l=w2, then
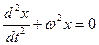 .
.
Solution of this equation is
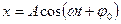
The cyclic frequency is
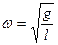 ,
,
and period is equal
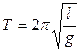 ,
,
i. e., the frequency and the period of oscillations do not depend on the mass of the oscillating body; they are determined only by the length of the thread and the free fall acceleration. The measurement of the period of a mathematical pendulum is used for determine g:
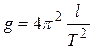 .
.
Experimental part
1. Fix the end of the cord in the first position (l = 50 cm). Make the pendulum vibrate (the amplitude of vibration must not be more than the ball diameter). Determine time of 50 oscillations by the stop-watch three times and calculate the period T using the average value of the time.
2. Determine the free fall acceleration g.
3. Calculate an error.
4. Investigate relation between the period T and the length l. Put the end of the cord in the second position (l = 150 cm). Calculate period of oscillations 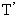 in the same way and compare with T.
in the same way and compare with T.
5. Increase the amplitude of oscillations twice. Test independence of the period on the amplitude of oscillations (small amplitude and big amplitude).
6. Make conclusions.
Control questions
1. What is a mathematical pendulum?
2. What kind of oscillations is called harmonic?
3. Write the differential equation of harmonic oscillations.
4. Write the dependence of deviation upon time for harmonic oscillations. Show this dependence in figure.
5. Give definitions for a period, an amplitude, a frequency, a cyclic frequency and a phase of vibration.
Translator: S.P. Lushchin, the reader, candidate of physical and mathematical sciences.
Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.
Approved by the chair of physics. Protocol № 6 from 30.03.2009 .
ЛАБОРАТОРНА РОБОТА № 43.1
ФІЗИЧНИЙ МАЯТНИК
Мета роботи:вивчення законів коливанняфізичного маятника.
Завдання:а) перевірити залежність періоду вільних коливань фі-зичного маятника від його моменту інерції;
б) визначити величину прискорення вільного падіння.
Прилади і обладнання: фізичний маятник, секундомір, лінійка.
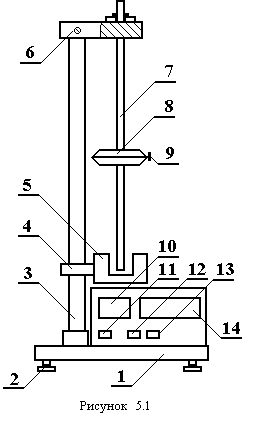 Експериментальна установка (рис.5.1) складається із основи 1, вирівнювання якої здійснюється ніжками 2. В основі закріплена стійка 3, на якій фіксується нижній кронштейн 4 з фотоелектричним датчиком 5. На верхньому кронштейні 6 підвішений фізичний маятник. Він складається зі стержня 7, вантажу 8 і фіксатора 9. На стержні 7 через 10мм зроблені кільцеві нарізки для точного визначення довжини маятника та чіткої фіксації вантажу 8. На передній панелі приладу знаходяться: індикатор кількості коливань–10, індикатор часу–14, вимикачі “СЕТЬ”–11 “СБРОС”–12 і “СТОП”–13.
Експериментальна установка (рис.5.1) складається із основи 1, вирівнювання якої здійснюється ніжками 2. В основі закріплена стійка 3, на якій фіксується нижній кронштейн 4 з фотоелектричним датчиком 5. На верхньому кронштейні 6 підвішений фізичний маятник. Він складається зі стержня 7, вантажу 8 і фіксатора 9. На стержні 7 через 10мм зроблені кільцеві нарізки для точного визначення довжини маятника та чіткої фіксації вантажу 8. На передній панелі приладу знаходяться: індикатор кількості коливань–10, індикатор часу–14, вимикачі “СЕТЬ”–11 “СБРОС”–12 і “СТОП”–13.
Під час руху маятника світловий потік від лампочки фотоелектричного датчика перекривається, що вмикає електронну схему підрахунку кількості коливань та секундомір. Після натискування вимикача “СТОП” секундомір зупиняється після закінчення поточного повного коливання.
Теоретична частина
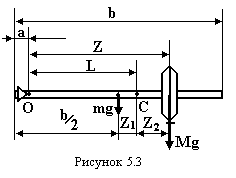
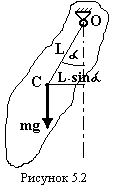 Фізичний маятник – це тіло, яке може обертатись відносно довільної горизонтальної осі, що не проходить через центр маси. Під дією моменту сили тяжіння mg, плече якої дорівнює L·sinα, тіло обертається навколо точки підвісу О (рис.5.2).L – відстань від точки О обертання (точки підвісу) до точки С - центра маси тіла. Записуємо основне рівняння динаміки обертального руху
Фізичний маятник – це тіло, яке може обертатись відносно довільної горизонтальної осі, що не проходить через центр маси. Під дією моменту сили тяжіння mg, плече якої дорівнює L·sinα, тіло обертається навколо точки підвісу О (рис.5.2).L – відстань від точки О обертання (точки підвісу) до точки С - центра маси тіла. Записуємо основне рівняння динаміки обертального руху
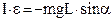 ,(5.1)
,(5.1)
I- момент інерції тіла, 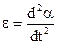 - кутове прискорення. Знак мінус враховує, що момент сили mg зменшує кут α.Таким чином, одержуємо диференціальне рівняння незатухаючих коливань фізичного маятника
- кутове прискорення. Знак мінус враховує, що момент сили mg зменшує кут α.Таким чином, одержуємо диференціальне рівняння незатухаючих коливань фізичного маятника
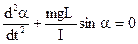 . (5.2)
. (5.2)
При малих кутах α (менших 5о) можна вважити, що sin α = α. Одержуємо 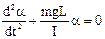 (5.3)
(5.3)
Порівнюючи одержане рівняння із загальним рівнянням незатухаючих гармонічних коливань 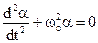 , (5.4)
, (5.4)
одержимо циклічну частоту коливань 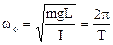 .Період коливань фізичного маятника
.Період коливань фізичного маятника
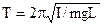 (5.5)
(5.5)
Розв’язком рівняння (5.4) є рівняння незатухаючих гармонічних коливань
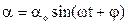 (5.6)
(5.6)
 Для виконання першого пункту завдання необхідно змінювати момент інерції маятника. Це здійснюється шляхом переміщення вантажу 8 вздовж стержня 7 (рис.5.1). Але при цьому змінюється і положення центра маси, тобто відстань L, що також необхідно врахувати.
Для виконання першого пункту завдання необхідно змінювати момент інерції маятника. Це здійснюється шляхом переміщення вантажу 8 вздовж стержня 7 (рис.5.1). Але при цьому змінюється і положення центра маси, тобто відстань L, що також необхідно врахувати.
Момент інерції маятника відносно точки коливання О дорівнює сумі моменту інерції вантажу (матеріальної точки) Iвант = МZ2 і стержня. Враховуючи теорему Штейнера, маємо Iстержня = 1/12 mb2 + m(b/2 – a)2 (рис.5.3). Таким чином момент інерції маятника, як функція відстані Z від точки підвісу до центра вантажу
I = МZ2 + 1/12 mb2 + m(b/2 – a)2 (5.7)
Знайдемо положення точки С центра мас маятника, тобто відстань L як функцію Z. За правилом моментів відносно точки С (рис.5.3) маємо
mgZ1 = MgZ2 (5.8)
Із рис.5.3 видно, що L = Z – Z2, і Z1 + b/2 =L + a . (5.9)
Із рівнянь (5.8) – (5.9) знаходимо
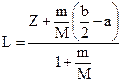 (5.10)
(5.10)
Підстановка (5.7) і (5.10) в (5.5) після піднесення (5.5) до квадрату дає
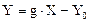 , (5.11)
, (5.11)
де 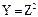 ,
, 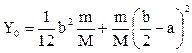 ,
,
а 
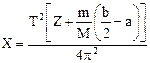 . (5.12)
. (5.12)
Таким чином, залежність Y = f(X) за теорією повинна бути лінійною. Експериментально досліджується залежність між періодом коливань Т фізичного маятника та відстанню Z вантажу до точки підвісу. Будується графік у координатах Y = f(X). Якщо одержується прямолінійний графік, то це підтверджує справедливість теоретичних формул (5.5) і (5.7), а по нахилу графіка можна розрахувати прискорення вільного падіння g. Співпадання його з табличним значенням 9,8 м/с2 кількісно підтверджує справедливість теоретичних співвідношень.
Практична частина
1. Увімкнути вилку живлення приладу в мережу 220 В і натиснути кнопку „СЕТЬ”.
2. Зняти маятник з кронштейна 6, відпустити фіксатор 9 і встановити центр вантажу 8 на відстані 10 см від точки підвісу. Відстань вимірювати кількістю видимих кільцевих нарізок на стержні від опорної призми (точки підвісу) до вантажу плюс 1 см, що враховує товщину вантажу (2 см). Добиватись чіткої фіксації вантажу в нарізках.
3. Підвісити маятник на кронштейн 6. При цьому слідкувати за надійністю його кріплення, щоб опорна призма чітко потрапила у заглиблення.
4. Відрегулювати положення кронштейна 4 так, щоб нижній кінець стержня маятника 7 не зачіпався за фотоелектричний датчик 5, але перекривав його промінь.
5. Привести маятник у коливання, відхиливши його на кут не більший, ніж 5о.
6. Після того, як маятник здійснить 1 ÷ 2 коливання, натиснути кнопку “СБРОС”. Почнеться відлік часу та кількості коливань, що буде видно на відповідних індикаторах.
7. Коли на індикаторі кількості коливань появиться цифра 9, натиснути кнопку “СТОП”. Після закінчення останнього 10-го коливання зупиниться секундомір.
8. Визначити період коливань, поділивши час на кількість коливань, тобто на 10. Відстань Z та період Т записати в таблицю 5.1.
Таблиця 5.1
| Z, см | Y = Z2, см2 | Т, сек. | Х, см×с2 |
| - | |||
| - |
9. Повторювати пп. 2 ÷ 8, кожного разу переміщувати вантаж вниз на 2 см (по дві нарізки) до найнижчого можливого положення.
10. За формулою (5.12) розрахувати Х і записати в таблицю 5.1.
11.  Параметри маятника: відношення мас m/M = 0,3; довжина верхнього кінця стержня до точки підвісу а = 5 см; загальна довжина стержня b = 59 см. Розрахунки зручніше виконувати на ЕОМ.
Параметри маятника: відношення мас m/M = 0,3; довжина верхнього кінця стержня до точки підвісу а = 5 см; загальна довжина стержня b = 59 см. Розрахунки зручніше виконувати на ЕОМ.
Побудувати графік залежності Y=f(X).
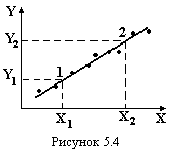
12. На прямолінійній його частині вибрати дві точки 1 і 2, (рис.5.4) визначити їх координати по осям, але не із таблиці, і знайти прискорення вільного падіння за формулою
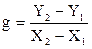 , см/с2. (5.13)
, см/с2. (5.13)
13. Порівняти одержане значення з довідковим 980 см/с2. Зробити висновок.
Контрольні запитання
1. Що таке фізичний маятник?
2. Складіть та запишіть диференціальне рівняння вільних гармонічних коливань фізичного маятника.
3. Запишіть рівняння коливань, яке є розв’язком диференціального рівняння фізичного маятника. Накресліть графік цього рівняння.
4. Як називають величини, що входять в рівняння коливань фізичного маятника. Які розмірності цих величин?
5. Запишіть формули для періоду та циклічної частоти коливань фізичного маятника.
Література
1. Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80.
2. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.196-199.
3. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.
Інструкцію склав доцент каф. фізики ЗНТУ Манько В.К.
6 LABORATORY Work № 43.1
PHYSICAL PENDULUM
Purpose of work:check the dependence of physical pendulum free oscillations period from its moment of inertia; determine the value of the free fall acceleration.
DEVICES AND EQUIPMENT: physical pendulum, stopwatch, straightedge.
The experimental setting(fig.6.1)consists of the base 1, alignment of which is carried out by legs 2. The rack is fastened in the base 3, on which the bottom supporting arm 4 is fixed with photoelectric sensor 5. On the top supporting arm 6 is suspended the physical pendulum, which includes the rod 7, weight 8 and detent 9. On the rod 7 in 10 mm collar marks are made for the exact determination of the length and exact weight 8 fixation.
On the front gage panel there are: 10 – oscillation indicator, 14 – indicator of time, switches: -11 “Сеть”, 12 “Сброс”, 13 “Стоп”.
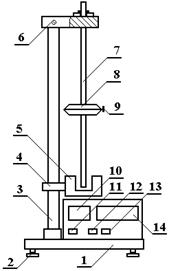
Figure 6.1
During the pendulum motion the flow of light from the lamp of the photoelectric sensor overlap and the electronic computation circuit of oscillations number and stopwatch actuates. After pressing the switch “STOP” the stopwatch stanching after the end of full current oscillations.
Theoretical part
Physical pendulum – is the solid, which can rotate relatively to the arbitrary of the horizontal axis that doesn’t pass through the center of mass. Moment of the gravity force mg, the arm of which is equal L·sin α. Value of L is the distance from pivot О (suspension center) to point С – the center of the mass of the body. Under the action of this moment the body turns round the suspension centerО.
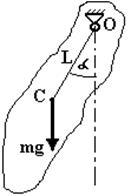
Figure 6.2
Write down the fundamental equation of the rotational motion dynamics
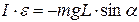 ,(6.1)
,(6.1)
where I is the moment of inertia of the body, 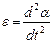 is angular acceleration, minus accounts that the moment of force of mg reduces the angle α.Thus, we get the differential equation of physical pendulum free oscillations
is angular acceleration, minus accounts that the moment of force of mg reduces the angle α.Thus, we get the differential equation of physical pendulum free oscillations
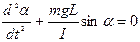 . (6.2)
. (6.2)
If angle α is small (less than 5о) we can consider that sin α = α. We get
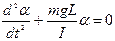 . (6.3) Comparing the received equation with the general equation of free harmonic oscillations
. (6.3) Comparing the received equation with the general equation of free harmonic oscillations
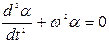 , (6.4) where
, (6.4) where 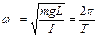 - is cyclic frequency of oscillations, Т – period. Let’s get the equation of the period of oscillations
- is cyclic frequency of oscillations, Т – period. Let’s get the equation of the period of oscillations
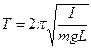 . (6.5) Equation solution (6.4) is the harmonic function which is the equation of free harmonic oscillations
. (6.5) Equation solution (6.4) is the harmonic function which is the equation of free harmonic oscillations
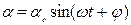 . (6.6) For performing the first task point we need to change the moment of inertia of the pendulum. It is carried out by moving the weight 8 along the rod 7. But in this way the mass center position changes, it is the distance L.
. (6.6) For performing the first task point we need to change the moment of inertia of the pendulum. It is carried out by moving the weight 8 along the rod 7. But in this way the mass center position changes, it is the distance L.
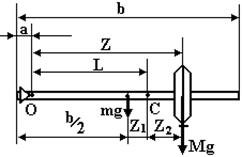
Figure 6.3
The moment of inertia of the pendulum relatively to the point О is equal to the amount of moment of inertia of the load and rod.
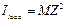
Taking into account Steiner theorem, we obtain
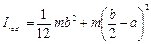 .
.
Thus, the moment of inertia of the pendulum as function of distance Z from point of suspension to weight center
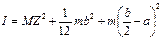 . (6.7) Let’s find the position of point С the mass center of pendulum which is the distance L as function Z. By the law of moments relatively to the point C we have:
. (6.7) Let’s find the position of point С the mass center of pendulum which is the distance L as function Z. By the law of moments relatively to the point C we have:
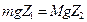 . (6.8)
. (6.8)
From figure 3 we can see that
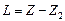 ,
, 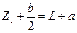 . (6.9) From equations (6.8) – (6.9) we get
. (6.9) From equations (6.8) – (6.9) we get
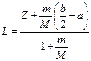 . (6.10) Substitution of (6.7) and (6.10) into (6.5) after squaring (6.5) gives us
. (6.10) Substitution of (6.7) and (6.10) into (6.5) after squaring (6.5) gives us
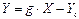 , (6.11)
, (6.11)
where
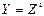 ,
,
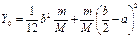 ,
,
а 
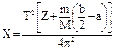 . (6.12)
. (6.12)
Thus, dependence Y = f(X) according to the theory, must be linear. Experimentally researched is the dependence of oscillations period Т of physical pendulum and distance Z from weight to suspension center. We plot the graph (6.12)
Y=f(X).
If you get a rectilinear graph, it confirms validity of theoretical formulas (6.5) and (6.7), and on its slope we can find the free fall acceleration g. Its coincidence with tabulated value 9,8 m/s2 confirms truth of the theoretical ratio.
Work procedure
1. Connect a device to the mains 220 V and push the button „Сеть”.
2. Remove the pendulum from the support arm 6, release the detent 9 and station the weight 8 center on the distance 10 сm from the suspension point. Measure the distance with the number of known collar marks on the rod from supportive prisms (suspension center) plus 1 сm to the weight which includes the thickness of the load (2 sm). Seek a clear fixing of a load in marks.
3. Hang up the pendulum on the supportive arm 6. Watch after its mounting reliability.
4. Regulate the supportive arm 4 position so that the bottom rod end of physical pendulum 7 won’t catch on photoelectric sensor 5, but block its ray.
5. Activate physical pendulum in oscillations, having rejected it on a corner less than 5о.
6. After the pendulum make 1 ÷ 2 oscillations, push the button “Сброс”. Counting of time and oscillations number will start which will be visible on corresponding indicators.
7. When oscillations indicator shows up number 9, press the button “Стоп”. The last 10-th oscillation will finish and the stopwatch will stop.
8. Define the period of oscillations, dividing time for oscillations number that is 9. Distance Z and period Т write down to the table.
9. Repeat points 2÷8, removing the weight down in 2 cm to the possibly lowest weight position.
10. Under formula (6.12) calculate Х and write it down to the table. Pendulum parameters are: mass ratio 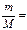 0,3; Length of the bottom rod end to suspension point а = 5 cm; total rod length b = 59 cm. Calculation it is more convenient to do on the computer.
0,3; Length of the bottom rod end to suspension point а = 5 cm; total rod length b = 59 cm. Calculation it is more convenient to do on the computer.
11. Plot the dependence Y = f(X) and choose two points 1 and 2 on its rectilinear part and define its coordinate by axes, not from the table, on the graph inclination find the free fall acceleration by the formula
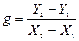 , cm/s2. (6.13) Compare the received value with reference 980 cm/s2. Write the conclusion.
, cm/s2. (6.13) Compare the received value with reference 980 cm/s2. Write the conclusion.
Table 6.1
| Z, cm | Y=Z2, cm2 | Т, s | Х, cm×s2 |
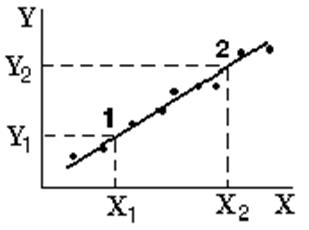
Figure 6.4
Control questions
6. What is the physical pendulum?
7. Deduce and write down the differential equation of physical pendulum’s free harmonic oscillations.
8. Write down the oscillations equation which is the solution of physical pendulum differential equation. Plot the graph of this equation.
9. What is the name of values which are a part of physical pendulum oscillations equation? What units they have?
10. Write down formulas for period and physical pendulum’s cyclic oscillation frequency.
Literature
1. Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80.
2. Савельев И.В. Курс общей физики. - т. 1, М.: Наука,1982.- С.196-199.
3. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.
Translator: S.P. Lushchin, the reader, candidate of physical and mathematical sciences.
Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.
Approved by the chair of physics. Protocol № 6 from 30.03.2009 .
ЛАБОРАТОРНА РОБОТА № 43.2
КОЛИВАННЯ СТЕРЖНЯ
Мета роботи: дослідити залежність періоду коливань стержня від відстані між віссю обертання та центром мас.
Прилади: стержень, лінійка, секундомір.
Завдання роботи:а) побудувати теоретичний та експериментальний графіки залежності періоду коливань стержня 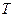 від безрозмірної довжини
від безрозмірної довжини 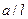 :
: 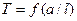 ;
;
б) знайти мінімум функції 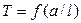 експериментальним та теоретичним шляхом.
експериментальним та теоретичним шляхом.
Теоретична частина
Коливаннями називають процеси, що повторюються з часом. Таку повторюваність мають, наприклад, рух математичного та фізичного маятників, рух струн музичних інструментів, зміна заряду та напруги на пластинах конденсатора і т. ін.
Розглянемо коливання стержня, положення осі якого можна змінювати вздовж стержня. Такий стержень уявляє собою фізичний маятник. Фізичним маятником називають тверде тіло довільної форми, що має можливість обертатись навколо горизонтальної осі під впливом сили тяжіння. Період коливань фізичного маятника визначається за формулою:
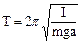 , (7.1)
, (7.1)
де I – момент інерції стержня, m – його маса, а – відстань від осі обертання до центра мас, g – прискорення вільного руху. 
Момент інерції I у даному випадку визначається за теоремою Штейнера:
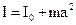 , (7.2)
, (7.2)
де 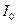 – момент інерції стержня відносно осі, що проходить перпендикулярно до стержня через його центр:
– момент інерції стержня відносно осі, що проходить перпендикулярно до стержня через його центр:
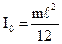 (7.3).
(7.3).
Після підстановки (7.2) і (7.3) в формулу (7.1) одержуємо:
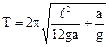 (7.4).
(7.4).
Проведемо дослідження формули (7.4). Величина а може змінюватись в інтервалі: 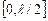 .
.
 1. При
1. При 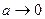 , період
, період 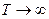 , тобто при закріпленні стержня в центрі мас він взагалі не буде коливатись, оскільки в цьому випадку сумарний момент сил тяжіння, що діють на стержень у будь-якому його положенні, дорівнюватиме нулю.
, тобто при закріпленні стержня в центрі мас він взагалі не буде коливатись, оскільки в цьому випадку сумарний момент сил тяжіння, що діють на стержень у будь-якому його положенні, дорівнюватиме нулю.
2. При 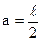 для Т одержуємо:
для Т одержуємо: 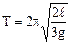 (7.5)
(7.5)
3. Дослідження формули (7.4) на наявність екстремуму показує, що функція має мінімум, координата якого знаходиться з умови: 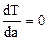 . Після диференціювання (7.4) знаходимо, що функція має мінімум при
. Після диференціювання (7.4) знаходимо, що функція має мінімум при
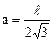 , (7.6)
, (7.6)
або приблизно при 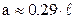 .
.
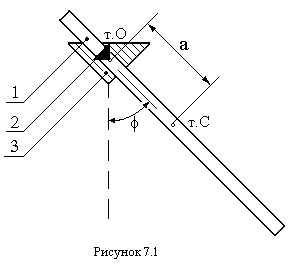
Для експериментального дослідження залежності періоду коливань стержня від положення осі обертання застосовується пристрій, зображений на рисунку 7.1. Якщо стержень 1 встановити опорною призмою 2 на кронштейн 3, вивести з положення рівноваги на деякий кут 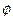 і відпустити, то він буде здійснювати коливання відносно положення рівноваги.
і відпустити, то він буде здійснювати коливання відносно положення рівноваги.
Практична частина
1. Виміряти довжину стержня 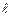 .
.
2. Встановити опорну призму 2 на першому значенні a з таблиці.
3. Встановити стержень на кронштейн 3.
4. Вивести маятник з положення рівноваги на кут 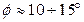 і відпустити; виміряти час 10 повних коливань. Період Т занести в таблицю 7.1.
і відпустити; виміряти час 10 повних коливань. Період Т занести в таблицю 7.1.
5. Повторити виміри з іншими значеннями а, які вказані в таблиці 7.1.
Таблиця 7.1
| n | 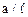 | а, см | Т, с | 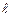 , см , см | |
| експеримент | теорія | ||||
| 0,01 | |||||
| 0,02 | |||||
| 0,03 | |||||
| 0,04 | |||||
| 0,05 | |||||
| 0,1 | |||||
| 0,2 | |||||
| 0,3 | |||||
| 0,4 | |||||
| 0,45 |
6. За формулою (7.4) розрахувати теоретичні значення періоду T. Порівняти експериментальні та теоретичні значення періоду.
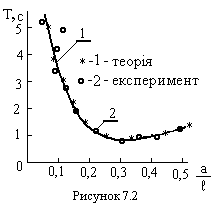
7. На одному полі (бажано на міліметровому папері) побудувати теоретичний та експериментальний графіки 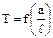 за зразком, який представлено на рис.7.2.
за зразком, який представлено на рис.7.2.
8. Знайти першу похідну функції (7.4) по параметру а. З умови 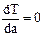 знайти теоретичне значення координати мінімуму функції; порівняти теоретичне значення з експериментальним, знайденим по графіку.
знайти теоретичне значення координати мінімуму функції; порівняти теоретичне значення з експериментальним, знайденим по графіку.
Зробити висновки.
Додатково. Побудувати теоретичний та експериментальний графіки за допомогою комп’ютера.
Для більш детального дослідження мінімуму функції (7.4) провести додаткові вимірювання періоду коливань в інтервалі а 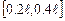 з меншим кроком (наприклад
з меншим кроком (наприклад 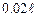 ). Розрахувати теоретичні значення періоду при тих самих значеннях
). Розрахувати теоретичні значення періоду при тих самих значеннях 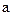 . Порівняти теорію з експериментом, побудувавши графіки. Зробити висновки, щодо справедливості формул (7.1) – (7.4).
. Порівняти теорію з експериментом, побудувавши графіки. Зробити висновки, щодо справедливості формул (7.1) – (7.4).
Контрольні запитання
1. Що таке гармонічні коливання? Записати диференціальне рівняння гармонічних коливань і його рішення.
2. Що так фізичний маятник? Вивести формулу періоду коливань фізичного маятника.
3. Сформулювати теорему Штейнера
4. Вивести формулу періоду коливань стержня..
5. Намалювати графік залежності періоду коливань стержня від відстані між віссю обертання та центром мас.
Література
1. Сивухин Д. В. Общий курс физики. – т. 1. – М.: Наука, 1980.
2. Савельев И. В. Курс общей физики.– т. 1. – М.: Наука, 1982.
Інструкцію склав доцент каф. фізики ЗНТУ Правда М.І.
LABORATORY WORK № 43.2
OSCILLATION OF PEG
Purpose of work is to probe dependence of period of oscillations of peg on distance between the axis of rotation and center of peg.
Devices: peg, straightedge, stop-watch.
